
- •6 Електростатика
- •6.1 Поняття про електричний заряд. Закон збереження заряду.
- •6.2 Взаємодія зарядів. Закон Кулона у вакуумі і в середовищі
- •6.3 Силові характеристики поля – напруженість та індукція
- •1.Силові лінії починаються на додатних і закінчуються на відємних зарядах.
- •2.Силові лінії не перетинаються.
- •3.Напруженість поля більша там, де більша щільність силових ліній.
- •6.4 Принцип суперпозиції та його застосування до розрахунку електростатичного поля
- •6.5 Потік вектора індукції. Теорема Остроградського-Гауса
- •6.6 Застосування Теореми Остроградського-Гауса до розрахунку електростатичного поля заряджених тіл
- •6.7 Робота в електростатичному полі.
- •6.8 Потенціал. Різниця потенціалів. Циркуляція вектора напруженості електростатичного поля
- •7.5 Еквіпотенціальні поверхні. Зв’язок між напруженістю і потенціалом електростатичного поля
- •7.6 Електроємність. Конденсатори. З’єднання конденсаторів
- •7.7 Енергія та густина енергії електростатичного поля
7.6 Електроємність. Конденсатори. З’єднання конденсаторів
Досліди показують, що при зарядженні провідників змінюється і їхній потенціал, причому між ними має місце лінійна залежність
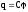 . (7.34)
. (7.34)
Коефіцієнт
пропорційності
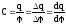 (7.35)
(7.35)
називається електроємністю провідника. Одиницею вимірювання електроємності в системі СІ є фарада (Ф). Це електроємність такого провідника, при зміні заряду якого на 1Кл його потенціал змінюється на 1В. Менші одиниці електроємності: 1мкФ = 10-6Ф, 1Нф = 10-9Ф, 1пФ = 10-12Ф.
Для
системи провідників (конденсаторів)
їхня взаємна електроємність 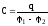 , (7.36)
, (7.36)
де
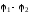 різниця потенціалів між тілами, q
– заряд одного із тіл.
різниця потенціалів між тілами, q
– заряд одного із тіл.
Знайдемо електроємності простих конденсаторів.
Приклад 1. Електроємність сфери радіусом R.
Із
(7.30) знаходимо 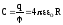 . (7.37)
. (7.37)
Приклад 2. Ємність плоского конденсатора.
Як
правило відстань між пластинами d
набагато менша від розмірів пластин.
Тому крайовими ефектами можна знехтувати
і вважати поле між пластинами однорідним.
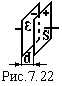
Зв'язок
між напруженістю і різницею потенціалів
для однорідного поля E
=
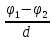 ,
,
звідки
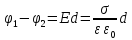 . Враховуючи, що
. Враховуючи, що
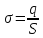 , маємо
, маємо
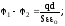
Тоді
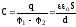 . (7.38)
. (7.38)
При з’єднанні конденсаторів у батареї загальна електроємність знаходиться так:
при
паралельному з’єднанні 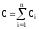 (7.41)
(7.41)
при
послідовному з’єднанні 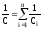 .
(7.42)
.
(7.42)
7.7 Енергія та густина енергії електростатичного поля
Для
того, щоб зарядити тіло необхідно
виконати роботу
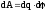 по перенесенню порції заряду dq
проти сил відштовхування від раніше
перенесеного заряду q. Ця робота
перетворюється в потенціальну енергію
зарядженого тіла (в енергію електричного
поля). Підставивши
по перенесенню порції заряду dq
проти сил відштовхування від раніше
перенесеного заряду q. Ця робота
перетворюється в потенціальну енергію
зарядженого тіла (в енергію електричного
поля). Підставивши
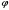 із (7.35), одержимо
із (7.35), одержимо
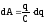 .
Інтегруємо по зарядові в інтервалі від
0 до
.
Інтегруємо по зарядові в інтервалі від
0 до
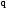 .
Врахуємо також (7.34).
.
Врахуємо також (7.34).
 .
(7.43)
.
(7.43)
Густина енергії електростатичного поля це енергія, яка зосереджена в одиниці об’єму простору, де це поле утворене
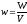 .
.
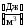 (7.44)
(7.44)
Знайдемо
її на прикладі плоского конденсатора
(див. приклад 2 розділ 7.6). Об’єм
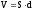 .
Із (7.38), (7.43), (7,44) і враховуючи (7.33), одержуємо
.
Із (7.38), (7.43), (7,44) і враховуючи (7.33), одержуємо
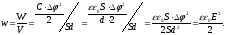
Або:
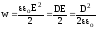 . (7.45)
. (7.45)
