
- •6 Електростатика
- •6.1 Поняття про електричний заряд. Закон збереження заряду.
- •6.2 Взаємодія зарядів. Закон Кулона у вакуумі і в середовищі
- •6.3 Силові характеристики поля – напруженість та індукція
- •1.Силові лінії починаються на додатних і закінчуються на відємних зарядах.
- •2.Силові лінії не перетинаються.
- •3.Напруженість поля більша там, де більша щільність силових ліній.
- •6.4 Принцип суперпозиції та його застосування до розрахунку електростатичного поля
- •6.5 Потік вектора індукції. Теорема Остроградського-Гауса
- •6.6 Застосування Теореми Остроградського-Гауса до розрахунку електростатичного поля заряджених тіл
- •6.7 Робота в електростатичному полі.
- •6.8 Потенціал. Різниця потенціалів. Циркуляція вектора напруженості електростатичного поля
- •7.5 Еквіпотенціальні поверхні. Зв’язок між напруженістю і потенціалом електростатичного поля
- •7.6 Електроємність. Конденсатори. З’єднання конденсаторів
- •7.7 Енергія та густина енергії електростатичного поля
1.Силові лінії починаються на додатних і закінчуються на відємних зарядах.
2.Силові лінії не перетинаються.
3.Напруженість поля більша там, де більша щільність силових ліній.
6.4 Принцип суперпозиції та його застосування до розрахунку електростатичного поля
Якщо
поле утворене декількома зарядами, то
вектор напруженості результуючого поля
знаходиться по принципу
суперпозиції:
напруженість
поля, утворена декількома зарядами
дорівнює геометричній сумі напруженостей,
утворених в даній точці кожним окремим
зарядом. 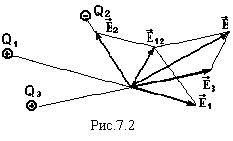
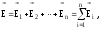
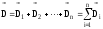 .
(6.5)
.
(6.5)
Ступінь зарядженості тіл, які не можна вважати точковими, характеризуються такими величинами:
лінійна густина заряду – заряд одиниці довжини
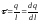

 (6.6)
(6.6)
поверхнева густина заряду – заряд одиниці площі
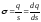

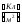 (6.7)
(6.7)
Об’ємна густина заряду – заряд одиниці об’єму
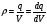

 (6.8)
(6.8)
Для полів, утворених неточковими зарядами, напруженість розраховується також по принципу суперпозиції, але формула (7.5) переходить у відповідний ( криволінійний, поверхневий чи об’ємний ) інтеграли
 ;
;
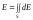
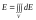 , (6.9)
, (6.9)
де
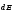 -
напруженість поля, створеного нескінченно
малим елементом тіла dl, dS чи dV. Приклади
застосування принципу суперпозиції
для розрахунку поля заряджених тіл.
-
напруженість поля, створеного нескінченно
малим елементом тіла dl, dS чи dV. Приклади
застосування принципу суперпозиції
для розрахунку поля заряджених тіл.
Приклад
1.
Розрахувати напруженість електричного
поля на осі зарядженого кільця радіусом
R, зарядом Q на відстані h від центра
кільця. 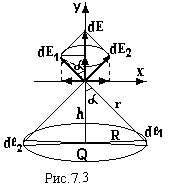
Елемент
dl1
кільця, заряд якого
 , створює напруженість поля
, створює напруженість поля
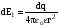 .
(6.10)
.
(6.10)
Діаметрально протилежний елемент dl2 створює напруженість dE2. Ясно, що Х–ві проекції цих векторів попарно компенсуються, а У-ві додаються.
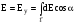 .
Враховуючи (7.10), і що
.
Враховуючи (7.10), і що
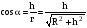 ,
одержуємо
,
одержуємо
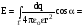
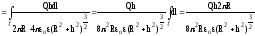
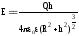 .
(6.11)
.
(6.11)
При h =0 ( в центрі кільця) Е= ?. При h → ∞ Е = 0.
6.5 Потік вектора індукції. Теорема Остроградського-Гауса
Розташуємо
в електростатичному полі з індукцією
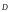 елементарну
площадку dS.
Опустимо перпендикуляр на площадку і
встановимо на ньому одиничний вектор
елементарну
площадку dS.
Опустимо перпендикуляр на площадку і
встановимо на ньому одиничний вектор
 .
Добуток
вектора
.
Добуток
вектора
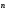 і
площі площадки dS
будемо вважати вектором площадки
і
площі площадки dS
будемо вважати вектором площадки
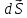 ,
який характеризує величину і орієнтацію
площадки в електростатичному полі (кут
α, див. рисунок).
,
який характеризує величину і орієнтацію
площадки в електростатичному полі (кут
α, див. рисунок).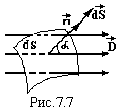
Потоком
вектора індукції
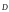 через площадку
через площадку
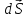 називається скалярний добуток вектора
називається скалярний добуток вектора
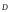 на величину площадки
на величину площадки
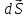 .
.
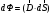 .
(6.12)
.
(6.12)
Розкриваючи скалярний добуток отримаємо
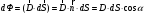 .
.
Для спрощення розрахунку полів симетричних заряджених тіл застосовується теорема Остроградського – Гауса: потік вектора електростатичної індукції через будь-яку замкнуту поверхню дорівнює алгебраїчній сумі зарядів, охоплених цією поверхнею.
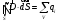 . (6.13)
. (6.13)
Якщо
заряд, наприклад, q1
знаходиться
за межами замкнутої поверхні, потік
дорівнює нулю. Дійсно, скільки силових
ліній входить в об’єм, обмежений
поверхнею, стільки ж і виходить. Силові
ж лінії від заряду q2,
який знаходиться всередині поверхні,
тільки виходять з неї.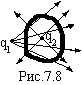
6.6 Застосування Теореми Остроградського-Гауса до розрахунку електростатичного поля заряджених тіл
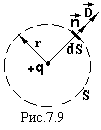
Розглянемо приклади застосування цієї теореми.
Приклад 1. Напруженість поля точкового заряду.
Поверхню S вибираємо у вигляді сфери радіусом r, в центрі якої знаходиться заряд q.
По теоремі Остроградського-Гауса маємо
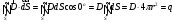

Для
різних точок сфери вектор D
однаковий
за величиною, так як всі вони однаково
розміщені по відношенню до заряду q.
Тому його винесли за знак інтегралу. А
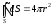 дає
площу поверхні сфери. Одержуємо
дає
площу поверхні сфери. Одержуємо
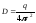 і
і
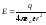 . (6.14)
. (6.14)
Приклад
2.
Поле зарядженої по поверхні до заряду
q
металевої кулі радіусом R.
Для
r
< R
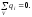 Тому D
= 0
і Е = 0. Поле всередині провідників
відсутнє. При r
> R
аналогічно прикладу 1,
Тому D
= 0
і Е = 0. Поле всередині провідників
відсутнє. При r
> R
аналогічно прикладу 1,
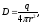 і
і
 .
(6.15)
.
(6.15)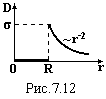
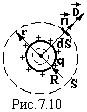
Графік залежності індукції D від радіуса r показаний на рисунку. На поверхні кулі індукція зазнає стрибкоподібної зміни на величину σ поверхневої густини вільних зарядів.
Приклад 3. Поле нескінченної зарядженої площини з поверхневою густиною заряду σ.
Поверхню
S
вибираємо у вигляді циліндра, основи
якого радіусом r
паралельні площині. Для бічної поверхні
кут між
 і
і
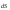 дорівнює 90о.
Тому потік через бічну поверхню дорівнює
нулю. Для елементів
дорівнює 90о.
Тому потік через бічну поверхню дорівнює
нулю. Для елементів
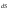 основ цей кут дорівнює 0о.
Отже можна записати
основ цей кут дорівнює 0о.
Отже можна записати
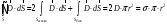
Одержуємо
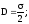
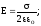 (7.16).
(7.16).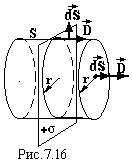
Приклад
4.
Поле нескінченних паралельних різнойменно
заряджених площин до густини зарядів
+σ і –σ.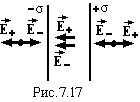
По
принципу суперпозиції
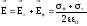 .
Якщо густини зарядів однакові, то за
межами площин
.
Якщо густини зарядів однакові, то за
межами площин

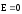 ,
а між площинами
,
а між площинами
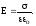 (7.17)
(7.17)
