Упражнения.

1. Дайте прямое описание непрерывных отображений стрелки в стрелку.

2. Пусть - отображение множества неотрицательных чисел в , определяемое

формулой

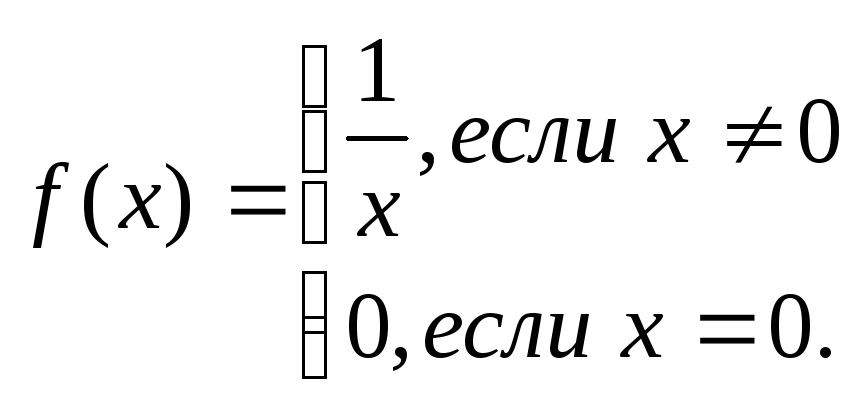
и пусть – его подотображение. Снабдим и топологией, индуцированной топологией прямой. Непрерывны ли отображение и отображение, обратное к отображению ?

3. Доказать, что если - последовательность непрерывных отображений и fn равномерно сходятся к (-метрическое пространство), то непрерывно.

4. Доказать, что любое сжимающее отображение метрического пространства непрерывно.

5. Постройте пример непрерывной биекции, не являющейся гомеоморфизмом.

6. Постройте непрерывную биекцию , не являющуюся гомеоморфизмом.

7. Пусть - гомеоморфизм. Докажите, что открыто (в ) тогда и только тогда, когда открыто (в ).

8. Доказать, что - гомеоморфизм тогда и только тогда, когда - биекция и определяет биекцию между топологическими структурами пространств и .

9. Пусть - гомеоморфизм. Докажите, что для любого :

а) замкнуто в тогда и только тогда, когда замкнуто в ;

б) ;

в) ;

г) ;

д) есть окрестность точки тогда и только тогда, когда - окрестность точки .

10. Докажите, что всякое невырожденное аффинное преобразование пространства

является гомеоморфизмом.

11. Докажите, что биекция является гомеоморфизмом тогда и только тогда, когда она монотонная функция.

12. Докажите, что любая биекция антидискретного пространства на себя является

гомеоморфизмом, и что то же самое верно для дискретного пространства и для прямой с топологией Зарисского.

13. Докажите, что любая непрерывная биекция стрелки в себя является гомеоморф-измом.

14. Постройте два гомеоморфных пространства и и непрерывную биекцию , не являющуюся гомеоморфизмом.

15. Докажите, что следующие плоские фигуры гомеоморфны:

а) вся плоскость ;

б) открытый квадрат ;

в) открытая полоса ;

г) полуплоскость ;

д) открытая полуполоса ;

е) открытый круг ;

ж) открытый прямоугольник ;

з) открытый квадрант ;

и) - плоскость с разрезом по лучу .

16. Докажите, что :

а) замкнутый круг гомеоморфен квадрату ;

б) открытый круг гомеоморфен открытому квадрату ;

в) окружность гомеоморфна контуру квадрата .

17. Докажите, что

а) любое ограниченное замкнутое выпуклое множество плоскости с непустой

внутренностью гомеоморфно ;

б) любое ограниченное открытое выпуклое множемтво плоскости гомеоморфно

плоскости;

в) граница любого ограниченного выпуклого множества плоскости, имеющего

непустую внутренность, гомеоморфна окружности.

18. Докажите, что любая замкнутая несамопересекающаяся ломаная в (и в с ) гомеоморфна окружности .

19. Докажите, что кофейная чашка (с добротной ручкой) гомеоморфна бублику.

20. Поделите следующий набор предметов на классы гомеоморфных: кофейная чашка,

блюдце, стакан, ложка, вилка, нож, тарелка, монета, гвоздь, винт, болт, чайка,

шайба, шуруп, обручальное кольцо, сверло, цветочный горшок (с отверстием в

донышке ), ключ.

21. В шаровом слое (промежутке между двумя концентрическими сферами ) просверлили цилиндрическое отверстие, соединяющее граничные сферы. Докажите, что оставшаяся часть гомеоморфна шару .

22. Постройте два негомеоморфных пространства и , для которых существуют непрерывные биекции и .

23. Доказать, что эллипсоид гомеоморфен сфере .

24. Доказать, что шар и верхнее полушарие сферы гомеоморфны.

25. Гомеоморфны ли отрезок и буква Т?

26. Доказать, что интервал гомеоморфен прямой . Доказать, что любые два интервала гомеоморфны.

27. Гомеоморфны ли шар и сфера?

28. Доказать, что интервал и открытый квадрат не гомеоморфны.

29. Доказать, что лист Мебиуса не гомеоморфен прямому произведению отрезка на

окружности.

30. Доказать, что множество всех прямых на евклидовой плоскости гомеоморфно

листу Мебиуса.