
- •Властивості алгоритму:
- •Суть алгоритмізації обчислювального процесу:
- •11. Алгоритмічно нерозв’язні проблеми. Теза Черча-Тьюринга.
- •Проблема зупинки машини Тьюринга;
- •Розпізнавання виводимості в мат.Логіці та ін.
- •Псевдокод
- •Структурограми
- •17. Алгоритмічна культура (планування етапів розробки, інкапсуляція, використання та модифікація існуючих програм, документація і т.Д.).
- •Блок-схема алгоритму відділення коренів
- •Графічна інтерпретація методу половинного ділення:
- •35. Порівняти відомі Вам методи розв’язку систем лінійних рівнянь.
- •Розв’язок систем нелінійних рівнянь методом Ньютона.
- •Інтерполяція за Лагранжем
1. Етапи розв’язання задач на ЕОМ.

 Алгоритм
–
система формальних правил, що визначає
зміст
і порядок дій над вхідними даними і
проміжними результатами, необхідними
для отримання кінцевого результату при
розв’язуванні задачі.
Алгоритм
–
система формальних правил, що визначає
зміст
і порядок дій над вхідними даними і
проміжними результатами, необхідними
для отримання кінцевого результату при
розв’язуванні задачі.
Властивості алгоритму:
1.Детермінованість (визначеність)
2.Дискретність
3.Масовість
4. Результативність
Суть алгоритмізації обчислювального процесу:
-виокремлення автономних етапів обчислювального процесу;
-формальний запис змісту кожного з них;
- визначення порядку виконання виділених автономних етапів обчислювального процесу;
-перевірка правильності вибраного алгоритму для реалізації заданого методу обчислень.
10. Машина Тьюринга.
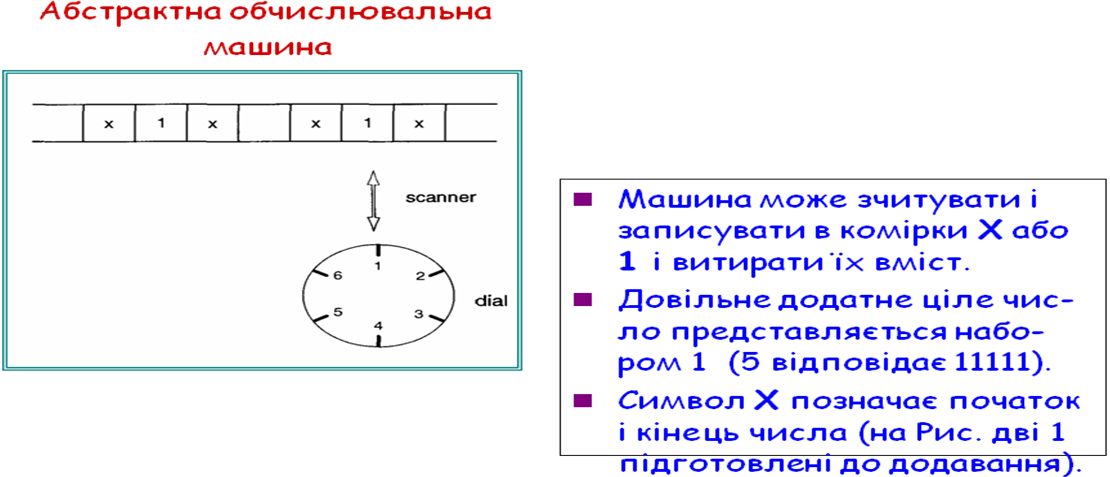
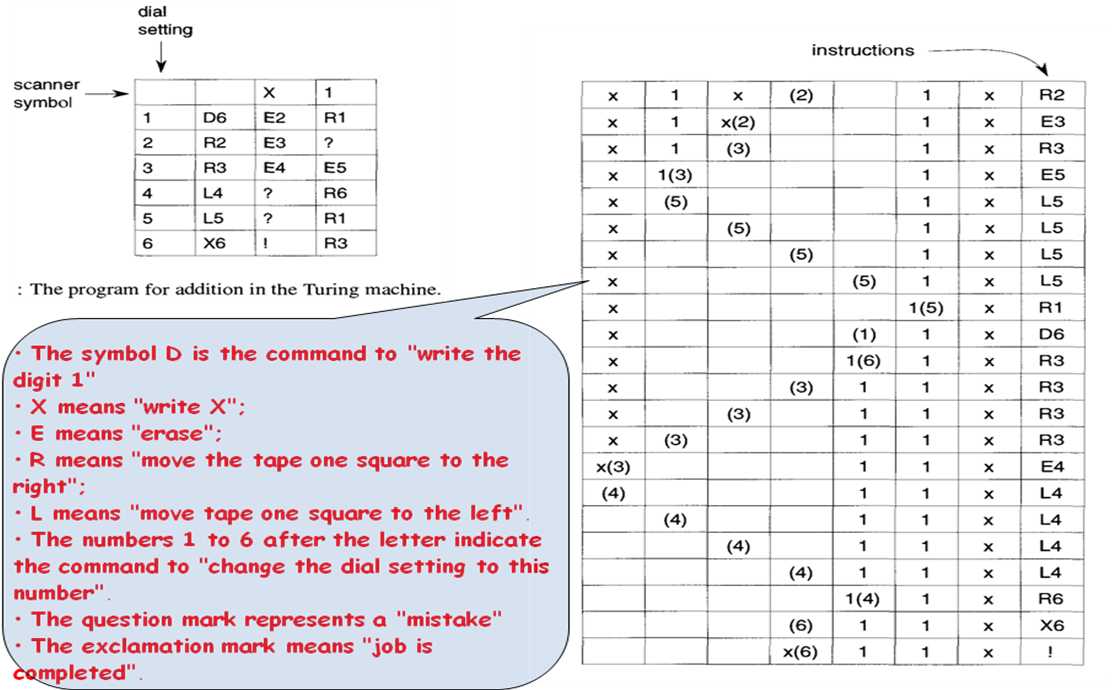
Тьюринг висловив гіпотезу про те, що для всякої обчислюваної функції можна побуду-вати машину Тьюринга. (Теза Тьюринга).
Ця теза також не може бути доведена, оскільки включає нестроге поняття обчислюваної функції.
Доведено, що клас функцій, обчислюваних за Марковим, співпадає з класом рекурсив-них функцій а, отже, з класом функцій, обчислюваних за Тьюринга.
11. Алгоритмічно нерозв’язні проблеми. Теза Черча-Тьюринга.
Якщо доведено, що дана задача не може бути розв'язана за допомогою примітивно-рекурсивних функцій, або для неї не можна побудувати нормаль-ний алгоритм Маркова, чи машину Тьюринга, то така задача називається алгоритмічно нерозв'язною.
ПРИКЛАДИ
Проблема зупинки машини Тьюринга;
Розв'язок в радикалах алгебричного рівняння n-го степеня при n > 4
Розпізнавання виводимості в мат.Логіці та ін.
Теза Черча - Тьюринга - фундаментальне евристичне твердження, істотне для багатьох галузей науки, в тому числі, для математичної логіки, теорії доказів, інформатики, кібернетики, що дає інтуїтивне поняття про вичіслімості. Це твердження було висловлено Алонзо Черчем і Аланом Тьюрингом в середині 1930-х років. У термінах теорії рекурсії, це твердження формулюється як збіг класів обчислюваних і частково рекурсивних функцій. У цьому формулюванні часто згадується як просто теза Черча. У термінах вичіслімості по Тьюрингу, теза свідчить, що для будь інтуїтивно обчислюваною функції існує обчислює її значення машина Тьюринга. Іноді в такому формулюванні фігурує як теза Тьюринга. З причини того, що класи частково обчислюваних по Тьюрингу і частково рекурсивних функцій збігаються, затвердження об'єднують у єдиний теза Черча - Тьюринга. Теза Черча - Тьюринга неможливо строго довести або спростувати, оскільки він встановлює еквівалентність між строго формалізованим поняттям частково обчислюваною функції і неформальним поняттям вичіслімості. Пізніше були сформульовані інші практичні варіанти твердження: фізичний теза Черча - Тьюринга: будь-яка функція, яка може бути обчислена фізичним пристроєм, може бути обчислена машиною Тьюринга; Сильний теза Черча - Тьюринга (теза Черча - Тьюринга - Дойча): будь-який кінцевий фізичний процес, не використовує апарат, пов'язаний з безперервністю і нескінченністю, може бути обчислений фізичним пристроєм.
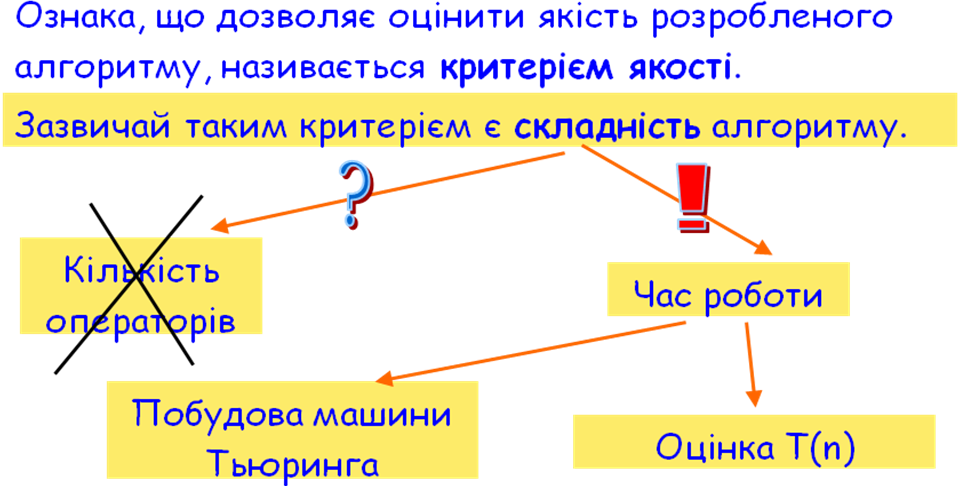
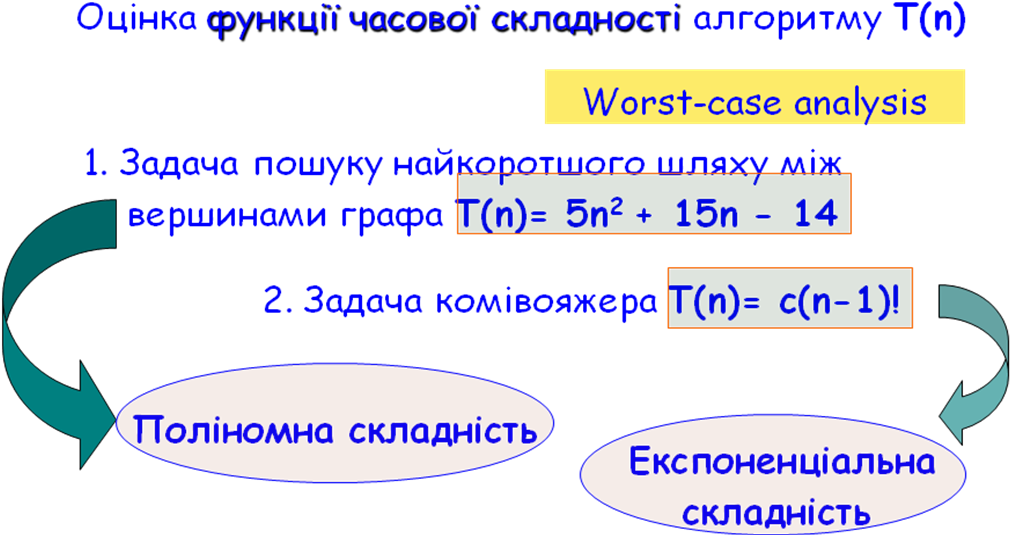
12. Складність алгоритму. Критерій складності. Оцінка функції часової складності алгоритму.
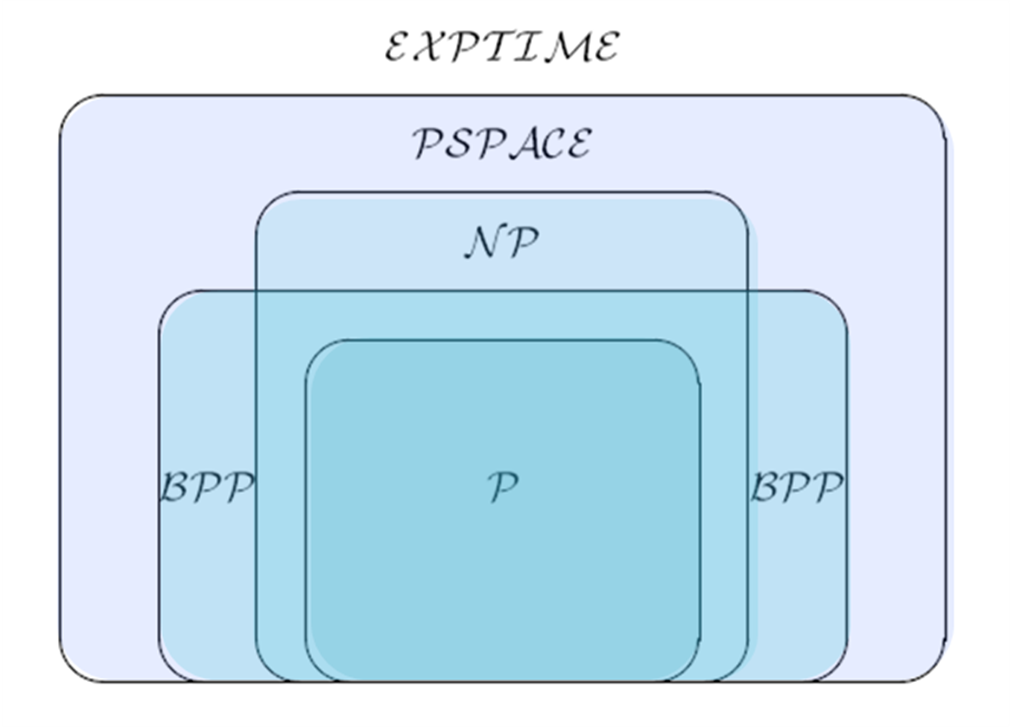
13.Класи складності алгоритмів та їх характеристика. Важкорозв’язні задачі.






14. Способи представл алгоритмів (вербальний, псевдокод, структуро грама, блок-схема).
Форми запису алгоритму:
словесна або вербальна (мовна, формульно-словесна);
псевдокод (формальні алгоритмічні мови);
схемна:
1) структурограми;
2) графічна (виконується за вимогами стандарту).
