6.3 Проектирование блока умножения чисел с фиксированной запятой

Методика проектирования блока умножения состоит из следующих основных этапов:

• составление содержательной микропрограммы выполнения операции умножения в соответствии с вариантом задания на основании анализа алгоритма умножения;

• расчет управляющей и операционной частей устройства;

• построение функциональных схем;

• составление временных диаграмм выполняемых микроопераций.

Этапы расчета, построения функциональных схем и составления временных диаграмм производятся аналогично этапам проектирования блока суммирования с фиксированной запятой на основании содержательной микропрограммы, построенной в соответствии с вариантом задания. Поэтому в данном разделе будет уделено внимание только способам (алгоритмам) умножения в прямых, обратных и дополнительных кодах.

6.3.1 Методика выполнения операции умножения над прямыми кодами исходных чисел с фиксированной запятой

Для чисел [Х]_пр = x_з, x_-1,...,x_-n, [У]_пр = y_з, y_-1, ..., y_-n ([Х]_пр, [Y]_пр<1) требуется получить [Z]_пр = [Х]_пр [У]_пр = z_з, z_-1 , z_-2, ... z_-n.

В дальнейшем, чтобы упростить написание формул, отрицательные индексы опускаются.

Операция выполняется в два этапа. Отдельно определяется знак произведения Zз в соответствии с выражением:

z_З = x_З y_З.

Затем определяется цифровая часть произведения мантисс сомножителей. Процесс умножения можно представить в следующем виде

Z = ХУ = Х(y1 + y2 + ...+ y(n-1) + y(n) ) =

= Х y1 + Х y2 + ... + Хy(n-1) + Xy(n). (6.1).

Это выражение после преобразования можно представить в виде:

Z = ((...(( 0 + Xy(n) ) + Xy(n-1) ) +... + Xy2) + Xy1) (6.2).

Полученные выражения (6.1, 6.2) являются аналитическими записями двух основных способов умножения: со старших разрядов множителя (6.1) и младших разрядов множителя (6.2).

Согласно выражению (6.2), при умножении с младших разрядов должна выполняться следующая последовательность операций:

• анализируется младшая цифра множителя. Если y_n=1, то множимое Х участвует в формировании цифровой части произведения; если yn = 0, то Х не участвует в формировании произведения;

• полученное первое частичное произведение, равное 0+Xyn, сдвигается на один разряд вправо, то есть умножается на 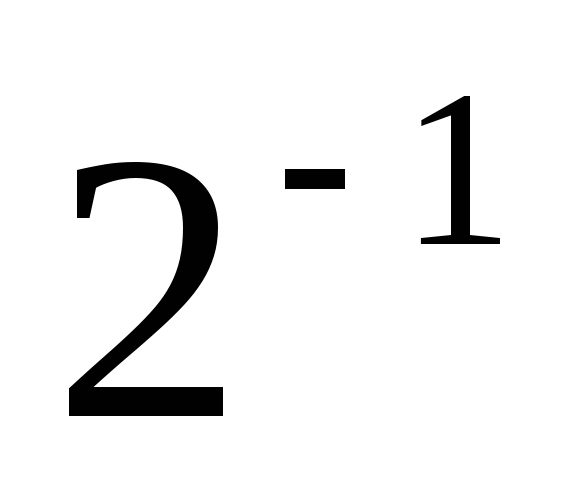. Указанная последовательность действий справедлива при умножении на все последующие разряды. Так, при умножении на разряд y_(n-1):

• анализируется цифра множителя yn-1. Если yn-1 = 1, то множимое прибавляется к сдвинутому первому частичному произведению, т.е. A2 = (0 + Xy_-n) 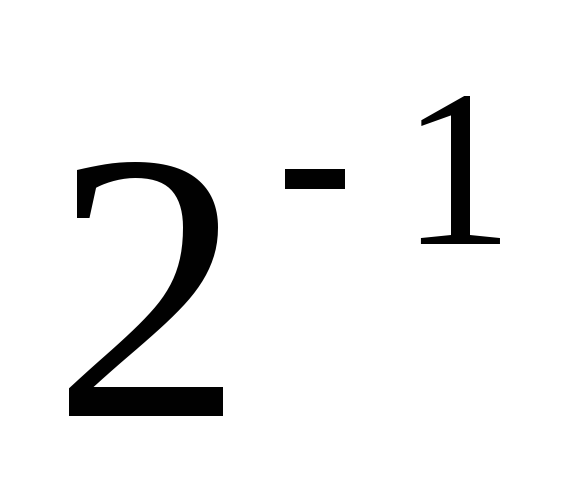+ X1 . Если yn-1=0, то множимое не участвует в формировании произведения, т.е.

A₂ = (0 + Xy_-n ) + X0;

Полученное второе частичное произведение сдвигается на один разряд вправо. Указанную процедуру умножения можно описать следующей рекуррентной формулой:

A_{( i )} = A_{( i - 1)} + y_{( n + 1- i )} Х (6.3)

Для выполнения умножения необходимо повторить n тактов ( i = 1,2,..,n) в соответствии с формулой (6.3) и в заключение осуществить последний n-й сдвиг An=XY = Z. Отметим, что при перемножении n-разрядных чисел получается 2n разрядное произведение (n-старших разрядов и n- младших). При этом получение только n старших разрядов произведения или всех 2n разрядов обеспечивается суммированием в n-разрядной сетке.

Умножение со старших разрядов множителя (6.1) при умножении только на один разряд должно выполняться в следующей последовательности:

• множимое сдвигается на 1 разряд вправо, т.е. X;

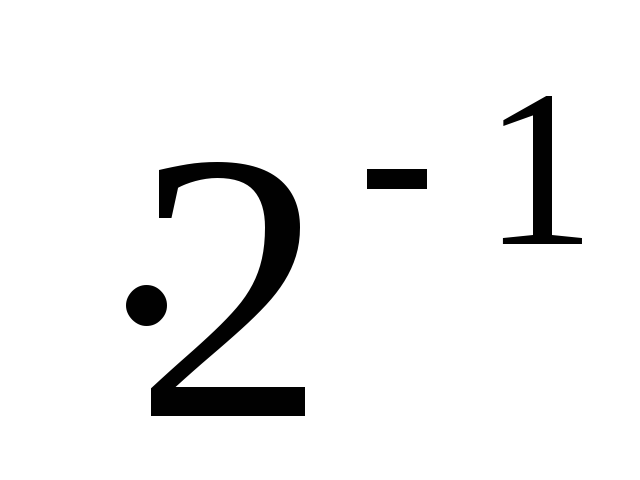• анализируется старшая цифра множителя y1. Если y_-1=1, то X 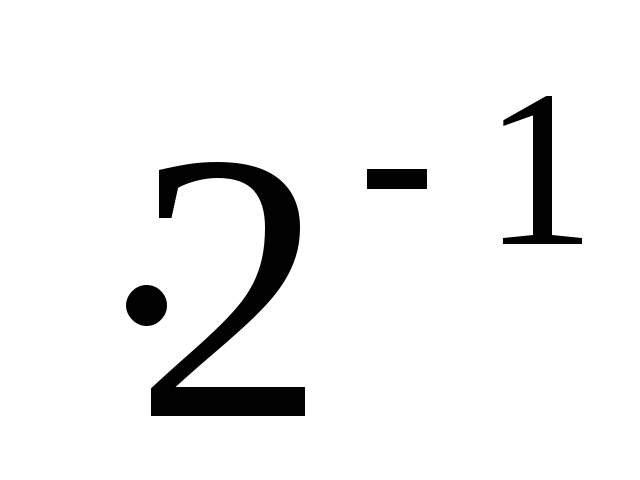участвует в формировании произведения, при y_-1 = 0, X - не участвует в формировании произведения.

Выполнение такой последовательности соответствует умножению на старший разряд множителя и справедливо при умножении на все последующие разряды. Так, при умножении на второй разряд:

• производится второй сдвиг множимого, т.е. ( X );

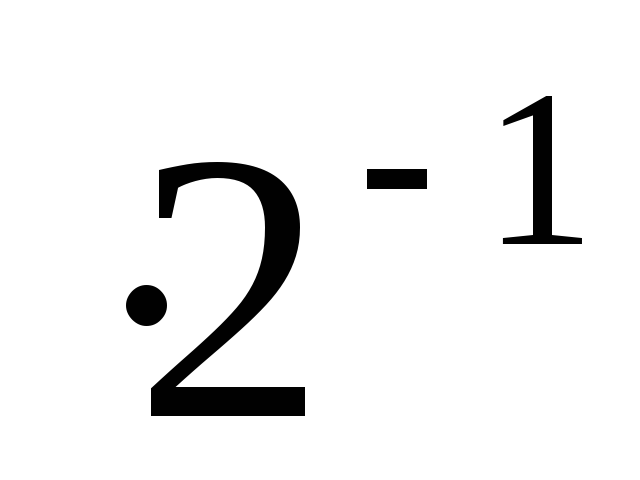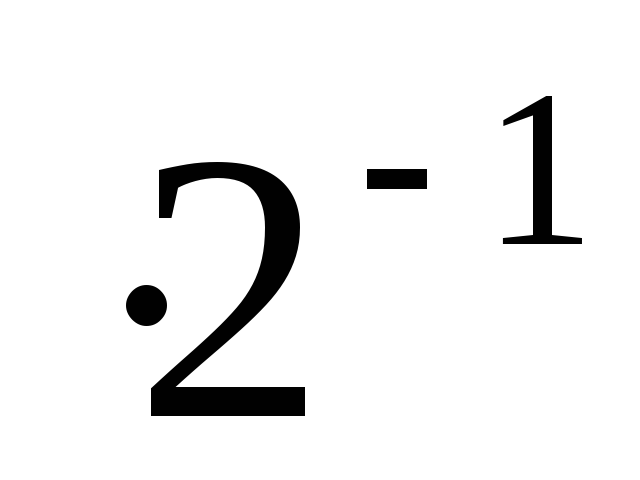• анализируется значение y2 и осуществляется или не осуществляется передача X 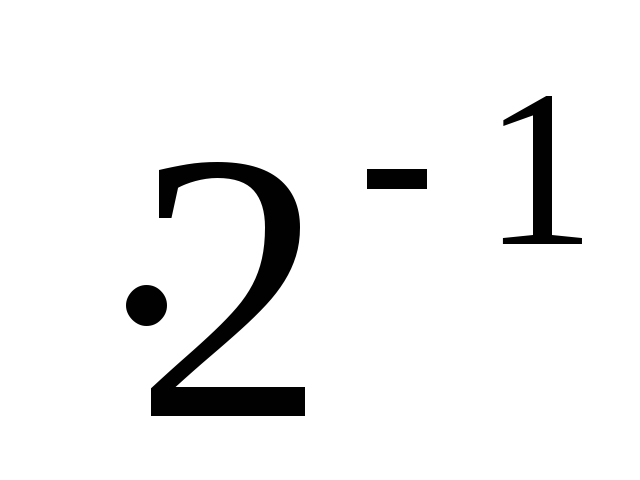на суммирование.

Процесс умножения повторяется до просмотра всех y_{(-i )} , i = 1..n.