Московский Авиационный Институт
(государственный технический университет)
«МАИ»
Факультет: Инженерно-экономический институт МАИ.
Специальность: Прикладная информатика в экономике.
Лабораторная работа №7
по дисциплине: «Эконометрика»
Тема: «Построение и исследование динамической эконометрической модели с распределенным лагом»
Студент: Мухамедьяров А.И.
Группа: 5Б - 206
Преподаватель: Виноградов С.А
Оценка: _____________
Дата: _______________
Серпухов 2012
Цель лабораторной работы: освоить методику построения модели с распределенным лагом, оценки ее параметров методом замены переменных, методом Алмона и анализ влияния факторов на выходную переменную.
Задание:
По данным таблицы 1 об объемах продаж компании 5Б-205+ за 18 последних месяцев (yt) и расходов на рекламу (xt) миллионов рублей.
Требуется:
Построить график взаимосвязи между двумя временными рядами, проанализировать экспериментальные данные на графике и приять решение о виде модели, описывающей связь yt с xt и t.
Определить параметры модели методом фиктивных переменных.
Проанализировать влияние лаговых переменных xt-p для всех p=1,..,n на результативную переменную yt. Сделать выводы.
Исходные данные
Таблица №1 – Исходные данные.
№ Месяца |
Затраты на рекламу(xt), млн. руб. |
Продажи(yt), млн. руб. |
1 |
1,52 |
17,955 |
2 |
1,23 |
16,842 |
3 |
1,78 |
18,448 |
4 |
1,45 |
18,286 |
5 |
1,48 |
17,388 |
6 |
1,12 |
16,345 |
7 |
1,34 |
15,029 |
8 |
1,38 |
15,626 |
9 |
1,45 |
16,241 |
10 |
1,14 |
16,1 |
11 |
1,58 |
17,446 |
12 |
1,45 |
17,351 |
13 |
1,24 |
16,872 |
14 |
1,35 |
16,087 |
15 |
1,68 |
17,496 |
16 |
1,65 |
18,844 |
17 |
1,56 |
18,904 |
18 |
1,5 |
19,214 |
Последовательность проведения лабораторной работы
Построить график взаимосвязи между двумя временными рядами, проанализировать экспериментальные данные на графике и приять решение о виде модели, описывающей связь yt с xt и t.
График 1 – График взаимосвязи yt, xt и t.
Анализ построенного графика показал, что изменение входной переменной xt и выходной yt имеет согласованный характер. Для оценки связей между двумя рядами xt и yt можно построить взаимно коррелируемую функцию и оценить кросс корреляцию.
Связь между переменными xt и yt:
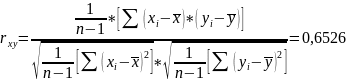
Автокорреляционная
функция первого порядка
|
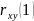
xt |
yt+1 |
xt2 |
yt+12 |
yt+1*xt |
1 |
1,52 |
16,842 |
2,3104 |
283,652964 |
25,59984 |
2 |
1,23 |
18,448 |
1,5129 |
340,328704 |
22,69104 |
3 |
1,78 |
18,286 |
3,1684 |
334,377796 |
32,54908 |
4 |
1,45 |
17,388 |
2,1025 |
302,342544 |
25,2126 |
5 |
1,48 |
16,345 |
2,1904 |
267,159025 |
24,1906 |
6 |
1,12 |
15,029 |
1,2544 |
225,870841 |
16,83248 |
7 |
1,34 |
15,626 |
1,7956 |
244,171876 |
20,93884 |
8 |
1,38 |
16,241 |
1,9044 |
263,770081 |
22,41258 |
9 |
1,45 |
16,1 |
2,1025 |
259,21 |
23,345 |
10 |
1,14 |
17,446 |
1,2996 |
304,362916 |
19,88844 |
11 |
1,58 |
17,351 |
2,4964 |
301,057201 |
27,41458 |
12 |
1,45 |
16,872 |
2,1025 |
284,664384 |
24,4644 |
13 |
1,24 |
16,087 |
1,5376 |
258,791569 |
19,94788 |
14 |
1,35 |
17,496 |
1,8225 |
306,110016 |
23,6196 |
15 |
1,68 |
18,844 |
2,8224 |
355,096336 |
31,65792 |
16 |
1,65 |
18,904 |
2,7225 |
357,361216 |
31,1916 |
17 |
1,56 |
19,214 |
2,4336 |
369,177796 |
29,97384 |
Сумма: |
24,4 |
292,519 |
35,5786 |
5057,505265 |
421,93032 |
Квадрат суммы: |
595,36 |
85567,36536 |
|
|
|
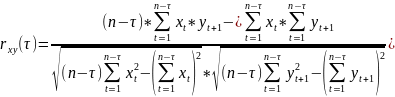
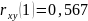
Влияние предыдущего значения xt-1 на yt присутствует, но это влияние не является очень сильным.
Автокорреляционная
функция второго порядка
|
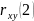
xt |
yt+2 |
xt2 |
yt+22 |
yt+2*xt |
1 |
1,52 |
18,448 |
2,3104 |
340,3287 |
28,04096 |
2 |
1,23 |
18,286 |
1,5129 |
334,3778 |
22,49178 |
3 |
1,78 |
17,388 |
3,1684 |
302,3425 |
30,95064 |
4 |
1,45 |
16,345 |
2,1025 |
267,159 |
23,70025 |
5 |
1,48 |
15,029 |
2,1904 |
225,8708 |
22,24292 |
6 |
1,12 |
15,626 |
1,2544 |
244,1719 |
17,50112 |
7 |
1,34 |
16,241 |
1,7956 |
263,7701 |
21,76294 |
8 |
1,38 |
16,1 |
1,9044 |
259,21 |
22,218 |
9 |
1,45 |
17,446 |
2,1025 |
304,3629 |
25,2967 |
10 |
1,14 |
17,351 |
1,2996 |
301,0572 |
19,78014 |
11 |
1,58 |
16,872 |
2,4964 |
284,6644 |
26,65776 |
12 |
1,45 |
16,087 |
2,1025 |
258,7916 |
23,32615 |
13 |
1,24 |
17,496 |
1,5376 |
306,11 |
21,69504 |
14 |
1,35 |
18,844 |
1,8225 |
355,0963 |
25,4394 |
15 |
1,68 |
18,904 |
2,8224 |
357,3612 |
31,75872 |
16 |
1,65 |
19,214 |
2,7225 |
369,1778 |
31,7031 |
Сумма: |
22,84 |
275,677 |
33,145 |
4773,852 |
394,5656 |
Квадрат суммы: |
521,6656 |
75997,80833 |
|
|
|
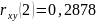
Влияние значения xt-2 на yt присутствует, но это влияние является слабым, оно еще слабее влияет на результативный признак yt ,чем xt-1.
Автокорреляционная
функция третьего порядка
|
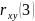
xt |
yt+3 |
xt2 |
yt+32 |
yt+3*xt |
1 |
1,52 |
18,286 |
2,3104 |
334,377796 |
27,79472 |
2 |
1,23 |
17,388 |
1,5129 |
302,342544 |
21,38724 |
3 |
1,78 |
16,345 |
3,1684 |
267,159025 |
29,0941 |
4 |
1,45 |
15,029 |
2,1025 |
225,870841 |
21,79205 |
5 |
1,48 |
15,626 |
2,1904 |
244,171876 |
23,12648 |
6 |
1,12 |
16,241 |
1,2544 |
263,770081 |
18,18992 |
7 |
1,34 |
16,1 |
1,7956 |
259,21 |
21,574 |
8 |
1,38 |
17,446 |
1,9044 |
304,362916 |
24,07548 |
9 |
1,45 |
17,351 |
2,1025 |
301,057201 |
25,15895 |
10 |
1,14 |
16,872 |
1,2996 |
284,664384 |
19,23408 |
11 |
1,58 |
16,087 |
2,4964 |
258,791569 |
25,41746 |
12 |
1,45 |
17,496 |
2,1025 |
306,110016 |
25,3692 |
13 |
1,24 |
18,844 |
1,5376 |
355,096336 |
23,36656 |
14 |
1,35 |
18,904 |
1,8225 |
357,361216 |
25,5204 |
15 |
1,68 |
19,214 |
2,8224 |
369,177796 |
32,27952 |
Сумма: |
21,19 |
257,229 |
30,4225 |
4433,523597 |
363,3802 |
Квадрат суммы: |
449,0161 |
66166,75844 |
|
|
|
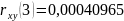
Влияние значения xt-3 на yt присутствует, но это влияние является столь слабым, что его можно не учитывать. Влияние предыдущих значений xt на переменную yt с увеличением лага уменьшается.
По результатам анализа прижимаем решение:
Использовать модель с лаговыми переменными.
Величина лага 3, p=3.