Теоретичні основи електротехніки та вимірювання

1.1. Миттєве, діюче і середнє значення синусоїдальних величин.

Синусоїдний змінний струм описується виразом

/2.2/

де і - миттєве значення струму, тобто вивчення струму в будь-який момент часу; I_m - амплітудне або максимальне значення; (2/T+) -фаза коливань; 2/T - кутова частота, яка визначав швидкість зміни фази, вимірюється в радіанах за секунду [рад/с]; - значення фази при t = 0 /початкова фаза/.

Враховуючи /2.1/, дістаємо

/2.3/

Якщо дві синусоїдні функції мають різні початкові фази, то говорять, що вони зсунуті одна відносно одної за фазою на кут

/2.4/

Якщо >0, то напруга випереджує струм або струм відстав за фазою від напруги.

Якщо початкові фази двох синусоїд однакові / /, то говорять, що напруга та струм співпадають за фазою, а якщо , тобто синусоїди зсунуті за фазою на половину періоду то говорять, що ці синусоїди знаходяться в протифазі.

Діюче значення змінного струму

Змінні струми в загальному випадку можуть значно відрізнятися за частотою і формою. Необхідне введення відповідного критерію, який міг би кількісно характеризувати дію змінного струму. Таким критерієм звичайно вважають теплову дію струму, а величину, яка характеризує цю дію, називають діючим значенням змінного струму.

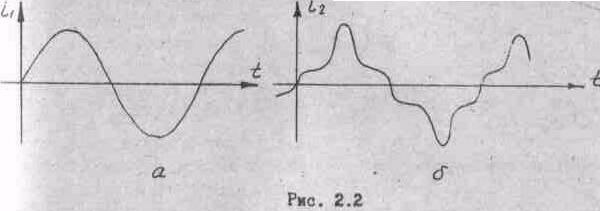
Діюче значення змінного струму дорівнює такому постійному струмові, який, протікаючи через опір r за період T, виділяє стільки ж енергії, що і змінний струм.

Звідси діюче значення змінного струму

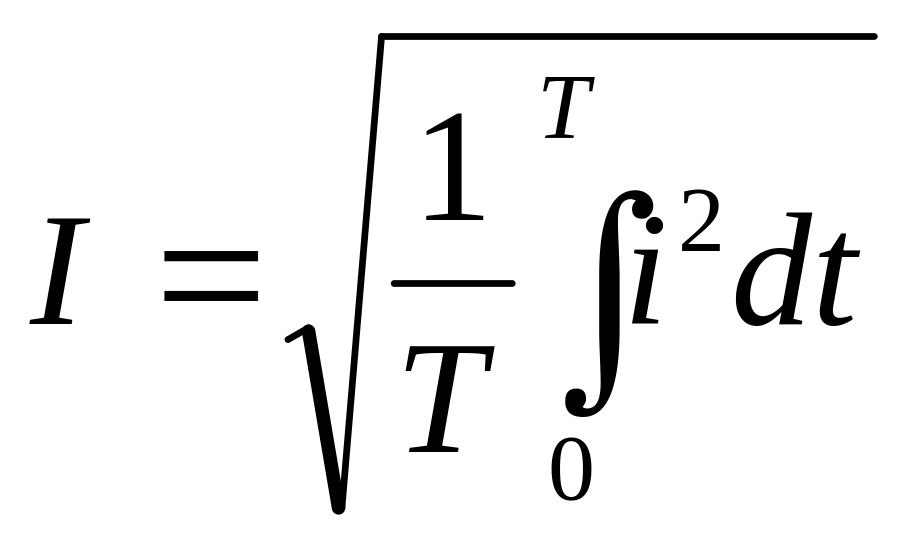/2.7/

Для змінного синусоїдного струму

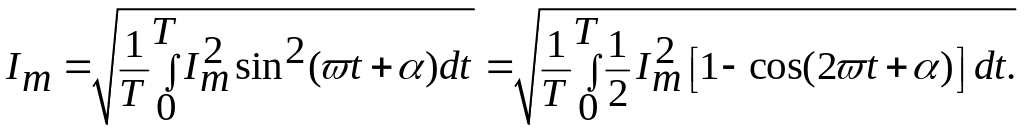
Після перетворень

/2.8/

Можна показати, що діючі значення синусоїдної напруги або ЕРС дорівнюють:

/2.9/

1.2. Представлення синусоїдальних величин комплексними числами.

Графічне зображення синусоїдних функцій /див. рис. 2.1/ звичайно називають хвильовою діорамою. Якщо на одній діаграмі зображено більш як дві синусоїдні функції, втрачається наочність і важко здійснювати графічне складання двох або більша функцій. Тому вдають­ся до зображення синусоїдних функцій векторними величинами, що знач­но покращує наочність і спрощує операцію додавання.

Нехай маємо синусоїдний струм

.

В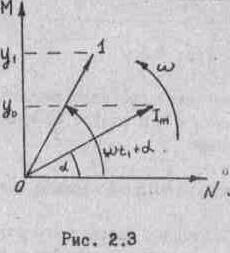 иберемо прямокутну систему координат /рис. 2.3/ і відкладемо з початку координат під кутом до горизонтальної осі вектор, довжина якого у вибраному масштабі дорівнює I_m .

Проекція цього вектора на вертикальну вісь

Примусимо обертатися вектор I_m із кутовою швидкістю проти годинникової стрілки /рис. 2.3/. В момент часу t₁ вектор буде займати положення і, а його проекція на вертикальну вісь

При безперервному обертанні проекція вектора I_m на верти­кальну вісь змінюється за сину­соїдним законом:

Вектор, що обертається, характеризує синусоїдну функцію в тому розумінні, що в будь-який момент часу амплітуда і фаза цієї функції відомі. Якщо в дві синусоїдні функції часу однієї частоти

,

,

то вони також можуть бути зображені векторами /рис. 2.4/.

Оскільки ці вектори обертаються з однаковою кутовою швидкістю , то в будь-який момент часу їх положення один відносно одного однакові. Між ними завжди зберігається кут

Я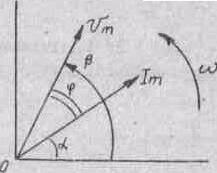 кщо синусоїдна функція повністю характеризується амплітудною і початковою фазою при відомій частоті, то початкове положення векторів повністю визначає синусоїдні функції і немає потреби зображати ці вектори

Рис 2.4

такими, що обертаються. Векторне зображення дає наочну картину взаємного розташування амплітуд синусоїдних функцій і дозволяв легко проводити простіші операції /додавання і віднімання/,

Сукупність векторів, які характеризують струми і напруги в електричному колі, називається векторною діаграмою.

Оскільки для одного будь-якого вектора початкова фаза може бути прийнята такою, що дорівнює нулю, то на векторній діаграмі можна не вказувати систему координат. Якщо величину векторів I_m, V_m зменшити в разів, то можна відкладати у вигляді векторів діюче значення.