4.3. Сети Петри

Сети Петри являются одним из самых старых методов описания параллельных процессов и предложены Карлом Петри в 1962 г. Они описывают не непосредственные связи между событиями в системе, а ситуации, при которых упомянутые события могут произойти.

Сети Петри могут быть представлены в аналитической и в графической форме. В первом случае становится возможной автоматизация процесса анализа, во втором – наглядное изображение параллельного процесса.

При графической интерпретации сети Петри представляют собой направленный граф с вершинами двух типов – позиций (обозначаются кружками) и переходов (обозначаются черточками). Направленные дуги могут связывать только вершины разных типов. Вершины-переходы соответствуют событиям, происходящим в системе, а позиции – условиям их возникновения. Совокупность этих трех элементов позволяет описать причинно-следственные связи в объекте в статике.

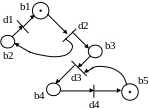
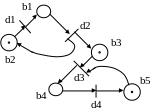
Кроме вершин и дуг сети Петри содержат еще один объект – фишки (метки) позиций. Переход считается активным, если в каждой его входной позиции находится хотя бы одна фишка. Расположение фишек называется разметкой сети. Пример изображения сети Петри при двух разметках приведен на рис. 4.9.

а)	б)
Рис. 4.9. Пример изображения сети Петри при двух разметках

В аналитической форме сеть Петри представляется в виде 5 компонент:

P = (B, D, I, O, M),

где	B	– конечное непустое множество позиций,
	D	– конечное непустое множество переходов,
	I	– входная функция, задающая для каждого перехода множество его входных позиций,
	O	– выходная функция, задающая для каждого перехода множество его входных позиций,
	M	– разметка сети.

Компоненты B и D являются перечнями вершин-позиций и вершин переходов, в которых обозначения вершин разделены запятыми. Для рис. 4.9 эти компоненты имеют вид: b1,b2,b3,b4,b5 и d1,d2,d3,d4.

Входные и выходные функции являются матрицами, в которых столбцы соответствуют переходам, а строки – позициям. В матрицах I и О элементы, находящиеся на пересечении столбцов, соответствующих переходам, и строк, соответствующих входным вершинам-позициям перехода, равны единице, в противном случае – нулю. Для рис. 4.9 эти матрицы показаны на рис. 4.10, а,б.

Разметка сети для рис. 4.9,а описывается последовательностью чисел (1,0,0,0,1), а для рис. 4.9,б – последовательностью (0,1,1,0,1). Единицы показывают наличие фишек в вершинах-позициях, а нули – их отсутствие. На рис. 4.9,а активен только переход d2, т.к. он имеет только одну входную вершину b1, в которой находится фишка. Переход d3 пассивен, т.к. он имеет две входных вершины и только в одной из них находится фишка. Осуществление события d2 сделало активным переход d1 и d3, т.к. фишка из вершины b1 перешла в вершины b2и b3. Смена разметки из М₀ в М₁ обозначается следующим образом:

Правило срабатывания перехода: Переход может сработать, только при наличии фишек во всех входных позициях

Правило изменения разметки: При срабатывании перехода фишки изымаются по одной из всех входных позиций и добавляются по одной в каждую выходную позицию.

d1 d2 d3 d4 b1 0 1 0 0 b2 1 0 0 0 b3 0 0 1 0 b4 0 0 0 1 b5 0 0 1 0 Fа)	d1 d2 d3 d4 b1 1 0 0 0 b2 0 1 0 0 b3 0 1 0 0 b4 0 0 1 0 b5 0 0 0 1 б)
Рис. 4.10. Входная (а) и выходная (б) функции для сети Петри (для рис. 4.9).

При анализе сети Петри исследования ведутся, как правило, в трех направлениях:

• исследование достижимости конкретной разметки М₁ при наличии некоторой стартовой разметки М₀ (т.е. исследование возможности достижения конкретного состояния системы при определенных начальных условиях);

• исследование живости переходов, т.е. возможности срабатывания переходов в данной сети при начальной разметке (т.е. выявление невозможных состояний системы);

• исследование безопасности сети – выявление невозможности появления в любой позиции более одной фишки (т.е. возможность работы сети в стационарном режиме).

Основным недостатком сетей Петри является невозможность моделиро­вать временные характеристики объектов.

Ниже приведены примеры исследования параллельных процессов с помощью сетей Петри. Первый пример описан в разделе 4.2 (рис. 4.4, 4.5). Для удобства изучения материала рисунки примера повторены ниже (рис. 4.11).

Рис. 4.11. Граф модели Холта	Рис. 4.13. Сеть Петри для первого примера
. . .
Parbegin
ПР1:
1: REQUEST(R1,3);
. . .
2: SAND_MASSAGE(ПР2, М1, ПЯ);
3: WAIT_ANSWER(М2, ПЯ);
. . .
4: RELEASE(R1,3);
ПР2:
. . .
5: WAIT_MASSAGE(ПР1, М1, ПЯ2);
6: REQUEST(R1,2);
. . .;
7: RELEASE(R1,2);
8: SAND_ANSWER(М1, ПЯ);
. . .
Parend Рис. 4.12. Код программы процессов

Позиция Р₁ соответствует началу процесса ПР1, а Р₉ – началу процесса ПР2. Позиция Р₂ соответствует выполнению оператора 1 и получению процессом 3-х единиц ресурса R, который изображает позиция Р₆. Прохождение перехода t₂ соответствует выполнению оператора 2, т.е. посылке сообщения процессу ПР2. Позиция Р3 соответствует ситуации "выполнен оператор 2". Процесс остановлен до получения сообщения от процесса ПР2. Если это сообщение придёт, то процесс продолжится, выполнится оператор 4 и процесс ПР1 освободит ресурс R (переход t₄). Однако процесс ПР2 ожидает сообщения от ПР1. Сообщение вызовет прохождение через переход t₅ в позицию Р₁₀. В ней процесс остановится, т.к. у ресурса R свободна только одна единица, а нужно две. Процесс ПР2 остановлен и не может послать сообщение процессу ПР1, а тот, в свою очередь, не получив сообщение, не может освободить ресурс R. Возник тупик.

Второй пример, иллюстрировавший возникновение тупика на ресурсах SR также рассматривался разделе 4.2 (рис. 4.6 и 4.7). Исследование возникновения тупика проиллюстрировано на рис. 4.14 – 4.15.

Рис. 4.14. Граф модели Холта	Р3 Р7 . . t1 t5 Р8 Р4 t2 . t6 Р5 Р1 Р9 t7 t3 Р6 Р2 Р10 . t4 t8 Рис. 4.16. Сеть Петри для первого примера
. . .
Parbegin
Parbegin
ПР1:
1: P(S2); . . .
2: P(S1); . . .
3: V(S1); . . .
4: V(S2); . . .
ПР2:
5: P(S1); . . .
6: P(S2); . . .
7: V(S1); . . .
8: V(S2); . . .
Parend Рис. 4.15. Код программы процессов

На рис. 4.16 номера переходов соответствуют номерам отмеченных операторов управления семафорами, позиции Р₁ и Р₂ – семафорам S₁ и S₂. Из него видно, при прохождении перехода t₁ процесс ПР1 захватывает ресурс Р₂, а процесс ПР2 при прохождении перехода t₅ захватывает ресурс Р₁. Дальнейшие попытки выполнить переходы t₂ и t₆ переводят процессы в состояние ожидания, поэтому t₃, t₄, t₇ и t₈ никогда не будут выполнены.

Сети с выполняющимися переходами называются живыми. С этой точки зрения сети, показанные на рис. 4.13 и 4.16 не являются живыми.

Графическое представление сетей Петри позволяет придать наглядность процессу исследования процессов на возникновение тупиков. Применение математического описания сети Петри позволяет автоматизировать процесс исследования. Можно считать также перспективной автоматизацию процесса исследования на основе математического описания сети Петри с визуализацией процесса исследования посредством графического представления сети.