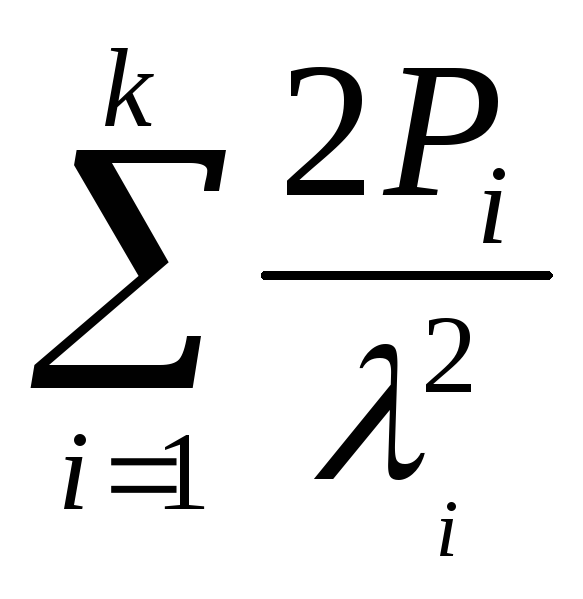1.3. Числовые характеристики случайных величин.

Числовые характеристики позволяют выражать в сжатой форме наиболее существенные особенности распределения случайной величины. В теории вероятности используется большое количество числовых характеристик, имеющих различное назначение и различные области применения. Из них наиболее часто используются начальные и центральные моменты. С помощью числовых характеристик существенно облегчается решение многих вероятностных задач, когда использование законов распределения приводит к громоздким выкладкам и не позволяет получить результаты в явном виде.

Д ля того, чтобы дать общее определение моментов одновременно для дискретных и непрерывных случайных величин, рассмотрим случайную величину X и предположим, что она описывается вероятностями P₁, P₂, ..., P_m ее возможных значений х₁, х₂,..., х_m, если Х - дискретная величина, и плотностью распределения f(x), если Х - непрерывная случайная величина.

Н

, если X – ДСВ;

, если X – НСВ.

ачальный момент n-го порядка, обозначаемый через M[Xⁿ] или Хⁿ, случайной величины Х определяется как:

(1.14)

M[Xⁿ]=Xⁿ =

- для ДСВ;

- для НСВ.

Первый начальный момент (n=1) случайной величины Х называется математическим ожиданием или средним значением случайной величины и, согласно (1.14), задается равенством:

(1.15)

M[X]=X=

Следует отметить, что начальный момент n-го порядка случайной величины - это математическое ожидание ее n-ой степени.

Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых, то есть

M[X₁+X₂+…+X_m]=M[X₁]+M[X₂]+…+M[X_m]

и здесь неважно, зависимы или независимы случайные величины X₁ , X₂ , ... , X_m. В то же время математическое ожидание произведения случайных величин равно произведению математических ожиданий, то есть

M[X₁X₂…X_m]=M[X₁]M[X₂]…M[X_m]

только в том случае, когда случайные величины независимы.

Рассмотрим теперь непрерывную случайную величину Y, которая является функцией другой случайной величины Х, то есть Y=g(X).

Тогда математическое ожидание случайной величины Y определяется через плотность распределения ее аргумента X равенством:

M[Y]=M[g(X)]= .

Э

, если X – ДСВ;

, если X – НСВ.

тот результат известен как основная теорема о математических ожиданиях.

Ц ентральный момент n-го порядка случайной величины Х определяетcя как:

M[(X-X)ⁿ]= (1.16)

Р азность Х-Х между случайной величиной и математическим ожиданием называется центрированной случайной величиной и характеризует отклонение случайной величины от ее среднего значения. Очевидно, что центральный момент n-го порядка случайной величины есть математическое ожидание n-ой степени соответствующей центрированной случайной величины. Легко показать, что для случайной величины центральный момент 1-го порядка или математическое ожидание центрированной случайной величины всегда равно нулю:

M [(X-X)]=M[X]-M[X]=X-X=0.

В торой центральный момент M[(X-X)²] называется дисперсией случайной величины и обозначается через D[X] или D_x . Для непосредственного вычисления дисперсии, согласно (1.16), служат формулы:

- для ДСВ;

- для НСВ.

D_x=D[X]= (1.17)

Дисперсия может быть определена через математическое ожидание и второй начальный момент:

D_x=M[(X-X)²]=M[X²-2XX+(X)²]=M[X²]-2XM[X]+(X)²=

=X²-2XX+(X)²=X²-(X)². (1.18)

Дисперсия суммы независимых случайных величин Х₁, Х₂, ..., Х_m равна сумме их дисперсий, то есть:

D[X₁+X₂+…+X_m]=D[X₁]+D[X₂]+…+D[X_m].

Предположим теперь, что количество случайных величин в сумме тоже случайно, то есть определим случайную величину

Y = ,

где N - случайная величина со средним значением N и дисперсией D_n , а Х₁, Х₂,..., Х_n - одинаково распределенные независимые случайные величины. В этом случае математическое ожидание и дисперсия случайной величины Y определяются равенствами:

Y =NX;

D _y=ND_x+(X)²D_n.

Дисперсия случайной величины характеризует рассеивание, то есть разброс случайной величины относительно ее математического ожидания, и имеет размерность квадрата случайной величины. Однако удобнее пользоваться характеристикой рассеивания, размерность которой совпадает с размерностью случайной величины. Такой характеристикой является среднее квадратическое отклонение, обозначаемое как [X] или _x и определяемое как квадратный корень из дисперсии:



(1.19)

[X]=_x=

Т аким образом, математическое ожидание X и дисперсия D_x (или среднее квадратическое отклонение _x) характеризуют наиболее важные особенности распределения: его положение и степень разбросанности.

В некоторых случаях в качестве безразмерной характеристики разброса значений случайной величины относительно математического ожидания используют коэффициент вариации, который определяется как отношение среднего квадратического отклонения к среднему значению:

(1.20)

_x= .

Используя выражения (1.18) - (1.20), можно получить соотношение, связывающее второй начальный момент случайной величины с коэффициентом вариации:

X

(1.21)

²=X²(1+ )

В таблице приведены основные числовые характеристики (математическое ожидание, второй начальный момент, дисперсия, среднее квадратическое отклонение, коэффициент вариации) для различных распределений, рассмотренных ранее в данном разделе.

Числовые характеристики распределений.

Распределение	M[X]		D[X]	[X]	x
Пуассона	a	a(a+1)	a
Геометрическое
Экспоненциальное	1/	2/2	1/2	1/	1
Эрланга	k/	k(k+1)/2	k/2	/	1/
Гиперэкспоненциальное порядка k			X2-X2
Равномерное