Расчёт констант равновесия (Ka, Кр, кn, Кс).

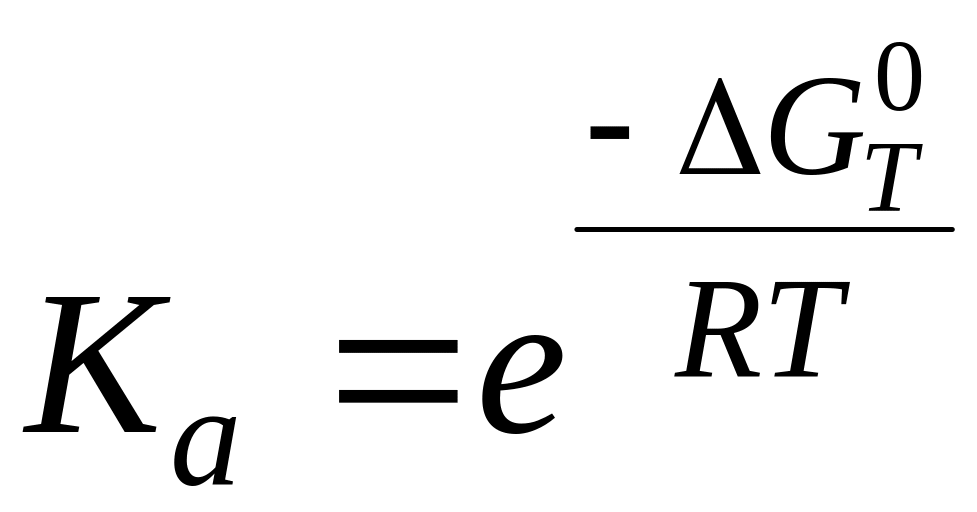, где а = γP, K_a = K_γK_p.

Если Р ≤ 1атм., γ → 1, K_γ ≈ 1, тогда K_a = K_p.

Если Р = 1атм., то K_p = K_N.

.

Пример расчёта равновесного состава:

K_a = K_γK_p, где K_γ – константа равновесия, выраженная через коэффициенты активности. Рассчитывается для газовых реакций по справочным данным, если Р >> 1 атм. Если давление в системе не велико K_γ → 1 и K_a = K_p.

1. Область невысоких давлений (Р ≤ 1 атм.)

C₂H₆ ↔ C₂H₄ + H₂ (реакционная смесь имеет стехиометрический состав). Обозначим через X конверсию исходных веществ в момент равновесия.

Компонент	Состав, моль
	исходные	равновесные
C2H6	1	1 – X
C2H4	−	X
H2	−	X

∑n_i = 1 – X + X + X = 1 + X

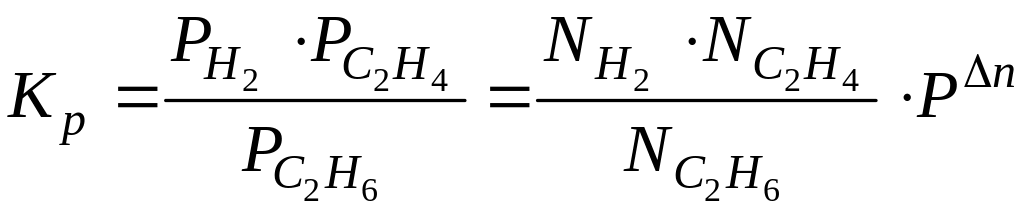, где ∆n = (1 + 1) – 1 = 1.

P_i = N_iP;

;

;

Зная численное значение константы, найдём X:

X = ;

X может быть равен нулю, то есть константа очень мала и реакция не идёт в прямом направлении. Если константа слишком велика (т. е. равновесие сдвинуто вправо), X в пределе будет равен максимальной величине стехиометрического коэффициента (при условии, что расчёт ведут по стехиометрическому составу).

2. Равновесный состав в объёмных процентах.

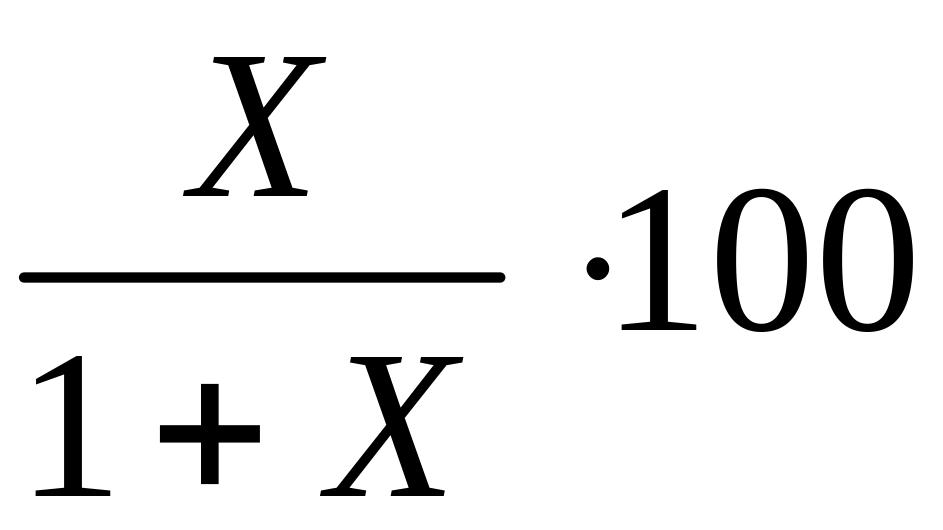%_i = N_i∙100%;

= = ;

= ∙100;

Пример заполнения таблиц и выражения констант для более сложных реакций (по стехиометрии):

3H₂ + N₂ ↔ 2NH₃;

Компонент	Состав, моль.
	исходные	равновесные
H2	3
N2	1
NH3	−	X

3 моль H₂  2 моль NH₃;

? моль H₂  X моль NH₃;

3X = 2∙?;

? = ;

1 моль N₂ → 2 моль NH₃;

? моль N₂ → X моль NH₃;

2∙? = X;

? = ;

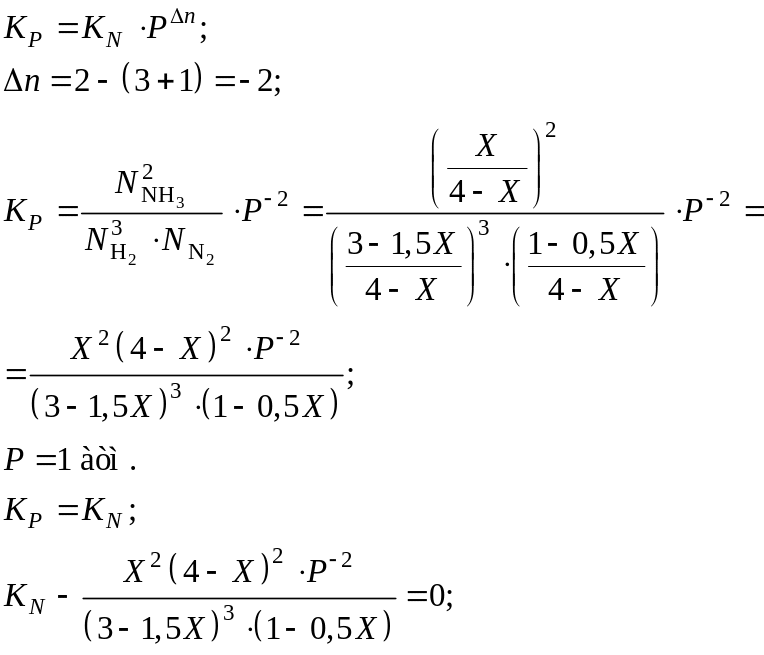
(∆ – отклонение).

Выражение константы К_с для данной реакции.

Состав не стехиометрический, а произвольный.

Например, вышеуказанная реакция имеет 1 моль H₂, 2 моля N₂, 0,5 моля NH₃.

Сначала таблица заполняется по стехиометрии, потом – произвольно.

∆n – считается по стехиометрии.

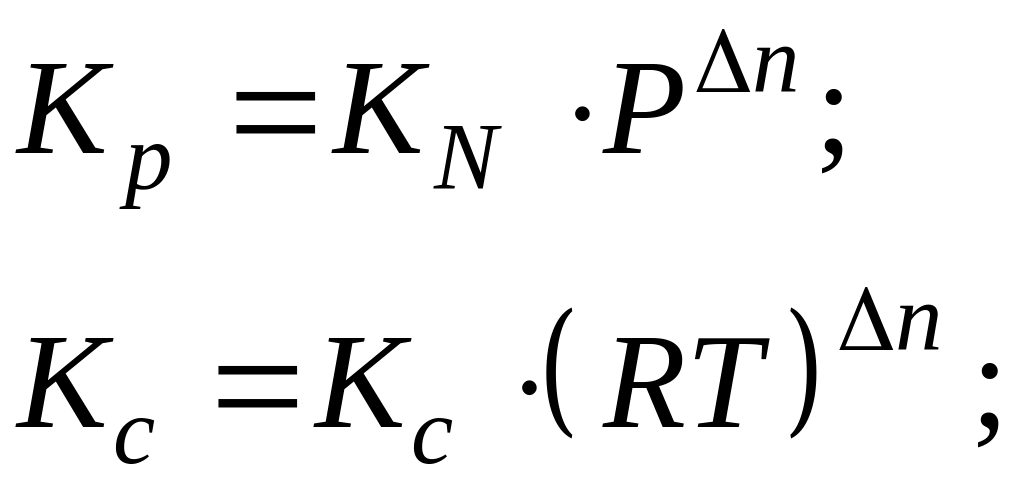
Но при расчёте суммы молей учитывается состав, который задан.

Выражение константы равновесия для гетерогенных реакций.

Активности (парциальные давления) твёрдых фаз, принимаются равными единице, в таблицу их не включают и при расчёте константы не учитывают.

Например:

Компонент	Состав, моль.
	исходные	равновесные
CО	1	1 – X
CО2	−	X

Открытые системы, химический потенциал, условия равновесия.

В этих системах наряду с энергообменом происходит массообмен со средой. Для учёта изменения или перераспределения числа молей компонента в ходе массообмена вводится новая функция – химический потенциал. Для неизолированных систем энергия Гиббса была функцией двух переменных G = f(P, T) и выражалась dG = VdP – SdT; в открытых системах помимо P и T энергия Гиббса будет ещё и функцией компонентов системы , где – моли компонентов.

С учётом этого выражаем полный дифференциал:

где n_i – постоянное число всех молей компонентов системы; n_f – постоянное число всех молей компонентов системы, кроме одного изменения, которое рассматривается.

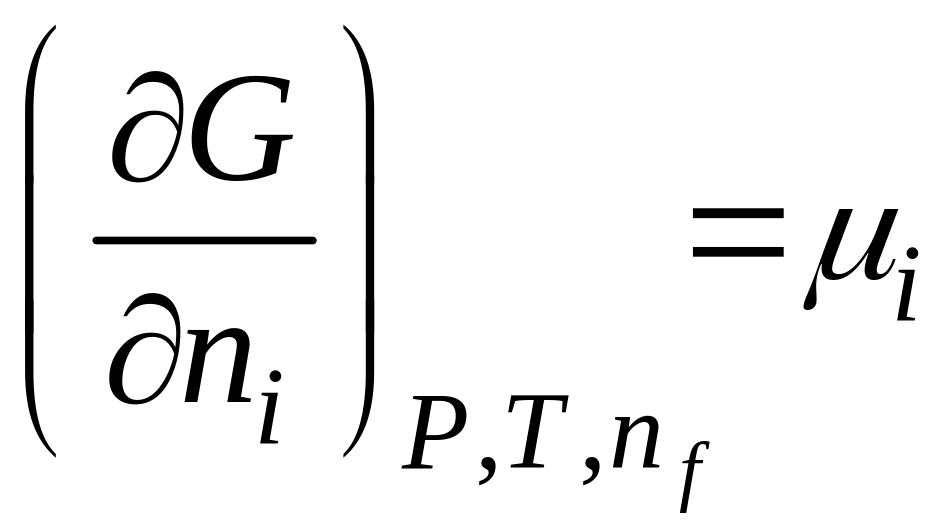– химический потенциал.

Примечание: потенциал  выражают аналогично через F, H или U, поэтому химическим потенциалом компонента называется частная производная от любого другого потенциала по числу молей этого компонента при постоянстве соответствующих параметров состояния.

При P и T = const, dP, dT = 0;

Для состояния равновесия dG = 0, следовательно – условие равновесия для систем с массообменом.

19