Влияние внешних условий на равновесие.

1. Влияние давления:

Соотношение между константами К_р и К_N выражается в виде:

;

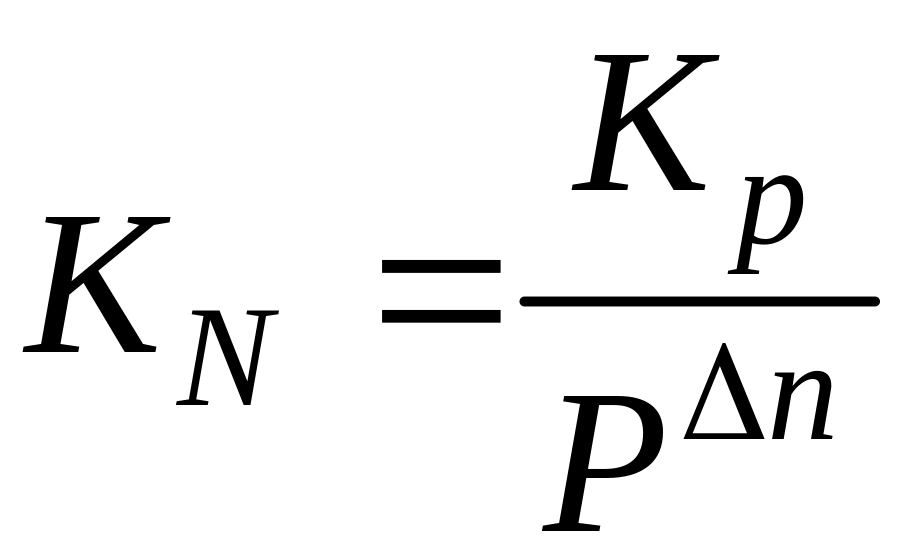Из выражения следует, что константа К_N будет зависеть от общего давления в системе. Характер этого влияния определяется членом ∆n. Если реакция идет с увеличением числа молей, то есть ∆n > 0, рост давления смещает равновесие справа налево; если с уменьшением числа молей, то есть ∆n < 0, с ростом давления равновесие смещается слева направо; если без изменения числа молей (∆n = 0), изменение давления на сдвиг равновесия не влияет. В последнем случае К_р = К_N.

Примечание: в ряде случаев реакционная смесь может быть разбавлена газом, инертным по отношению к участникам реакции. Влияние ввода этого газа на равновесие аналогично уменьшению общего давления в системе.

2. Влияние температуры:

Уравнения изобары и изохоры.

Для вывода используется уравнение Гиббса-Гельмгольца:

Вывод уравнения изобары:

В уравнение Гиббса подставляется уравнение изотермы для состояния равновесия ( P ≤ 1атм ).

∆G_T⁰ = –RTlnК_р;

–RTlnК_р = ∆H – RTlnК_р – ;

– уравнение изобары в дифференциальном виде;

Интегрирование при H = const:

;

По этому уравнению, зная две константы при двух температурах, можно определить ∆H или, зная тепловой эффект и константу при какой-либо температуре, легко можно определить константу при любой другой температуре.

;

Графический анализ уравнения.

Из графика следует: для экзотермической реакции рост температуры приводит к сдвигу равновесия справа налево; для эндотермической – слева направо. Если протекание реакции не сопровождается поглощением или выделением тепла (∆H = 0), изменение температуры на равновесие не влияет.

Примечание: для качественного определения сдвига равновесия при изменении тех или иных внешних факторов используют принцип Ле-Шателье: Если на систему, находящуюся в равновесии, оказывают внешнее воздействие, в системе идет сдвиг равновесия, ослабляющий это воздействие.

Третье начало термодинамики.

Включает тепловую теорему Нернста и постулат Планка. Последний имеет прикладное значение при расчёте химического равновесия.

Постулат Планка:

В области абсолютного нуля температуры энтропия правильно сформированного кристалла равна нулю (T = 0 K, S = 0). Это подтверждается и формулой Больцмана, так как при 0 K термодинамическая вероятность системы W равна 1, то S = 0. Постулат Планка не является абсолютно строгим, так как некоторые составляющие энтропии, обусловленные спиновым и изотропным эффектами, не будут равны нулю, но при протекании химических реакций ими пренебрегают. Практическое значение постулата Планка заключается в возможности теоретического расчета абсолютного значения энтропии.

Например:

;

;

Обычно справочные значения абсолютных энтропий рассчитывают в интервале 0 – 298 K. ( – справочное значение).

Теоретический расчёт химического равновесия

Теоретический расчёт химического равновесия проводят с использованием абсолютных значений энтропии.

1. Расчёт – стандартного изменения энергии Гиббса при стандартной температуре (a = 1, T = 298 K).

a) = – 298∙ ;

= ∑n_кон( )_кон – ∑n _исх( )_исх;

б) = ∑n_кон( )_кон – ∑n_исх( )_исх;

– изменение энергии Гиббса при образовании какого-либо соединения из простых веществ. Для простых веществ она равна нулю.

Примечание: при расчёте пользуются обоими методами.

2. Расчёт (a = 1, T = любая).

a) = ;

= + – уравнение Кирхгофа.

;

;

Для реакции в целом: ;

;

;

– значения двойных интегралов, рассчитанных авторами метода при соответствующих коэффициентах теплоёмкости.

б) ;

Заменим константы К_р на K_a, вместо ∆H подставим интегральную форму уравнения Кирхгофа, когда ∆C_p = f(T).

;

Интегрируем и домножаем обе части на –RT, учитывая

–RTlnK_a = ∆G⁰_T

, где Y – константа интегрирования в этом выражении. Для её определения вместо ∆G⁰_T подставляют ∆G⁰₂₉₈, а вместо T – 298 К. Далее расчёт проводят при температуре, которая задана.

Примечание: в расчётном задании ∆G⁰_T считают обоими методами.