Лабораторная работа №2

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Лабораторная работа №2

Многомерная безусловная оптимизация

Выполнил

студент группы АСОИ-331

Гатфанов Р.

Проверил:

Хасанов А.Ю.

Уфа - 2007

Цель работы: знакомство с методами многомерной безусловной оптимизации первого и нулевого порядка и их освоение, сравнение эффективности применения этих методов конкретных целевых функций.

Задание:

Целевая функция f(x)=f(x⁽¹⁾, x⁽²⁾) зависит от двух аргументов. Функция f(x) следующего вида:

f(x)=a*x­₁+b*x₂+

№	Целевая функция				Начальное приближение	Точность решения
	a	b	c	d
6	11	-0.4	1	0,21	(-1;0)	0,0001

Для решения задачи использовать методы:

а) градиентный метод с постоянным шагом;

к) метод конфигураций.

Блок–схема градиентного метода с постоянным шагом:

начало

x₀, ε, α,

f(x₁,x₂)=11x₁-0.4x₂+

k=0

f ^/(x_k)

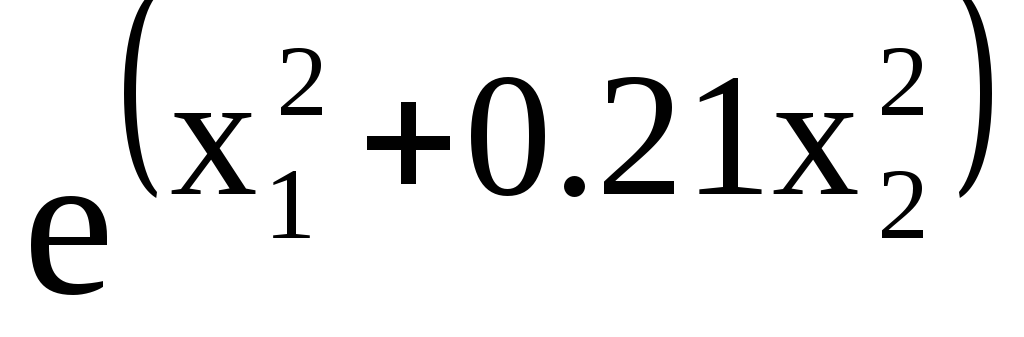
x_k+1 = x_k – α f ^/(x_k)

f ^/(x_k+1)

|| f ^/(x_k+1)|| ε

k=k+1

да

нет

конец

Блок–схема метода конфигураций:

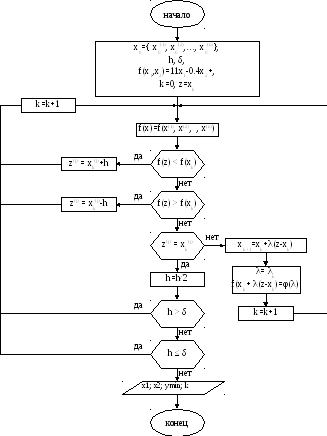
Текст программы:

Гр.метод с пост шагом:

#include <stdio.h>

#include <math.h>

#include <stdlib.h>

#include <conio.h>

#include <iostream.h>

double a = 11,

b = -0.4,

c = 1,

d = 0.21;

double x1[1000], x2[1000];

double E = 0.0001;

double ak = 0.05;

int s;

double func(double x1,double x2)

{s++;return a*x1+b*x2+exp(c*x1*x1+d*x2*x2);}

double funcdx1(double x1,double x2) // производная по dx1

{s++;return a+2*c*x1*exp(c*x1*x1+d*x2*x2);}

double funcdx2(double x1,double x2) // производная по dx2

{s++;return b+2*d*x2*exp(c*x1*x1+d*x2*x2);}

void gr()

{

cout<<" GRADIENTNYII METOD S POSTOYANNYIM SHAGOM:\n";

double xnt1=-1, xnt2=0, xpr1=0, xpr2=0, funpro=0;

int i=0;

do

{ i++;

xnt1=xpr1-ak*funcdx1(xpr1, xpr2);

xnt2=xpr2-ak*funcdx2(xpr1, xpr2);

funpro=funcdx1(xnt1, xnt2)+funcdx2(xnt1, xnt2);

xpr1=xnt1;

xpr2=xnt2;

cout<<"і "<<i<<"\tі "<<xnt1<<"\tі "<<xnt2<<"\tі "<<func(xnt1, xnt2)<<"\tі\n";

}while(fabs(funpro)>E);

cout<<"MINIMUM PRI \tx1=\t\t"<<xnt1<<"\n\t\tx2=\t\t"<<xnt2<<"\n\t\tf(x1,x2)=\t"<<func(xnt1, xnt2)<<"\n\t\tk = "<<i<<"\n\t\ts =\t"<<s<<"\n";

}

void main()

{

gr();

}

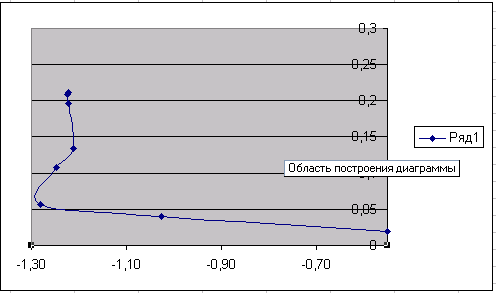
Метод конфигураций:

#include<iostream.h>

#include<math.h>

#include<stdio.h>

#include<conio.h>

double x1[1000], x2[1000], y[4];

double e=0.0001;

double a=11, b=-0.4, c=1, d=0.21;

double z1, z2;

int N;

int k;

double A,B;

double func(double x1,double x2)

{

N++;

return a*x1+b*x2+exp(c*pow(x1,2)+d*pow(x2,2));

}

void konf()

{

double x1min, x2min, ymin;

N=0;

x1[0]=-1

x2[0]=0;

double l=1,h=1;

int s=1; //условие выхода из цикла

k=0;

y[0]=func(x1[0],x2[0]);

do

{

s=1;

y[1]=func(x1[k]+h,x2[k]);

if(y[0]>y[1])

x1[k+1]=x1[k]+h;

else

{

y[1]=func(x1[k]-h,x2[k]);

if(y[0]>y[1])

x1[k+1]=x1[k]-h;

else

{

y[1]=y[0];

x1[k+1]=x1[k];

}

}

y[2]=func(x1[k+1],x2[k]+h);

if(y[1]>y[2])

x2[k+1]=x2[k]+h;

else

{

y[2]=func(x1[k+1],x2[k]-h);

if(y[1]>y[2])

x2[k+1]=x2[k]-h;

else

{

y[2]=y[1];

x2[k+1]=x2[k];

}

}

printf("x1[%d]=%f, x2[%d]=%f\n",k,x1[k],k,x2[k]);

printf("x1[%d]=%f, x2[%d]=%f\n",k+1,x1[k+1],k+1,x2[k+1]);

getch();

if((x1[k+1]==x1[k])&&(x2[k+1]==x2[k]))

{

if(h>e)

{

s=0;

h=h/2;

}

}

else

{

s=0;

do

{

l=l/2;

x1[k+2]=x1[k+1]+l*(x1[k+1]-x1[k]);

x2[k+2]=x2[k+1]+l*(x2[k+1]-x2[k]);

y[3]=func(x1[k+2],x2[k+2]);

}

while(y[2]<y[3]);

y[0]=y[3];

k=k+2;

}

}

while(s==0);

x1min=x1[k];

x2min=x2[k];

ymin=y[0];

cout<<endl;

cout<<"X1 = "<<x1min<<endl;

cout<<"X2 = "<<x2min<<endl;

cout<<"Y = "<<ymin<<endl;

cout<<"N = "<<N<<endl;

cout<<"k = "<<k<<endl;

getch();

}

void main()

{

konf();

}

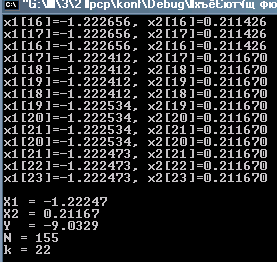
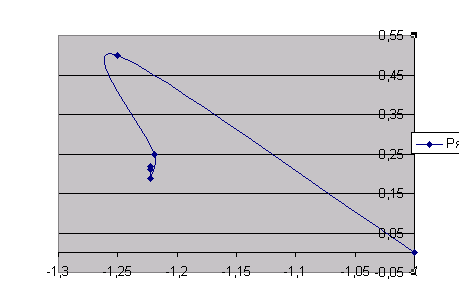
Сравнение результатов:

x1	x2	f(x1, x2)	Кол-во эксп-ов
Градиентный метод с постоянным шагом
-1,22248	0.211636	-9,0329	420
Метод конфигураций
-1,22247	0.21167	-9,0329	155

Вывод: как видно из результатов таблицы заданная точность достигается быстрее в методе конфигураций.