7. Рцкп (ротатабельный центральный композиционный план).

РЦКП обеспечивает незначимую величину ошибки в точках, равноотстоящих от центра проведения экспериментов, поэтому они широко применяются в динамических методах поиска экстремальных значений. Расстояние звёздной точки от центра осей координат и количество проводимых экспериментов в центральной точке вычисляются по формулам:

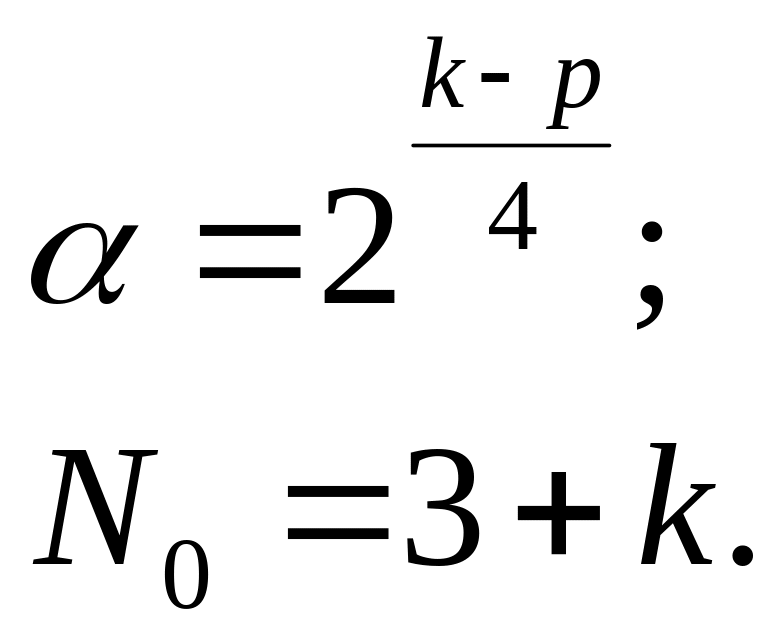Составим матрицу планирования РЦКП для двух факторов:

Композиционные планы ОЦКП и РЦКП имеют существенный недостаток, который начинает сказываться с увеличением количества факторов в проводимых экспериментах, чем больше факторов, тем больше расстояние звёздных точек от центра осей координат, которое всё больше и больше удаляется от заданных границ диапазонов изменения факторов, что является нежелательным.

7. Д – оптимальные планы.

В D – оптимальных планах значения факторов не выходят за установленные границы диапазонов их изменения. Кроме того они обладают ещё одним существенным достоинством, обеспечивая минимальную ошибку во всём принятом диапазоне изменения факторов. На практике наиболее часто применяются планы Коно и планы Кифера.

Планы Коно. Для многофакторных экспериментов в геометрической интерпретации диапазон изменения факторов представляется многомерным кубом, который далее будем называть просто куб. Для двух факторов этот куб вырождается в квадрат. Эксперименты по плану Коно проводятся в вершинах куба, серединах рёбер и центре куба. Характерной особенностью D – оптимальных планов является разница в количестве проводимых экспериментов для точек плана различного вида. Удельные веса видов точек для двухфакторных экспериментов в планах Коно приняты следующие. 1. Вершины куба - =0.148. 2. Середины ребер - =0.078. 3. Центр куба - =0.096. Расположение точек стратегического плана на квадрате и кубе представлено на рис.

Геометрическая интерпретация двухфакторного плана на квадрате и трёхфакторного – на кубе

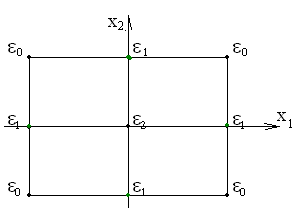
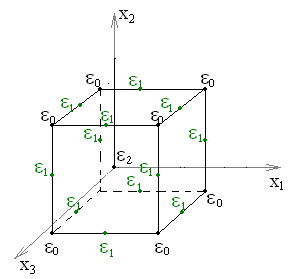
Количество точек для двухфакторного эксперимента (к=2) и трёхфакторного эксперимента (к=3)

к=2	к=3
=4 =4 =1	=8 =12 =1
9	21

Планы Кифера

Эксперименты по плану Кифера проводятся в вершинах куба, серединах рёбер и центрах граней. Для двухфакторных экспериментов по плану Кифера приняты следующие удельные веса. 1. Вершины куба - =0.1458. 2. Середины рёбер - =0.08015. 3. Центры граней - =0.0962.

Расположение точек плана для двухфакторных экспериментов представлено на рис.15.4; для трёхфакторных на рис.

Геометрическая интерпретация двухфакторного эксперимента Геометрическая интерпретация трёхфакторного

по плану Кифера на квадрате эксперимента по плану Кифера

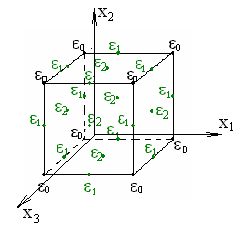
Количество точек в D – оптимальных планах приведено в таблице

к=2	к=3
=4 =4 =1	=8 =12 =6
9	26

В таблице 15.6 приведём план Коно для двухфакторного эксперимента; в таблице 15.7 – план Кифера, которые позволяют построить математическую зависимость вида:

.

Таблица 15.6

I	X0	X1	X2	X1X2	X21	X22	E1
1	1	-1	1	-1	1	1	0,148
2	1	0	1	0	0	1	0,078
3	1	1	1	1	1	1	0,148
4	1	-1	0	0	1	0	0,078
5	1	0	0	0	0	0	0,096
6	1	1	0	1	1	0	0,078
7	1	-1	-1	1	1	1	0,148
8	1	0	-1	-1	0	1	0,078
9	1	1	-1	-1	1	1	0,148

Таблица 15.7

I	X0	X1	X2	X1X2	X21	X22	E1
1	1	-1	1	-1	1	1	0,14580
2	1	0	1	0	0	1	0,08015
3	1	1	1	1	1	1	0,14580
4	1	-1	0	0	1	0	0,08015
5	1	0	0	0	0	0	0,09620
6	1	1	0	1	1	0	0,08015
7	1	-1	-1	1	1	1	0,14580
8	1	0	-1	-1	0	1	0,08015
9	1	1	-1	-1	1	1	0,14580

Отметим что для того, чтобы не потерять корректность D – оптимальных планов, чтобы количество реализаций в каждом варианте было целым числом, общее количество проводимых экспериментов для планов Коно требуется брать точно кратным 1000 а для планов Кифера – кратным 10000.