II этап моделирования. Формализация. Решение задачи. Выбор метода моделирования (подробно).
На данном этапе решаются следующие задачи:
Задача 1. Производится переход от функциональных зависимостей результативных показателей эффективности от влияющих на них факторов (1.1) к математическим зависимостям.
Задача 2. Количественные характеристики функционирования элементов ОМ, заданные на предыдущем этапе последовательностями случайных чисел, представляются стандартными статистическими законами.
Задача 3. Выбирается метод исследования.
1. При переходе от функциональных зависимостей к математическим нам известен закон, то есть вид математической зависимости результативных показателей эффективности от факторов и тогда задача сводится только к вычислению коэффициентов этой известной математической зависимости, но чаще всего вид математической зависимости не известен. В этом случае рекомендуется использовать для её представления степенные полиномы. При увеличении степени полинома можно через экспериментальные точки провести математическую зависимость с любой заданной достоверностью. На рис. показано представление экспериментальной зависимости, заданной координатами пяти точек, линейным полиномом и полиномом четвёртой степени. В последнем случае линия зависимости y=f(x) проходит точно через все экспериментальные точки. Линейное представление y=f(x) характеризуется некоторой ошибкой.
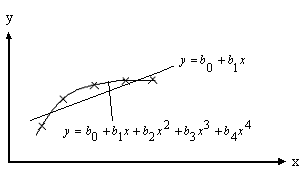Графическое
представление экспериментальных данных
степенными полиномами
Для однофакторной зависимости используется полином к-ой степени:
Для
двух факторов можно использовать полином
второй степени:
.
на данном этапе мы выбираем только вид аппроксимирующей зависимости – степенной полином. А степень полинома определяется по величине стандартной ошибки представления экспериментальных данных математической зависимостью.
3.2. Аппроксимация экспериментальных распределений случайных чисел стандартными статистическими законами.
На практике для аппроксимации наиболее часто применяется метод моментов. Суть метода моментов заключается в приравнивании оценок моментов, вычисленных по экспериментальным данным, соответствующим им моментам, вычисленным по функции плотности или моментной производящей функции (МПФ). Качество представления рекомендуется оценивать по критериям согласия.
Выбор метода моделирования.Основополагающим моментом при выборе метода моделирования являются результаты аппроксимации экспериментальных распределений случайных чисел, описывающих функционирование элементов системы. Естественно, что наиболее целесообразно использовать аналитические модели, не имеющие методической ошибки. Их можно считать законами функционирования элементов моделируемых систем. Недостаток аналитических моделей – сложность их составления. Особенно в случаях, когда законы функционирования элементов системы представляются составными экспоненциальными законами. Кроме того, часто в моделях требуется учитывать различные логические условия, которые невозможно выразить в аналитическом виде.Имитационное моделирование имеет более общий характер по сравнению с аналитическим и фактически оно позволяет проводить моделирование любых систем с любыми законами функционирования их элементов. Два существенных недостатка имитационного моделирования:
1.Наличие методической ошибки.
2.Точечный (табличный) характер представления результатов моделирования.
Ущерб от первого недостатка можно снизить проведением планирования экспериментов, цель которого получить результаты с заданной достоверностью при наименьших затратах. Ущерб от второго недостатка можно снизить с помощью обработки результатов моделирования с применением регрессионного анализа, позволяющего получить математические зависимости результативных показателей эффективности функционирования ОМ от влияющих на них факторов и таким образом приблизиться к результатам аналитического моделирования.
Большой класс моделей можно создавать и без описанного выше математического моделирования. Часто для этого достаточно собранных на натурном объекте статистических данных, отражающих работу исследуемого объекта моделирования за значительный промежуток времени в самых различных режимах функционирования.