10. План оцкп (ортогональный центральный композиционный план).

ОЦКП сохраняет свойство симметричности плана за счёт того, что на каждый фактор вводят по две симметричные звёздные точки. ОЦКП сравнительно несложно построить. ОЦКП в значительной мере упрощает вычисления, что особенно существенно для «ручных» вычислений. Свойство нормированности

в ОЦКП сохранить не удаётся, но это и не так важно. Для обеспечения ортогональности столбцов матрицы планирования вводят некоторые сравнительно несложные преобразования. Расстояние звёздной точки от середины осей координат вычисляется по формуле:

Вычисляется вспомогательный коэффициент:

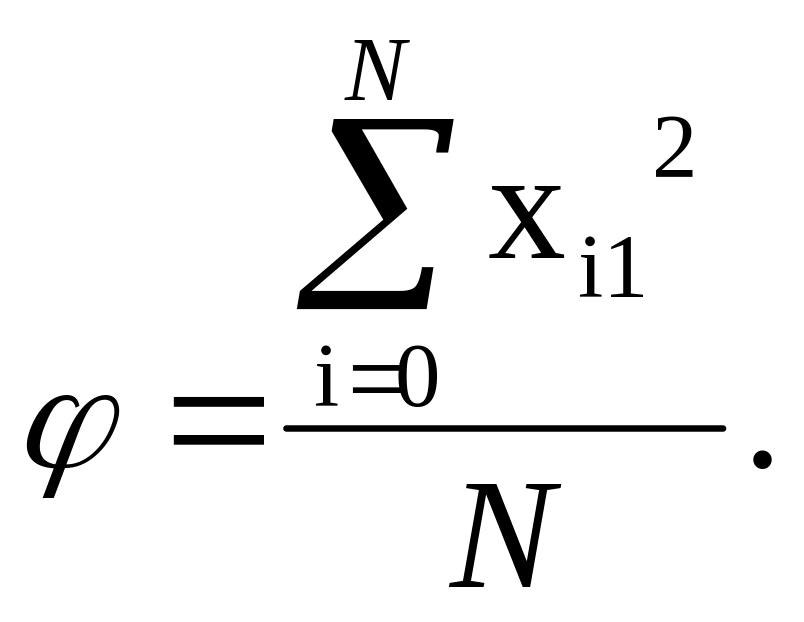
Вычисляются новые значения элементов столбцов квадратов факторов:

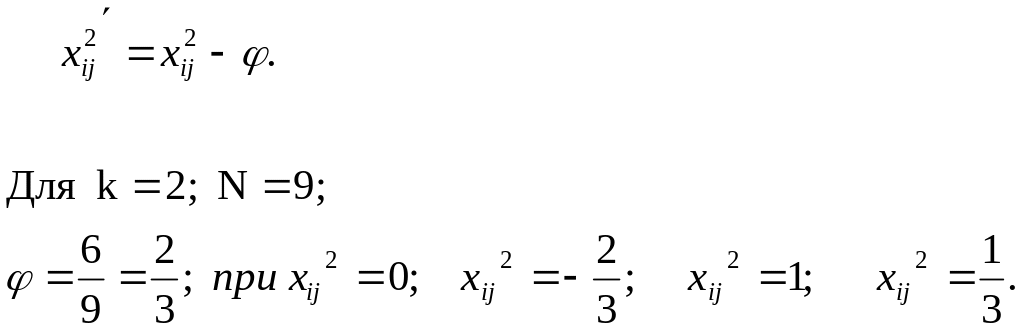
Матрица планирования для двух факторов по ОЦКП представлена в виде таблицы

	x0	X1	X2	x12	x12	x22
ЦТ	1	0	0	0	-2/3	-2/3
План ПФЭ	1 1 1 1	-1 1 -1 1	-1 -1 1 1	1 -1 -1 1	1/3 1/3 1/3 1/3	1/3 1/3 1/3 1/3
Звездные точки	1 1 1 1	-1 1 0 0	0 0 -1 1	0 0 0 0	1/3 1/3 -2/3 -2/3	-2/3 -2/3 1/3 1/3

11. Регрессионный анализ с примером для линейной зависимости y=b0+b1x.

Регрессионный анализ основан на методе наименьших квадратов, который требует, чтобы сумма квадратов отклонений экспериментальных значений от вычисленных по аппроксимирующей зависимости была минимальной:

В лучшем случае при обработке результатов экспериментов нам известен вид математической зависимости между переменными и тогда следует вычислить только неизвестные коэффициенты. Чаще всего вид математической зависимости неизвестен. В этом случае рекомендуется использовать степенные полиномы, которые при повышении степени полинома позволяют получать аппроксимирующие зависимости с любой заданной точностью.

Приведём запись уравнения в матричном виде и проведём его преобразование для получения формулы для вычисления коэффициентов полинома.

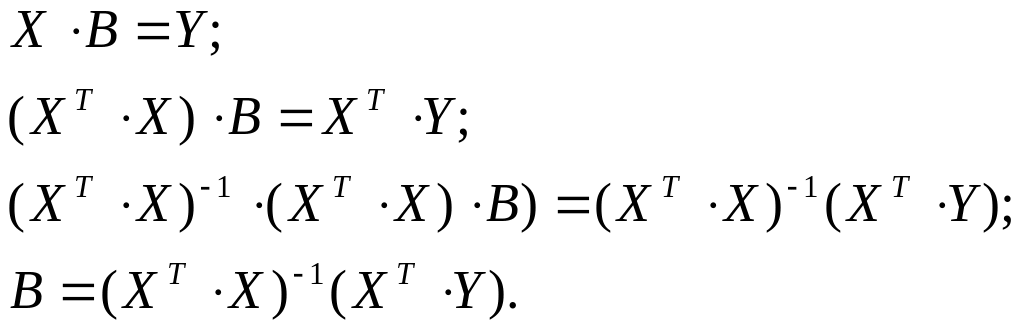
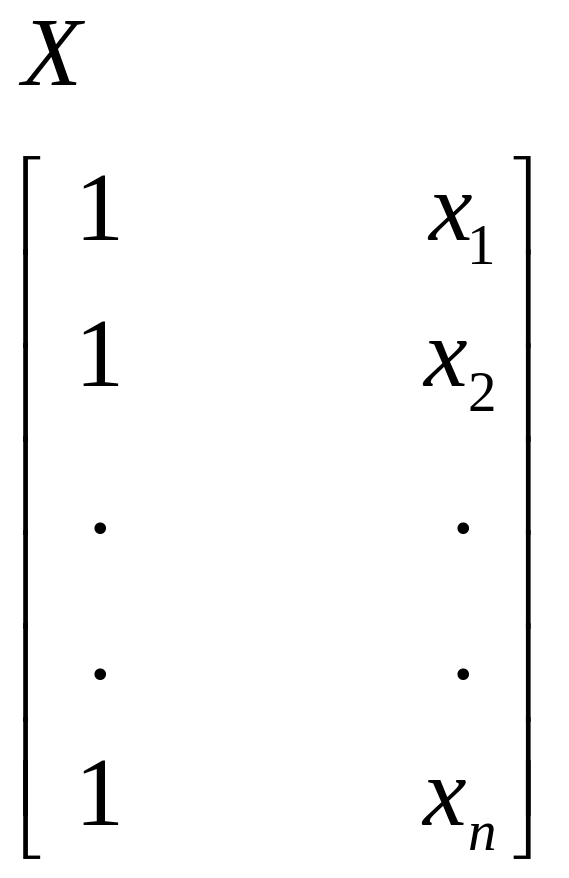
Рассмотрим самый простой пример однофакторной зависимости и проведём аппроксимацию этой зависимости линейной функцией: Пусть проведено экспериментов, по результатам которых получены значений и значений . Чтобы для вычисления коэффициентов и использовать один и тот же алгоритм введём в формулу фиктивную переменную , всегда равную единице. Составим матрицы X и Y:

Проведём несложные матричные преобразования и получим формулы для вычисления коэффициентов полинома

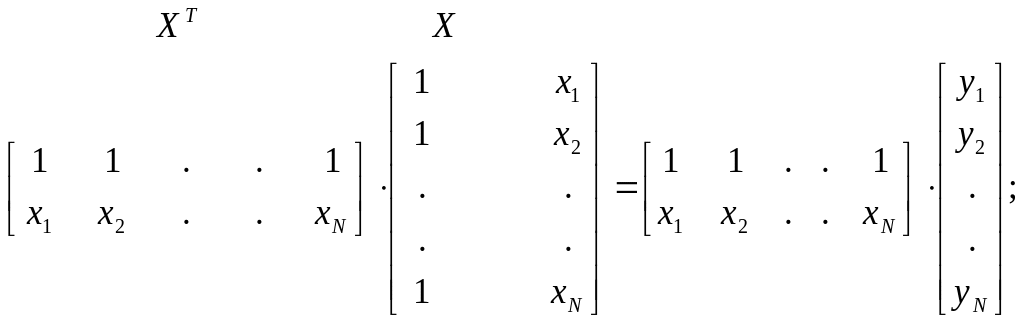
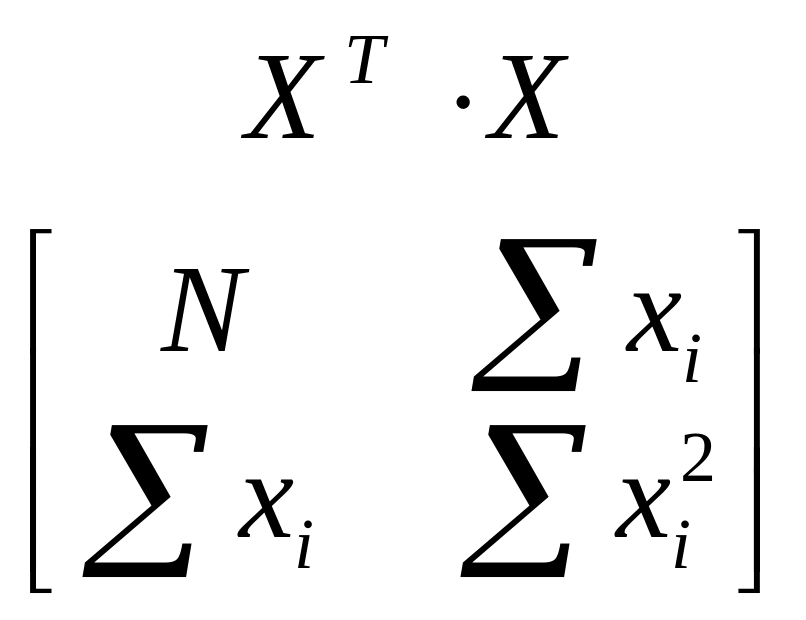
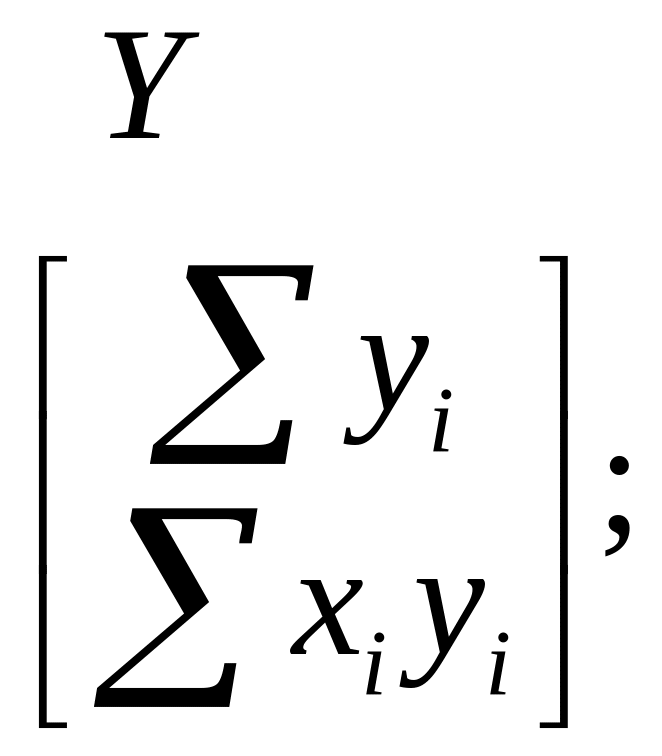
Требуется провести обращение матрицы , т. е. получить матрицу Умножение обратной и «своей» прямой матрицы даёт в произведении единичную матрицу, в которой элементы главной диагонали равны единице, а остальные элементы равны нулю.

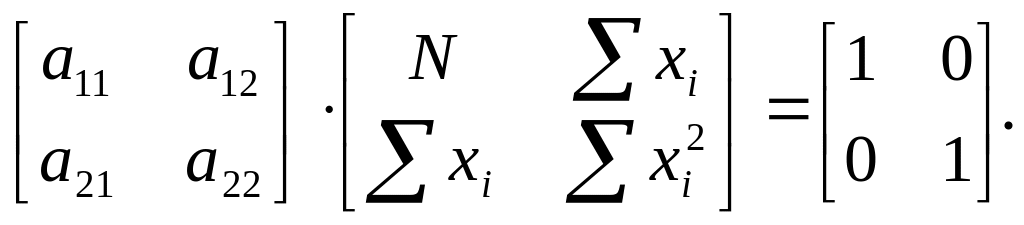
После несложных преобразований систем уравнений получим расчётные формулы для вычисления коэффициентов элементов матрицы А.

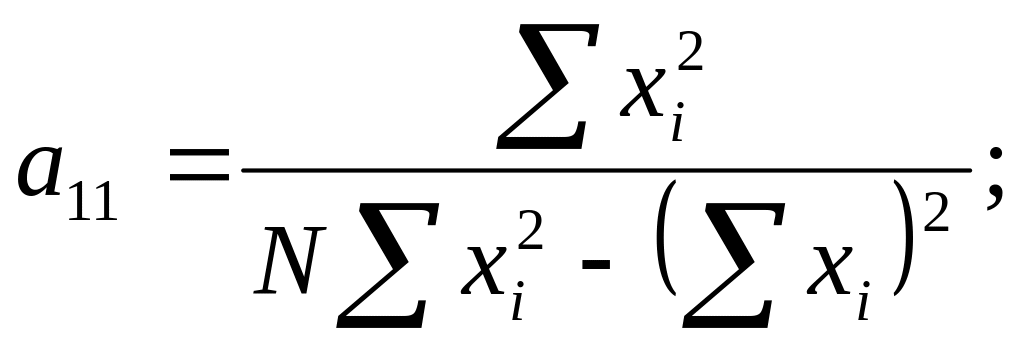
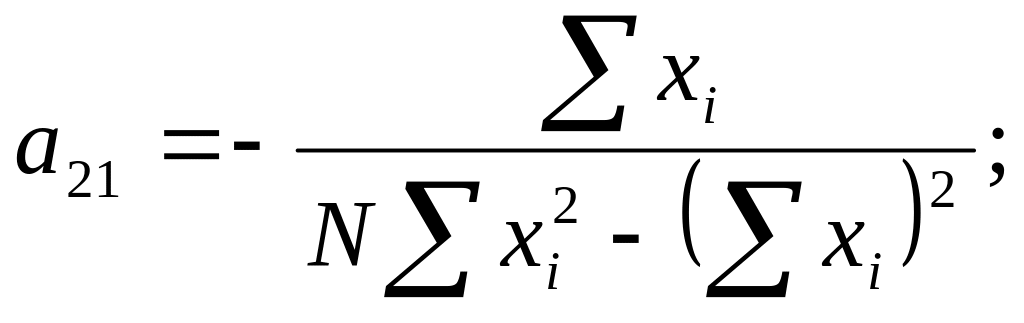
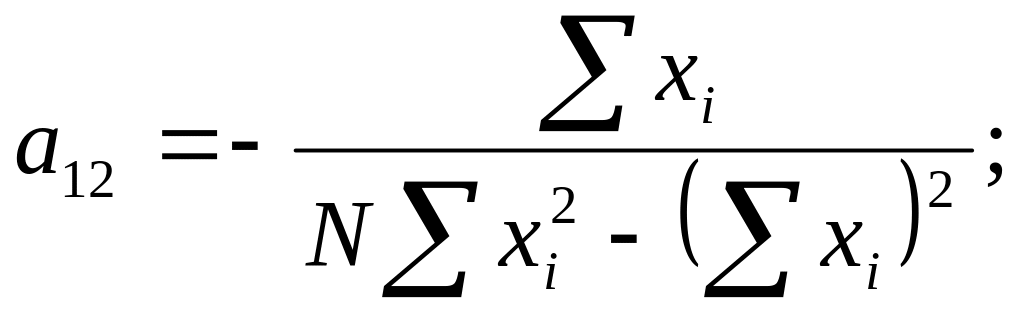
Проведём проверку результатов проведённых преобразований, обозначив знаменатель у всех коэффициентов :

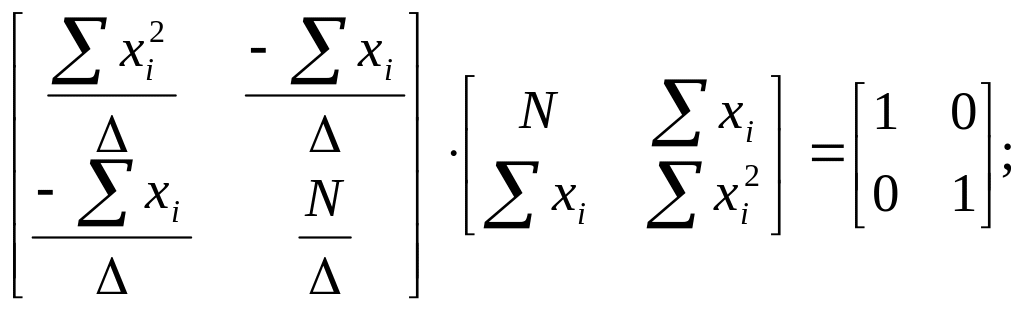
Таким образом все преобразования проведены корректно. Всё решено правильно. Запишем окончательный результат:

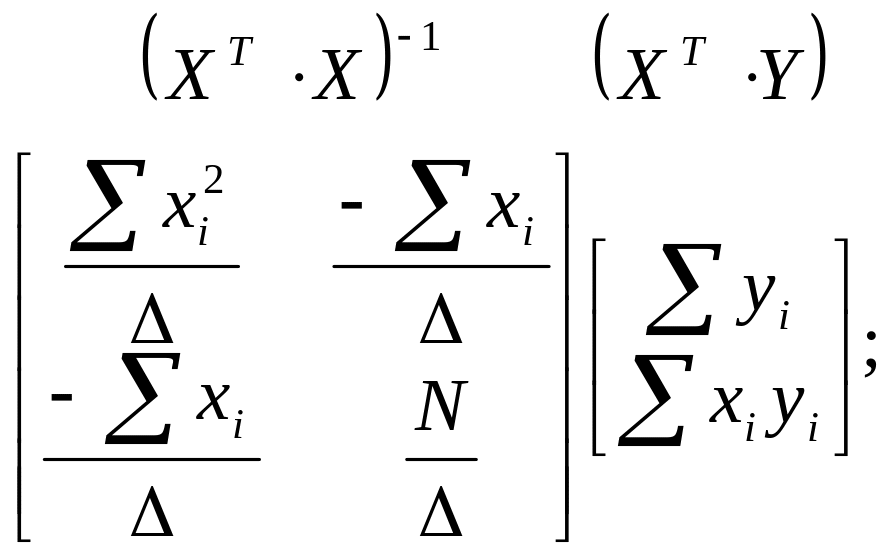
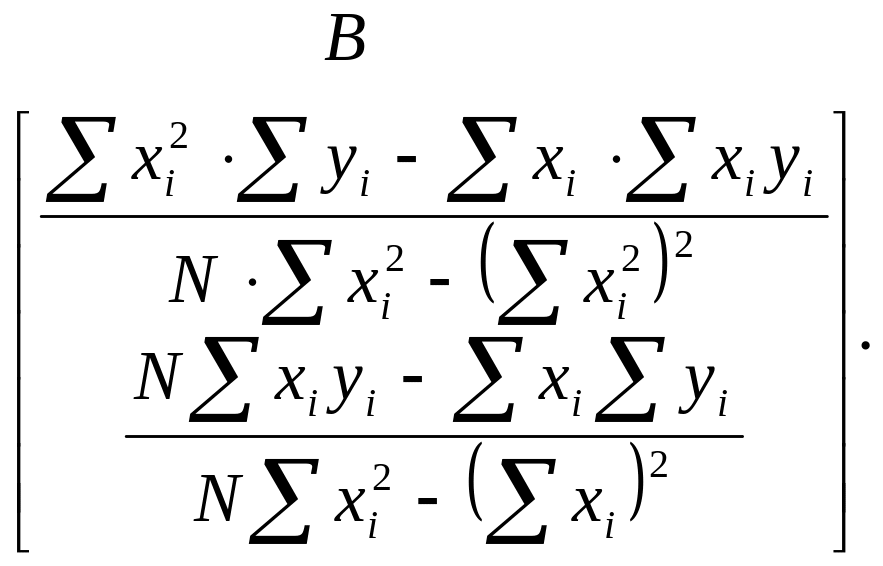
Если линейное уравнение регрессии не удовлетворяет поставленным требованиям по каким-либо параметрам, то рекомендуется перейти к нелинейной регрессии;

Основной показатель качества представления экспериментальных данных уравнениями регрессии – величина стандартной ошибки, вычисляемая по формуле: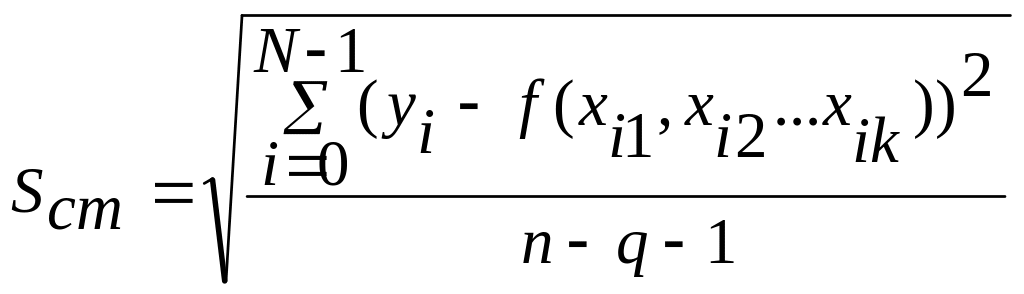 .