2. Метод моментов. Специальный эрланговский закон.

Специальное эрланговское распределение состоит из к последовательно соединенных фаз, в каждой из которых распределение случайных величин подчиняется экспоненциальному закону с одинаковой интенсивностью к. Структурная схема специального эрланговского закона распределения представлена на рис.

 к к к

….

Структурная схема специального эрланговского закона распределения случайных чисел

Ценность такого представления в том, что закон определяется всего двумя параметрами и следовательно по МПФ требуется вычислить только две производные и решить полученную систему уравнений. Запишем МПФ для СЭР:

.Выведем формулу для вычисления первого начального момента по первой производной от МПФ:

.Таким образом, получили формулу для вычисления общей интенсивности СЭР:

Выведем формулу для вычисления второго начального момента по второй производной от МПФ:

Запишем формулу для вычисления стандартного отклонения

.

Подставив вместо m₁ и  их оценки m₁^* и ^*, получим формулу для вычисления количества фаз СЭР.

Ф ункция плотности СЭР представлена на рис. 12.7.

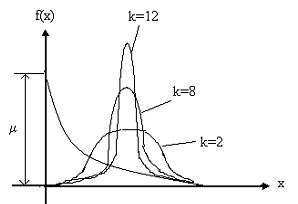
Для СЭР 1, т.к. к>0. Чем больше к, тем меньше отношение и тем более сжато специальное эрланоговское распределение. При к =16 таким распределением можно представить вырожденное распределение, у которого постоянное время задержки.

Область существования специального эрланговского закона представлена на рис.4.8, она расположена ниже экспоненциального закона. Например, при к=2 и m₁=5, σ=3,55.

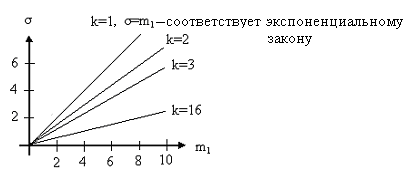При к=3 и m₁=10, σ=5,75. При к=16 и m₁=10, σ=23,5.

Параметры специального эрланговского закона можно вычислить и по упрощенной процедуре, так как математическое ожидание последовательности распределений случайных чисел равно сумме математических ожиданий составляющих эту последовательность, а среднее квадратическое отклонение последовательности сумме средних квадратических отклонений составляющих эту последовательность:

Преобразовав полученные математические выражения и подставив вместо моментов их оценки получим формулы для вычисления параметров специального эрланговского закона, такие же как

.

8. Табличный метод генерации случайных чисел. Достоинства и недостатки.

Т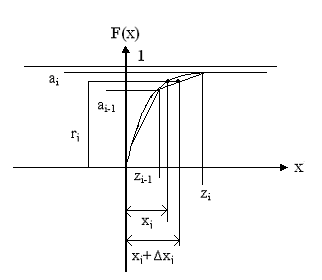 абличный метод основан на том же принципе, что и аналитический, только вместо функции распределения в нём берется ее кусочно-линейное представление, то есть весь диапазон существования распределения случайных чисел разбивается на ряд интервалов, в которых дуги заменяются стягивающими их хордами. Применение метода представлено на рис. Интервал, в который попало случайное число, определяется по выполнению неравенства a_i-1 r_j a_i. На основании подобия треугольников:.

Достоинства и недостатки. 1.этот метод реализуется сравнительно несложными программными процедурами.

2.Табличные методы начинают терять свои позиции и в частности из-за того, что для их применения требуется составление таблиц и выделение памяти для их хранения. В принципе повышение достоверности табличных методов можно достичь увеличением количества интервалов в таблице, но при этом увеличивается время поиска нужного интервала и требуемый объем памяти для хранения таблиц.