2. Метод моментов. Нормальный закон.

Нормальный закон является наиболее употребительным. Он применяется для представления самых различных случайных процессов, таких как продолжительность жизни людей, изменения экономических и технических показателей. Функция плотности нормального закона представляется следующей математической зависимостью:

Характерной особенностью нормального закона является то что в качестве его параметров в функцию плотности входят математическое ожидание и среднее квадратическое отклонение, поэтому для использования метода моментов достаточно в формулу подставить их оценки, вычисленные по экспериментальному распределению. Для оценки качества аппроксимации по критериям согласия Пирсона и Колмогорова требуется вычислить вероятность попадания случайной величины в интервалы гистограммы и гипотетическую ФР. Так как интеграл от функции плотности нормального закона аналитически «не берётся», то он определяется по таблицам, составленным для нормального закона с математическим ожиданием, равным нулю, и средним квадратическим отклонением, равным единице с преобразованием реального распределения по следующим формулам:

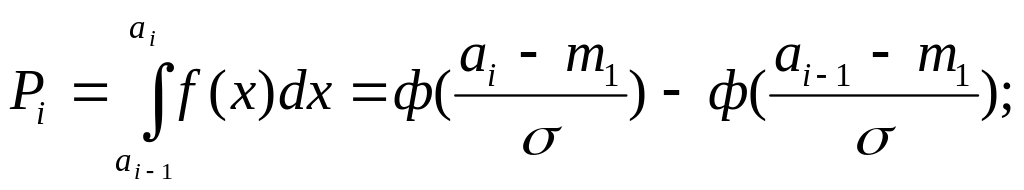
2. Метод моментов. Экспоненциальный закон.

В теории массового обслуживания центральное место занимает экспоненциальный закон, благодаря своим свойствам:

1. Ординарности, которая заключается в том, что если в ОМ действует несколько экспоненциальных законов, то в любой момент времени в такой системе не может произойти более одного события.

2. Стационарности (независимости от времени). Стационарный режим в простейшей системе наступает тогда, когда выполняется условие, что интенсивность поступления транзактов  не превышает интенсивности их обслуживания . В таких системах через некоторое время, которое называют переходным режимом, процесс изменения состояния системы перестает зависеть от времени и зависит только от технических характеристик ОМ и параметров внешней среды, в которой он функционирует. Условие наличия стационарного режима для простейшей СМО

3. Отсутствия последействия, которое заключается в том, что время, оставшееся до окончания экспоненциального процесса в любой момент его протекания распределено по экспоненциальному закону с той же интенсивностью, с которой распределено все распределение случайных чисел.

Эти три свойства позволяют строить Марковские цепи, являющиеся основой аналитического моделирования СМО.

Ф ункция распределения (ФР) экспоненциального закона приведена на рис. Это вероятность того, что случайная величина Х не превысит своего текущего значения х. F(x)

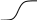
F(x₁) F(x)P{Xx}

x1 х

Функция распределения экспоненциального закона

Ф ункция плотности (ФП). Это плотность вероятности случайной величины, или дифференциальная функция распределения. ФП экспоненциального закона приведена на рис f(x)



f(x)=F^/(x)

x Функция плотности экспоненциального закона

Экспоненциальный закон имеет диапазон своего существования от 0 до . Функция плотности экспоненциального закона .

ФП экспоненциального закона определяется всего одним параметром . Для потоков событий это количество транзактов (заявок), поступающих за единицу времени. Для процессов обслуживания – это количество транзактов, которое может быть обслужено при их непрерывном поступлении в обслуживающий аппарат (ОА). Вычислим первый начальный момент по функции плотности:

Для вычисления интеграла проведём интегрирование по частям:

Пусть , тогда ;

Рассмотрим этот же пример с пределами для определенного интеграла и вычислим основные статистические характеристики экспоненциального закона: Вычислим второй начальный момент: Вычислим среднее квадратическое отклонение