1. ВВЕДЕНИЕ. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ

Процессы принятия решений лежат в основе любой целенаправленной

деятельности. В экономике они предшествуют созданию производственных и

хозяйственных организаций, обеспечивают их оптимальное функционирова-

ние и взаимодействие. В научных исследованиях – позволяют выделить важ-

нейшие научные проблемы, найти способы их изучения, предопределяют

развитие экспериментальной базы и теоретического аппарата. При создании

новой техники – составляют важный этап в проектировании машин, уст-

ройств, приборов, комплексов, зданий, в разработке технологии их построе-

ния и эксплуатации; в социальной сфере – используются для организации

функционирования и развития социальных процессов, их координации с хо-

зяйственными и экономическими процессами. Оптимальные (эффективные)

решения позволяют достигать цели при минимальных затратах трудовых,

материальных и сырьевых ресурсов.

В классической математике методы поиска оптимальных решений рас-

сматривают в разделах, связанных с изучением экстремумов функций, в ма-

тематическом программировании.

Методы оптимальных решений является одним из разделов исследова-

ния операций – прикладного направления кибернетики, используемого для

решения практических организационных задач. Задачи математического про-

граммирования находят применение в различных областях человеческой дея-

тельности, где необходим выбор одного из возможных образов действий

(программ действий).

Значительное число задач, возникающих в обществе, связано с управ-

ляемыми явлениями, т. е. с явлениями, регулируемыми на основе сознатель-

но принимаемых решений. При ограниченном объеме информации, который

был доступен на ранних этапах развития общества, принималось оптималь-

ное решение на основании интуиции и опыта, а затем, с возрастанием объема

информации об изучаемом явлении, – с помощью ряда прямых расчетов. Так

происходило, например, создание календарных планов работы промышлен-

ных предприятий.

Совершенно иная картина возникает, например, на современном про-

мышленном предприятии с многосерийным и многономенклатурным произ-

водством, когда объем входной информации столь велик, что его обработка с 6

целью принятия определенного решения невозможна без применения совре-

менных электронных вычислительных машин. Еще большие трудности воз-

никают в связи с задачей о принятии наилучшего решения.

Под принятием решений в курсе «Методы оптимальных решений» по-

нимают сложный процесс, в котором можно выделить следующие основные

этапы:

1-й этап. Построение качественной модели рассматриваемой пробле-

мы, т. е. выделение факторов, которые представляются наиболее важными, и

установление закономерностей, которым они подчиняются. Обычно этот

этап выходит за пределы математики.

2-й этап. Построение математической модели рассматриваемой про-

блемы, т. е. запись в математических терминах качественной модели. Таким

образом, математическая модель – это записанная в математических симво-

лах абстракция реального явления, так конструируемая, чтобы ее анализ дал

возможность проникнуть в сущность явления. Математическая модель уста-

навливает соотношения между совокупностью переменных – параметрами

управления явлением. Этот этап включает также построение целевой функ-

ции переменных, т. е. такой числовой характеристики, большему (или мень-

шему) значению которой соответствует лучшая ситуация с точки зрения

принимаемого решения.

Итак, в результате этих двух этапов формируется соответствующая ма-

тематическая задача. Причем, второй этап уже требует привлечения матема-

тических знаний.

3-й этап. Исследование влияния переменных на значение целевой

функции. Этот этап предусматривает владение математическим аппаратом

для решения математических, задач, возникающих на втором этапе процесса

принятия решения.

Широкий класс задач управления составляют такие экстремальные за-

дачи, в математических моделях которых условия на переменные задаются

равенствами и неравенствами. Теория и методы решения этих задач как раз и

составляют содержание математического программирования. На третьем

этапе, пользуясь математическим аппаратом, находят решение соответст-

вующих экстремальных задач. Обратим внимание на то, что задачи матема-

тического программирования, связанные с решением практических вопросов,

как правило, имеют большое число переменных и ограничений. Объем вы-7

числительных работ для нахождения соответствующих решений столь велик,

что весь процесс не мыслится без применения современных электронных вы-

числительных машин (ЭВМ), а значит, требует либо создания программ для

ЭВМ, реализующих те или иные алгоритмы, либо использования уже имею-

щихся стандартных программ.

4-й этап. Сопоставление результатов вычислений, полученных на 3-м

этапе, с моделируемым объектом, т. е. экспертная проверка результатов (кри-

терий практики). Таким образом, на этом этапе устанавливается степень аде-

кватности модели и моделируемого объекта в пределах точности исходной

информации. Здесь возможны два случая:

1-й случай. Если результаты сопоставления неудовлетворительны

(обычная ситуация на начальной стадии процесса моделирования), то пере-

ходят ко второму циклу процесса. При этом уточняется входная информация

о моделируемом объекте и, в случае необходимости, уточняется постановка

задачи (1-й этап); уточняется или строится заново математическая модель

(2-й этап); решается соответствующая математическая задача (3-й этап) и,

наконец, снова проводится сопоставление (4-й этап).

2-й случай. Если результаты сопоставления удовлетворительны, то мо-

дель принимается. Когда речь идет о неоднократном использовании на прак-

тике результатов вычислений, возникает задача подготовки модели к экс-

плуатации. Предположим, например, что целью моделирования является соз-

дание календарных планов производственной деятельности предприятия. То-

гда эксплуатация модели включает в себя сбор и обработку информации,

ввод обработанной информации в ЭВМ, расчеты на основе разработанных

программ календарных планов и, наконец, выдачу результатов вычислений (в

удобном для пользователей виде) для их использования в сфере производст-

венной деятельности.

В математическом программировании можно выделить два направле-

ния.

К первому, уже вполне сложившемуся направлению – собственно ма-

тематическому программированию – относятся детерминированные задачи,

предполагающие, что вся исходная информация является полностью опреде-

ленной.

Ко второму направлению – так называемому стохастическому про-

граммированию – относятся задачи, в которых исходная информация содер-8

жит элементы неопределенности, либо когда некоторые параметры задачи

носят случайный характер с известными вероятностными характеристиками.

Так, планирование производственной деятельности зачастую производится в

условиях неполной информации о реальной ситуации, в которой будет вы-

полняться план. Или, скажем, когда экстремальная задача моделирует работу

автоматических устройств, которая сопровождается случайными помехами.

Заметим, что одна из главных трудностей стохастического программирова-

ния состоит в самой постановке задач, главным образом из-за сложности

анализа исходной информации.

Традиционно в математическом программировании выделяют следую-

щие основные разделы:

Линейное программирование – целевая функция линейна, а множество,

на котором ищется экстремум целевой функции, задается системой линейных

равенств и неравенств. В свою очередь в линейном программировании суще-

ствуют классы задач, структура которых позволяет создать специальные ме-

тоды их решения, выгодно отличающиеся от методов решения задач общего

характера. Так, в линейном программировании появился раздел транспорт-

ных задач.

Нелинейное программирование – целевая функция и ограничения нели-

нейны. Нелинейное программирование принято подразделять следующим

образом:

Выпуклое программирование – целевая функция выпукла (если рас-

сматривается задача ее минимизации) и выпукло множество, на котором ре-

шается экстремальная задача.

Квадратичное программирование – целевая функция квадратична, а

ограничениями являются линейные равенства и неравенства.

Многоэкстремальные задачи. Здесь обычно выделяют специализиро-

ванные классы задач, часто встречающихся в приложениях, например, задачи

о минимизации на выпуклом множестве вогнутых функций.

Важным разделом математического программирования является цело-

численное программирование, когда на переменные накладываются условия

целочисленности.

Целью математического программирования является создание, где это

возможно, аналитических методов определения решения, а при отсутствии 9

таких методов – создание эффективных вычислительных способов получения

приближенного решения.

Наконец, заметим, что наименование предмета – ―методы оптимальных

решений‖ – связано с тем, что целью решения задач является выбор про-

граммы действий. Рассмотрим более подробно задачу линейного программи-

рования.

2. УСЛОВНЫЙ ЭКСТРЕМУМ- минимальное или максимальное значение, достигаемое данной функцией (или функционалом) при условии, что нек-рые другие функции (функционалы) принимают значения из заданного допустимого множества. Если условия, ограничивающие в указанном смысле область изменения независимых переменных (функций), отсутствуют, то говорят о безусловном экстремуме.  Классич. задачей на У. э. является задача определения минимума функции многих переменных

  при условии, что нек-рые другие функции принимают заданные значения:

В этой задаче множество G, к-рому должны принадлежать значения вектор-функции g=(g₁, ...,g_m), входящей в дополнительные условия (2), есть фиксированная точка c=(c₁, ..., с _т )в m-мерном евклидовом пространстве    Если в (2) наряду со знаком равенства допускаются знаки неравенства

  то это приводит к задаче нелинейного программирования(1), (3). В задаче (1), (3) множество Gдопустимых значений вектор-функции gпредставляет собой нек-рый криволинейный многогранник, принадлежащий (n-m₁ )-мерной гиперповерхности, задаваемой т ₁, m₁<n, условиями типа равенства (3). Границы указанного криволинейного многогранника строятся с учетом п-m₁неравенств, входящих в (3).  Частным случаем задачи (1), (3) на У. в. является задача линейного программирования, в к-рой все рассматриваемые функции f иg_i являются линейными по x_l, ... , х _п. В задаче линейного программирования множество Gдопустимых значений вектор-функции g,входящей в условия, ограничивающие область изменения переменных x₁, .....x_n, представляет собой выпуклый многогранник, принадлежащий (п-т ₁ )-мерной гиперплоскости, задаваемой m₁ условиями типа равенства в (3).  Аналогичным образом большинство задач оптимизации функционалов, представляющих нрактич. интерес, сводится к задачам на У. э. (см. Изопериметрическая задача, Кольца задача, Лагранжа задача, Манера задача). Так же, как и в математич. программировании, основными задачами вариационного исчисления и теории оптимального управления являются задачи на У. э.  При решении задач на У. э., особенно при рассмотрении теоретич. вопросов, связанных с задачами на У. э., весьма полезным оказывается использование неопределенных Лагранжа множителей, позволяющих свести задачу на У. э. к задаче на безусловный экстремум и упростить вывод необходимых условий оптимальности. Использование множителей Лагранжа лежит в основе большинства классич. методов решения задач на У. э.

Геометрический смысл условного экстремума функции:

Условными экстремумами функции z = f(x,y) при F(x,y) = 0 являются ее экстремумы на линии, образующейся в сечении поверхности z = f(x,y) цилиндрическойповерхностью F(x,y) = 0 .

4. Постановка задачи оптимизации

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называетсяпараметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ^*, который доставляет минимальное значение f(χ^*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

1. Допустимое множество — множество  ;

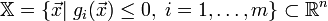2. Целевую функцию — отображение  ;

3. Критерий поиска (max или min).

Тогда решить задачу   означает одно из:

1. Показать, что  .

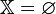2. Показать, что целевая функция   не ограничена снизу.

3. Найти  .

4. Если  , то найти  .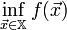

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек   таких, что всюду в некоторой их окрестности   для минимума и   для максимума.

Если допустимое множество  , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации

Исходные данные	Переменные	Зависимости	Задача
Детерминированные	Непрерывные	Линейные	Линейного программирования
	Целочисленные	Линейные	Целочисленного программирования
	Непрерывные, целочисленные	Нелинейные	Нелинейного программирования
Случайные	Непрерывные	Линейные	Стохастическое программирование

А по критерию эффективности:

одноцелевое принятие решений (один критерий эффективности);

многоцелевое принятие решений (несколько критериев эффективности).

Наиболее разработан и широко используется на практике аппарат одноцелевого принятия решений в условиях определенности, который получил название математического программирования. В этом "детерминированном" случаи, когда все условия операции известны заранее. тогда, обратная задача будет включает в себя критерий эффективности и некоторые известные заранее факторы (ограничения) позволяющие выбрать множество допустимых решений.

В общем виде обратная детерминированная задача будет выглядеть следующим образом.

При заданном комплексе ограничений найти такое оптимальное решение, принадлежащее множеству допустимых решений, которое обращает критерий эффективности в максимум (минимум).

Метод поиска экстремума и связанного с ним оптимального решения должен всегда исходить из особенности критерия эффективности и вида ограничений, налагаемых на решение.

Очень часто реальные задачи содержит помимо выше перечисленных факторов, еще одну группу - неизвестные факторы. Тогда обратную задачу можно сформулировать следующим образом.

При заданном комплексе ограничений, с учетом неизвестных факторов, найти такое оптимальное решение, принадлежащее множеству допустимых решений, которое, по возможности, обеспечивает максимальное (минимальное) значение критерий эффективности.