Замена переменных в тройном интеграле.
,
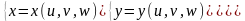где |I| - модуль
Якобина.
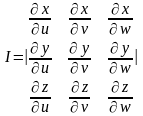Геометрический смысл: |I|
-коэффициент растяжения объёма при
отображении области V
на область V’
В цилиндрических координатах:
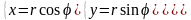
В сферических координатах:
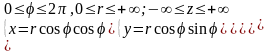
Билет 35.
Поверхностный интеграл1-го рода (ПОВИ-1).
,
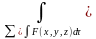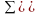-гладкая(в
каждой точке существует касательная
плоскость). Пусть
такова, что прямая параллельная OZ
пересекает её не более чем в 1-ой точке.
Тогда z=f(x,y);
Поверхностный интеграл 1-го рода (Пови-1)
Сведение к двойному
1. Поверхность s задана уравнением
где
-
величина угла между нормалью к поверхности
и положительным направлением оси Oz.
2. Поверхность s задана параметрически:
где
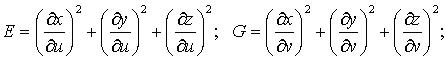
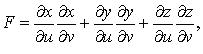или
где
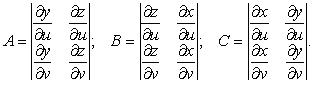
Билет 36.
Интеграл по ориентированной фигуре от векторной ф-ции.
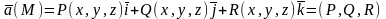
Векторная ф-ция 3х переменных x,y,z,
определенной на фигуре Ф. Ф-ции P,Q,R
называются координатами
.
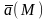Фигура Ф называется ориентированной,
если в каждой ее точке М задан некоторый
вектор
,
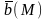характеризующий эту фигуру. Диния
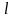называется ориентированной, если на
ней выбрано направление перемещения.
Гладкая поверхность называется двусторонняя, если нормаль к ней при обходе по замкнутому контуру, лежащему на поверхности и не имеющему общих точек с ее границей, возвращается к своему первоначальному положению.
1).
;
2).
;
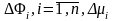3).
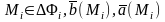; 4).
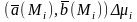
5).
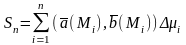; n-я интегральная
сумма для векторной ф-ции a(M)
по ориентированной с помощью вектора
P(n)
фигуре Ф. ; 6).
(*)
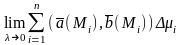Если (*) существует, конечен и не зависит от способа построения интегральной суммы , то он называется интегралом по орентированной фигуре Ф от векторной ф-ции a(M).
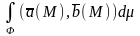
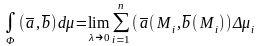
P(x,y,z) Q(x,y,z) R(x,y,z) a=(P,Q,R)
Если ф-ции P,Q,R непрерывны на гладкой, ограниченной, содержащей граничные точки ориентированной фигуре Ф, то интеграл существует.
Частные случаи интегралов по ориентированной фигуре.
Свойства интеграла по фигуре от векторной ф-ции.
1).
;
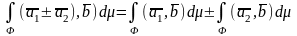2).
,
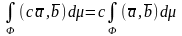c=const
3).
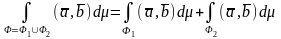; 4).
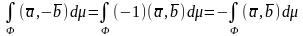
Билет 37
Механический смысл КРИ-2:
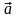(М)
– вектор силы; L=AB;
Работа силы по перемещению вдоль L.
Если
(М)
– переменная сила, а AB
– кривая, то:
-
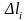настолько малы, что перемещение на
кусочек по направлению совпадает с
единичным касательным вектором.
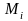-произвольная
точка.
(
)
– постоянная сила.
=(
(
),
)=(
(
),
)
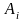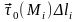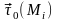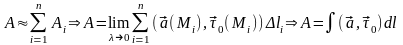
!!! С механической точки зрения КРИ-2 представляет собой работу силы вдоль линии L.
Скалярная форма кри-2
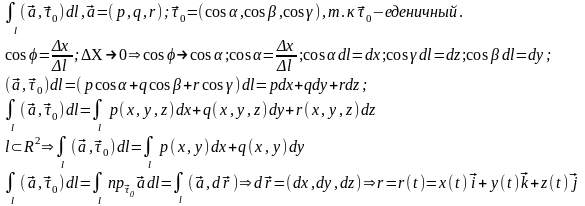
Вычисление КРИ-2
,
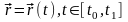
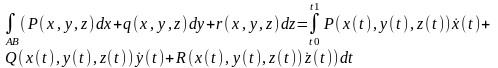
Вывод: в общем случае КРИ-2 зависит от пути интегрирования.
Билет 38.
Формула Грина.
Область наз. односвязной если в ней любой замкнутый контур может быть стянут в точку с помощью непрерывной деформации, при к-й не границы области не пересекаютя.
Область D наз. односвяз., если каков бы ни был замкн. контур l , лежащий внутри этой области, ограниченная этим контуром конечн. часть пл-ти целиком принадл. D.
Порстая область: замкн. пл-ть D (обл. вместе с её границами) – её можно разбить на конечное число как y- так и x- трапецивидных областей.
Например: круг, прямоугольник, кольцо.
Теор. Грина: пусть P(x,y),
Q(x,y)
и
и
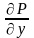непрерывны в простой области D
тогда
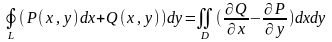
где L – граница области D, к-я обходится в положительном направлении.
Док-во
Предположим D – односвяз. область, огр. L – полож. ориентир. Предположим, что оюл. D такова, что прямые параллельн. осям пересекают ее не более, чем в 2-х точках.
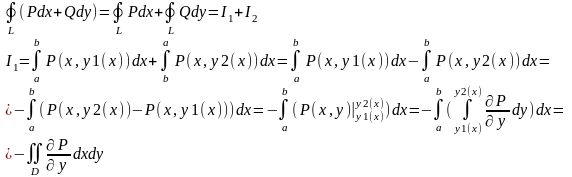
Для I2 – аналогично.
Формула Грина имеет место для любой простой области.
Если контур обходится в обратном направлении, то перед двойным интегралом ставится «-».