Магнитные свойства вещества

1.  Диамагнетики —      чуть <1. _{висмута}=0,9998 (свинец, цинк, азот и др.).

2. Парамагнетики —  чуть>1. _{алюминия}=1,000023 (кислород, ни­кель и др.).

Для пара- и диамагнетиков намагниченность I прямо пропорциональна индук­ции B₀ магнитного поля в вакууме.

3. Ферромагнетики—  >>1. _стали = 8^.10³ (железо, никель, кобальт и их сплавы). Сплав железа с никелем:  =2,5^.10⁵.

49. Магнитная проницаемость — физическая величина, характеризующая связь между магнитной индукцией B и магнитным полем H в веществе.

Отношение B/H=μ_a называется абсолютной магнитной проницаемостью среды.

Численное значение μ_a (абсолютная магнитная проницаемость) выражают в относительных единицах (по отношению к абсолютному значению магнитной проницаемости вакуума μ_о). Величина μ=μ_a/μ_о называется относительной магнитной проницаемостью (или просто магнитной проницаемостью). Она не зависит от выбора систем единиц.

Ферромагнетики - это вещества, обладающие спонтанной намагниченностью, то есть они сохраняют намагниченность при отсутствии внешнего магнитного поля.

К ферромагнетикам относятся, например, кристаллы железа, никеля, кобольта.

Ферромагнетики - это вещества, обладающие спонтанной намагниченностью, то есть они сохраняют намагниченность при отсутствии внешнего магнитного поля.

К ферромагнетикам относятся, например, кристаллы железа, никеля, кобольта.

50. Магнитный поток.

В однородном магнитном поле, модуль вектора индукции которого равен В, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол a с направлением вектора магнитной индукции В. Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:

Φ = B · S · cos α

Единица измерения магнитного потока в систем СИ - 1 Вебер (1 Вб).

1 Вб = 1 Тл · 1 м²

Магнитный поток через контур максимален,если плоскость контура перпендикулярна магнитному полю. Значит угол a равен 0⁰ . Тогда магнитный поток рассчитывается по формуле:

Φ_max = B · S

Магнитный поток через контур равен нулю,если контур распологается параллельно магнитному полю. Значит угол a равен 90⁰ .

51. Электромагнитная индукция.

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Электромагнитная индукция была открыта Майклом Фарадеем . Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.

52. ЭДС индукции. Закон электромагнитной индукции .

ЭДС (ε) - отношение работы сторонних сил по разделению зарядов к величине этого заряда, иначе, способность данного источника давать необходимое количество зарядов необходимой энергии. - ЭДС. ЭДС не является силой в Ньютоновом смысле (неудачное название величины, сохраненное как дань традиции). ε_i возникает при изменении магнитного потока Ф, пронизывающего контур. 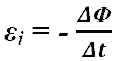-ЭДС индукции. - ЭДС индукции 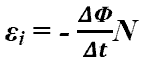в контуре, содержащем N витков провода. - ЭДС индукции при движении одного из проводников контура (так, чтобы менялся Ф). В этом случае проводник длиной l, движущийся со скоростью v становится источником тока. - ЭДС индукции в контуре, вращающемся в магнитном поле со скоростью ω. Другие формулы, где встречается ЭДС: -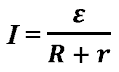 закон Ома для полной цепи. В замкнутой цепи ЭДС рождает электрический ток I.

53.Правило Ленца. Вихревое электрическое поле.

Правило Ленца определяет направление индукционного тока, возникающего в результате электромагнитной индукции.

Если металлический проводник передвигается вблизи гальванического тока или вблизи магнита, то в нем возбуждается гальванический ток такого направления, которое вызывало бы движение покоящегося провода в направлении, прямо противоположном направлению движения, навязанного здесь проводу извне, в предположении, что находящийся в покое провод может двигаться только в направлении этого последнего движения или прямо противоположном. Правило Ленца основано на обобщении опытов по электромагнитной индукции.

В сжатой форме правило Ленца можно сформулировать так:

возникающий в замкнутом проводнике индукционный ток имеет такое направление, чтобы препятствовать изменению потока магнитной индукции, которое его вызывает.

Вихревое электрическое поле это индуцированное электрическое поле. Переменное магнитное поле порождает наведенное (индуцированное) электрическое поле. Если магнитное поле постоянно, то индуцированного электрического поля не возникает. Следовательно, индуцированное электрическое поле не связано с зарядами, как в случае электростатического поля; его силовые линии не начинаются и не заканчиваются на зарядах, а замкнуты сами на себя, подобно силовым линиям магнитного поля.

54.  Явление самоиндукции заключается в появлении ЭДС индукции в самом проводнике при изменении тока в нем. Примером явления самоиндукции является опыт с двумя лампочками, подключенными параллельно через ключ к источнику тока, одна из которых подключается через катушку (рис. 39). При замыкании ключа лампочка 2, включенная через катушку, загорается позже лампочки 1. Это происходит потому, что после замыкания ключа ток достигает максимального значения не сразу, магнитное поле нарастающего тока породит в катушке индукционную ЭДС, которая в соответствии с правилом Ленца будет мешать нарастанию тока.           Для самоиндукции выполняется установленный опытным путем закон: ЭДС самоиндукции прямо пропорциональна скорости изменения тока в проводнике. .

55. ЭДС САМОИНДУКЦИИ. Индуктивность.

Э ДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи. Индуктивность - физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду. Также индуктивность можно рассчитать по формуле:

где Ф - магнитный поток через контур, I - сила тока в контуре.

56. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА

Вокруг проводника с током существует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля. Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.

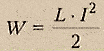
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? - выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры

Таким образом, энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, равна

57.Колебательное движение. Амплитуда, частота, фаза и период колебания.

Любое колебательное движение характеризуется амплитудой А - максимальным отклонением колеблющейся точки от положения равновесия. Колебания точки, происходящие с постоянной амплитудой, называют незатухающими, а колебания с постепенно уменьшающейся амплитудой - затухающими.

Время, в течение которого совершается полное колебание, называют периодом Т.

Частотой v периодических колебаний называют число полных колебаний, совершаемых за единицу времени. Единица частоты колебаний - герц (Гц).

число колебаний за 2π секунд: ω = 2πν = 2π/ T. Размерность [ω] = 1Гц.

58. Пружинный и математический маятник. Превращение энергии при гармонических колебаниях.

1. Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид или Из формулы (1) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω₀t+φ) с циклической частотой (2) и периодом Формула (3) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника (8) , где l — длина маятника. Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то, подставив (8) в (7), найдем выражение для периода малых колебаний математического маятника 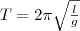Пусть колебание происходит по закону синуса , тогда скорость меняется по закону косинуса . Запишем выражение для кинетической энергии: .

  Согласно закону сохранения энергии, полная энергия будет равна максимальной кинетической, т.к. в положении равновесия потенциальная равна нулю.

59. Графическое представление гармонических колебаний. Сложение гармонических колебаний.

Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис. 2.1.1).