27. Неравенство Чебышева. Теорема Чебышева (закон больших чисел).

Нера́венство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего. Неравенство Чебышёва является следствиемнеравенства Маркова.

   (обобщённое неравенство Чебышёва). Пусть функция   не убывает и неотрицательна на  . Если  , то для любого 

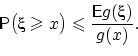
Доказательство. Заметим, что  , поскольку функция   не убывает. Оценим последнюю вероятность согласно неравенству Маркова, которое можно применять в силу неотрицательности  :

Пусть имеется случайная величина   с математическим ожиданием   и дисперсией  . Неравенство Чебышева утверждает, что, каково бы ни было положительное число  , вероятность того, что величина   отклонится от своего математического ожидания не меньше чем на  , ограничена сверху величиной  :

.                                  (13.2.1)

Доказательство. 1. Пусть величина   прерывная, с рядом распределения

Изобразим возможные значения величины   и ее математическое ожидание   в виде точек на числовой оси   (рис. 13.2.1).

Рис. 13.2.1.

Зададимся некоторым значением   и вычислим вероятность того, что величина   отклонится от своего математического ожидания не меньше чем на  :

.                               (13.2.2)

Для этого отложим от точки   вправо и влево по отрезку длиной  ; получим отрезок  . Вероятность (13.2.2) есть не что иное, как вероятность того, что случайная точка   попадет не внутрь отрезка  , а вовне его:

.

Для того чтобы найти эту вероятность, нужно просуммировать вероятности всех тех значений  , которые лежат вне отрезка  . Это мы запишем следующим образом:

 (13.2.3)

где запись   под знаком суммы означает, что суммирование распространяется на все те значения  , для которых точки  , лежат вне отрезка  .

С другой стороны, напишем выражение дисперсии величины  . По определению:

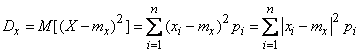.   (13.2.4)

Так как все члены суммы (13.2.4) неотрицательны, она может только уменьшиться, если мы распространим ее не на все значения  , а только на некоторые, в частности на те, которые лежат вне отрезка  :

.               (13.2.5)

Заменим под знаком суммы выражение   через  . Так как для всех членов суммы  , то от такой замены сумма тоже может только уменьшиться; значит,

.             (13.2.6)

Но согласно формуле (13.2.3) сумма, стоящая в правой части (13.2.6), есть не что иное, как вероятность попадания случайной точки вовне отрезка  ; следовательно,

,

откуда непосредственно вытекает доказываемое неравенство.

2. В случае, когда величина непрерывна, доказательство проводится аналогичным образом с заменой вероятностей элементом вероятности, а конечных сумм - интегралами. Действительно,

.                (13.2.7)

где   - плотность распределения величины  . Далее, имеем:

,

где знак   под интегралом означает, что интегрирование распространяется на внешнюю часть отрезка  .

Заменяя   под знаком интеграла через  , получим:

,

откуда и вытекает неравенство Чебышева для непрерывных величин.

Пример. Дана случайная величина   с математическим ожиданием   и дисперсией  . Оценить сверху вероятность того, что величина   отклонится от своего математического ожидания не меньше чем на  .

Решение. Полагая в неравенстве Чебышева  , имеем:

,

т. е. вероятность того, что отклонение случайной величины от ее математического ожидания выйдет за пределы трех средних квадратических отклонений, не может быть больше  .

Примечание. Неравенство Чебышева дает только верхнюю границу вероятности данного отклонения. Выше этой границы вероятность не может быть ни при каком законе распределения. На практике в большинстве случаев вероятность того, что величина   выйдет за пределы участка  , значительно меньше  . Например, для нормального закона эта вероятность приблизительно равна 0,003. На практике чаще всего мы имеем дело со случайными величинами, значения которых только крайне редко выходят за пределы  . Если закон распределения случайной величины неизвестен, а известны только   и  , на практике обычно считают отрезок   участком практически возможных значений случайной величины (так называемое «правило трех сигма»)