
- •25. Некоторые законы распределения непрерывных случайных величин: экспоненциальное распределение.
- •26. Некоторые законы распределения непрерывных случайных величин: нормальное распределение.
- •27. Неравенство Чебышева. Теорема Чебышева (закон больших чисел).
- •2. В случае, когда величина непрерывна, доказательство проводится аналогичным образом с заменой вероятностей элементом вероятности, а конечных сумм - интегралами. Действительно,
- •Формулировка теоремы Чебышева
25. Некоторые законы распределения непрерывных случайных величин: экспоненциальное распределение.
Экспоненциальное распределение и его свойства Экспоненциальное распределение играет важную роль в задачах телекоммуникации, так как позволяет моделировать интервалы времени между наступлением событий. Из экспоненциальных величин строятся другие важные величины, например, случайные величины, имеющие распределение Эрланга. Мы
говорим, что случайная
величина
Пусть
-
время ожидания события, тогда из
формулы (0) следует, что вероятность
того, что это событие наступит раньше
x равна Параметр λ оценивается на основе реальных данных. Плотность экспоненциального распределения имеет вид
где λ>0 —положительная постоянная, называемая параметром экспоненциального распределения. Заметьте, экспоненциальное распределение сосредоточено на положительной полуоси. Экспоненциальная случайная величина принимает положительные значения. Среднее
значение
равно
Дисперсия
равна
Из формулы (0) следует:
Иными
словами, вероятность того, что следующее
событие наступит через время больше Основные свойства экспоненциального распределения 1. Отсутствия последействия. Пусть — экспоненциальная случайная величина с плотностью вида (1). Тогда
при всех x≥0 и t≥0. Равенство (2) означает следующее. Пусть некоторая элементарная операция (например, телефонный разговор) имеет случайную длительность с экспоненциальным распределением. Пусть,
далее, известно, что до момента Тогда остаток от момента до момента окончания операции имеет экспоненциальное распределение с параметром λ независимо от t. Это важнейшее свойство экспоненциального распределения называется отсутствием последействия. Отсутствие последействия называется также Марковским свойством. Именно в силу этого свойства экспоненциальные модели имеют довольно простое аналитическое решение. 2.
При малых положительных h Действительно, по формуле Тейлора имеем:
Равенство (3) можно объяснить так. Пусть в момент длится некоторая операция, имеющая случайную длительность с плотностью задаваемой формулой (1). Тогда
вероятность окончания данной операции
в данном интервале ( t0,
t0+h)
равна 3. Пусть в момент длятся n операций. Рассмотрим
случайные величины Если
величины
независимы
и имеют экспоненциальное распределение
с параметрами а) б)
если известно, что 1≤i≤n Доказательство. Имеем
— свойство а) доказано. Далее,
Однако
В
то же время Подставим выражения (6) и (7) в равенство (5), получим формулу (4). Таким образом, утверждение б) также доказано. 4. Пусть выполнены те же условия, что и в формулировке предыдущего свойства.
Обозначим
через Тогда
Доказательство.
Событие (
т.е. справедливость формулы (8) доказана. Событие
(
Далее
можно записать
— формула (9) доказана. Наконец, откуда Подставляя в это равенство соотношения (9) и (10), найдем
Справедливость формулы (11) так же установлена. При доказательстве формул дважды использована формула
Разумеется,
следует проверить несовместимость
событий В рассмотренных случаях она непосредственно очевидна. 5. Пусть выполнены условия предыдущего пункта и в момент окончания i-ой операции начинается одна или несколько новых операций, длительности которых независимы между собой, не зависят от ( ) и имеют экспоненциальное распределение. Тогда
если обозначить через Для
доказательства, в дополнении к
предыдущему, остаточно заметить, что
событие ( Имеем где 6. Пусть операция начинается в момент t0 и состоит в выполнении некоторой случайной работы , причем темп выполнения работы в момент t равен ά(t), t≥t0 , где ά(t) — интегрируемая неотрицательная функция. Обозначим
через Тогда если случайная величина распределена по экспоненциальному закону с параметром λ, то
Доказательство. За
время от t0 до
t0+t
может быть выполнено
Значит,
операции закончится за время, меньше
t, при условии что Таким образом,
|

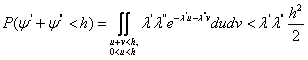 ,
, (12)
(12)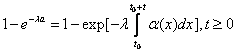 ,
,
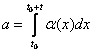 ед.
работы.
ед.
работы.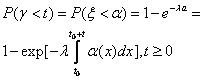 .
.