4. Геом. Смысл

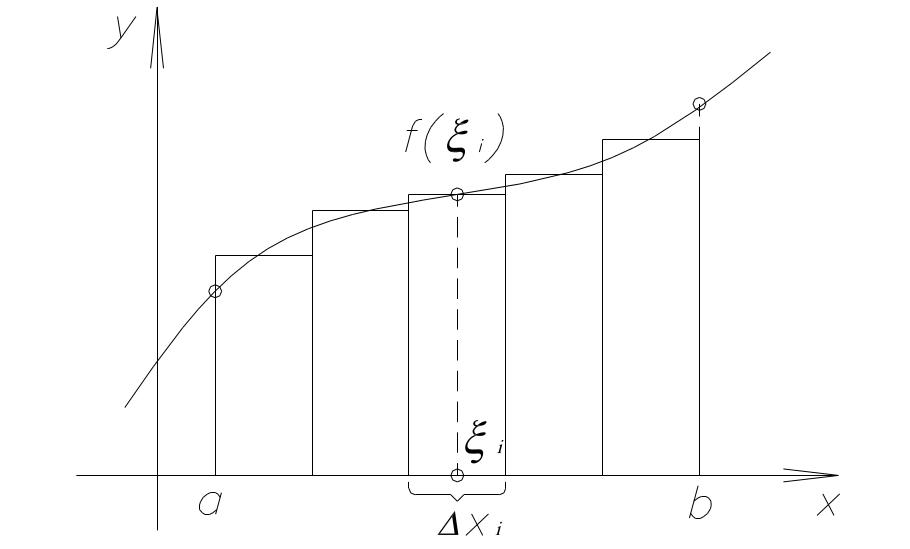
S – площадь криволинейной трапеции, ограниченной сверху графиком функции y = f(x) ,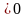

снизу – осью ОХ, слева – вертикальной прямой х = а, справа – вертикальной прямой х = b.

Физ. Смысл

1. 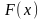− сила, параллельная оси 0Х и ориентированная в положительном направлении оси 0Х, действующая на материальную точку при прямолинейном перемещении по промежутку [a, b]. Работа А силы при этом равна: .

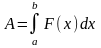2. 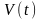− скорость неравномерного прямолинейного движения материальной точки.

Путь 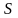, пройденный точкой за промежуток времени ,

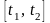при этом равен: .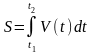

3. 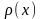− плотность неоднородного прямолинейного стержня с концами в точках .

Масса m такого стержня равна: .

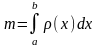^6. Теорема: (Теорема Ньютона – Лейбница)

Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то

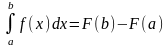
это выражение известно под названием формулы Ньютона – Лейбница.

Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция 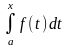- первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то

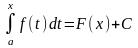
при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:

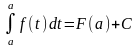
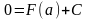
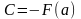
Тогда .

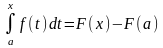А при х = b:

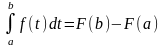
Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:

Теорема доказана.

_5. Теорема о среднем значении

Если функция f(x) непрерывна на отрезке [a;b], то существует точка   такая, что  .

Док-во: По формуле Ньютона-Лейбница имеем

, где F’(x)=f(x). Применяя к разности F(b)-F(a) теорему Лагранжа (теорему о конечном приращении функции), получим F(b)-F(a)=F’(c)*(b-a)=f(c)*(b-a).

Эта теорема при f(x) 0 имеет простой геометрич. смысл: значение определенного интег-ла равно, при нек-ром  , площади прямоугольника с высотой f(с) и основанием b-a.

Число   наз-ся средним значением функции f(x) на отрезке [a;b].

Теорема Барроу

_{x x}

∫f(t)*dt=F(x) ( ∫f(t)*dt)’=f(x)

^{a a}

производная интеграла с переменным верхним пределом равна ф-ции от верхнего предела

_x+Δx

F(x+Δx)= ∫f(t)*dt

_x ^a _{b x}

( ∫f(t)*dt)’=lim (F(x+Δx)-F(x))/ Δx=lim( ∫f(t)*dt - ∫f(t)*dt )/Δx=

^a _x ^Δx0_{x+Δx x} ^{Δx0 a a}

=lim (∫f(t)*dt + ∫f(t)*dt - ∫f(t)*dt )/Δx=lim (f(c)*Δx)/Δx=lim f(c)

^{Δx0 a x a Δx0 Δx0}

То lim f(c)=f(x)

^Δx0

7. Формула интегрирования по частям в определенном интегралеТеорема:Пусть функции u=u(x) и v=v(x) имеют на отрезке [a,b] непрерывные производные u`(x) и v`(x). Тогда имеет место равенство

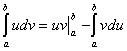
В силу условия теоремы произведение uv=u(x)v(x) данных функций имеет на [a,b] производную, равную

(uv)`=uv`+vu`, т.е. является первообразной на [a,b] для функции uv`+vu`. Применяя формулу Ньютона-Лейбница, получим

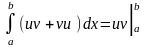. Отсюда находим

Так как по определению дифференциала функции v`dx=dv, u`dx=du то окончательно будем иметь

Замена переменных в определенном интеграле.

Теорема 1 (внесение множителя под знак дифференциала): Пусть u=(x) непрер. дифференцируема на пром-ке с концами a и b; пусть f(u) непрер. на множ-ве значений u=(x) Е().

Тогда 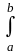f((x)) (х)dx=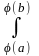 f(u)du

Док-во: если f(u) имеет первообр. F(u), то f((x)) (х) имеет первообр. F( (x))

f((x)) (х)dx= F( (x)) |^b_a= F( (b)) - F( (a)); f(u)du=F(u) |^(b)_(a)= F( (b)) - F( (a)) ч.т.д.

Теорема 2 (вынесение множителя из-под знака диф-ла): Пусть х=(t) непрер. диф-ма на (,); (t)>0 (=> возрастает) ((t)<0); ()=a; ()=b; пусть f(x) непрер. на пром-ке с концами a и b, тогда

f(х)dх=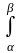 f((t)) (t)dt

Док-во: g(t)= f((t)) (t); если g(t) имеет первообр. G(t) на (a,b), то f(x) имеет первообр. F(x)=G(^-1(x)) (сущ-ние ^-1(x) гарантировано монотонностью: ^-1(x)>0 (<0)); f((t)) (t)dt= G(t) |^_=G() – G()

f(х)dх=G(^-1(x)) |^b_a=G(^-1(b)) - G(^-1(a))= G() - G() ч.т.д.