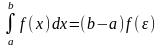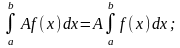1. Вычисление площадей плоских фигур.

А) Площадь криволинейной трапеции, ограниченной кривой y=f(x) [f(x) ≥ 0], прямыми x=a и x=b и отрезками [a; b] оси Ох, вычисляется по формуле:

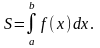
Площадь фигуры, ограниченной кривыми y=f₁(x) и y=f₂(x)[f₁(x) ≤ f₂(x)] и прямыми x=a и x=b, находится по формуле:

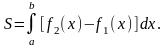
Если кривая задана параметрическими уравнениями x=x(t), y=y(t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b и отрезком [a; b] оси Ох, выражается формулой:

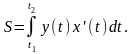
где t₁ и t₂ определяются из уравнений a=x(t₁), b=x(t₂) [y(t) ≥ 0 при t₁ ≤ t ≤ t₂].

Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением ρ=ρ(θ) и двумя полярными радиусами θ=α, θ=β (α < β), выражается интегралом:

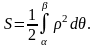
Б)Дан линейный неоднородный стержень, лежащий на оси   в пределах отрезка  . Требуется определить массу этого стержня. Пусть плотность распределения массы вдоль стержня есть некоторая непрерывная функция от  :  .

Для определения массы стержня разобьем его на   произвольных частей точками  . В пределах каждой части   выберем по произвольной точке  .

Так как в пределах   функция   изменяется мало, то массу части стержня, соответствующей отрезку  , можно считать приближенно равной  , где  .

Масса же   всего стержня  приближенно равна

{

}

Точное значение массы, очевидно, получим в пределе, когда наибольший частичный отрезок стремится к нулю, т. е.

2. Определение интеграла по фигуре.

Пусть дана фигура G , р  текущая точка на фигуре.

f(p)  заданная на фигуре G

Выполним след. операции:

1.Разобьем G на куски: G₁, G₂,…, G_n,  меры кусков.

2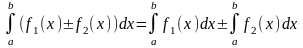 .Внутри каждого куска выберем по 1 точке р1, р2, р3…

3.Вычисляем значение функции в выбранных точках

4.Составляем сумму произведений

f(p₁)* G₁+ f(p₂)* G₂+… +f(p_n)* G_n=(n/i=1)f(p_i)*G_i 

эта сумма называется интегральной суммой функции f(p) по фигуре G при разбиениии n

Опр. Интегралом по фигуре G функции f(p) называется предел интегральных сумм этой функции, когда n0

_Gf(p)dG=Lim(n)*(n/i=1)f(P_i)*G_i

Если этот предел существует и независит от способов разбиения при условии, что диаметры кусков при этом стремятся к нулю.

Диаметром куска называется его максимальный линейный размер.

Max dim G 0

Cвойства интеграла по фигуре.

1.Итеграл по фигуре от единичной функции равен мере фигуры.

_GdG=G  мера фигуры

Док-во: по определению

_GdG=Lim(n)*(n/i=1)1*G=G  как сумма мер всех кусков.

3. Свойства определенного интеграла.

1. 

3)

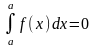
4. Если f(x)  (x) на отрезке [a, b] a < b, то

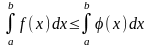
4. Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

4. Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка  такая, что