12. Волновая функция микрочастицы и ее свойства. Стационарное и нестационарное уравнение Шредингера.

Волновая функция имеет статистический смысл: квадрат модуля волновой функции определяет плотность вероятности нахождения частицы (электрона): dw/dV = |Ψ|².

Здесь dw вероятность нахождения частицы в элементе объема от V до V+dV.

Свойства волновой функции:

1) Правило нормировки:

Правило выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией во всем пространстве равна единице.

2) Импульс частицы в каждом из направлений x, y, z пропорционален первой производной волновой функции, делённой на саму волновую функцию, а именно:

           

где p_x , p_y , p_z — проекции импульсов на соответствующие оси координат, i = √-1 - мнимая единица, ħ = h/2π - постоянная Планка.

3) Кинетическая энергия частицы (p²_x + p²_y + p²_z) / 2m пропорциональна второй производной, или кривизне волновой функции, деленной на эту волновую функцию .

Стационарное уравнение Шредингера для движения электрона в кулоновском поле ядра атома водорода и водородоподобных атомов имеет вид: ∆ψ + (8π²m/h²)(E-U)Ψ = 0,

где Ψ – волновая функция, ∆ - оператор Лапласа, Е – полная энергия электрона в атоме, U = -(Ze²/4πε₀r) – потенциальная энергия.

Уравне́ние Шрёдингера — уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемоговолновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнениевторого закона Ньютона в классической механике. Его можно назвать уравнением движения квантовой частицы. УстановленоЭрвином Шрёдингером в 1926 году.

13. Решение уравнения Шредингера для свободной микрочастицы и находящейся в потенциальной яме.

    Уравнение Шредингера. Стационарное уравнение Шредингера. Решение уравнения Шредингера для свободной частицы.

Уравнение Шредингера.

где: h = 1,05610 ³⁴ Дж·с - постоянная Планка, m - масса микрочастицы,

- оператор Лапласа, U - потенциальная энергия микрочастицы,

i - мнимая единица.

Стационарное состояние - это состояние микрочастицы со строго определенной энергией Е. Для стационарного состояния волновая функция имеет вид

где - волновая функция, зависящая только от координат.

Стационарное уравнение Шредингера.

Стационарное уравнение Шредингера для электрона в водородопо-добном ионе

где: Z - зарядовое число

(Z = 1 для водорода, Z = 2 для He⁺ , Z = 2 для Li⁺⁺), m = 9,11·10^–31 кг - масса электрона, е = 1,6·10^–19 Кл - заряд электрона, ε ₀ = 8,85·10 ¹² Ф/м - электрическая постоянная, h = 1,056·10-³⁴ Дж·с - постоянная Планка, r - расстояние от ядра до электрона, Е - энергия электрона,

- волновая функция, зависящая только от координат.

Т ак как поле, в котором движется электрон, является центрально-симметричным, то для решения данного уравнения обычно используют сферическую систему координат

В теории дифференциальных уравнений показано, что уравнение

и меет решения, удовлетворяющиетребованиям однозначности, конеч-ности и непрерывности волновой функции ψ, только при собственных значениях энергии

где n = 1, 2, 3, … - главноеквантовое число.

Таким образом, решение уравнения Шредингера для атома водоро-да (Z = 1) приводит к появлению дискретных энергетических уровней E₁, E₂, E₃, … , показанных на рисунке в виде горизонтальных прямых.

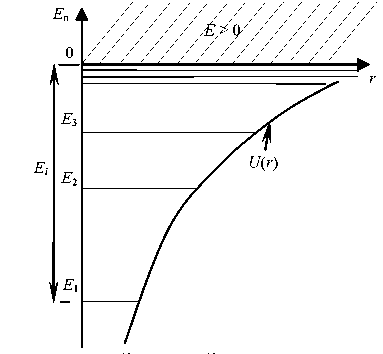
Состояниес наименьшей энергией является основным

все остальные состоянияназываются возбуждённые.

По мере роста главного квантового числа n энергетические уровни располагаются теснее и при n = ∞ энергия E_∞ = 0. При E > 0 движение электрона является свободным.

Энергия ионизации атома водорода

И з решения уравнения Шредингера вытекает, что момент импуль­са электрона не может быть произвольным, а принимает дискретные значения

где l - орбитальное квантовое число, которое при заданном n принима­ет значения l = 0, 1, 2, …, (n - 1), т.е. всего n значений.

Из решения уравнения Шредингера следует также, что вектор мо­мента импульса электрона может иметь лишь такие ориентации в про­странстве, при которых его проекция на направление oz внешнего маг­нитного поля принимает квантованные значения, кратные h

г де ml - магнитное орбитальноеквантовое число, которое при задан­ном l может принимать значения m_l = 0,±1,±2,...,± l., т.е. всего 2l + 1

значений.

Спин электрона - это собственный механический момент импуль­са электрона, не связанный с движением электрона в пространстве.

Спин электрона (и всех других микрочастиц) - квантовая величина, у неё нет классического аналога; это внутреннее неотъемлемое свойст­во электрона, подобное его заряду и массе.

Собственный механический момент импульса (спин) Ls согласно общим выводам квантовой механики квантуется по закону

где s =1\2 спиновое квантовое число.

Проекция спина на направление внешнего магнитного поля при­нимает квантованные значения,кратные h

г де m_s - магнитное спиновое квантовое число, которое имеет только два

значения

Хотя энергия электрона и зависит только от главного квантового числа n, но каждому собственному значению энергии E _n (кроме E ₁) со­ответствует несколько собственных функций отличаю­щихся значениями квантовых чисел l, ml и m_s Следовательно, атом во­дорода может иметь одно и тоже значение энергии, находясь в несколь­ких различных состояниях, соответствующих данному n.