
- •Внешний фотоэффект и его законы.
- •3. Дифференциальное уравнение незатухающих гармонических колебаний
- •Уравнение Эйнштейна для фотоэффекта
- •Пружинный маятник
- •Тепловое излучение, характеристики, закон планка.
- •Основные законы теплового излучения
- •Условия возникновения интерференции.
- •Интерференция от двух источников
- •Электрический колебательный контур. Энергия электромагнитных колебаний.
- •Сложение колебаний одного направления и одинаковой частоты.
- •Плоские, сферические, цилиндрические волны.
- •Сложение взаимно-перпендикулярных колебаний
- •Виды поляризации света
- •Дифференциальное уравнение затухающих электромагнитных колебаний
- •Метод зон Френеля. Дифракция Френеля.
- •Дифференциальное уравнение вынужденных колебаний
- •Дифракция Фраунгофера на одной щели.
- •Резонанс токов и напряжений
- •Волновые процессы, продольные и поперечные волны
- •Стоячие волны.
- •Естественный и поляризованный свет. Закон Малюса
- •Волновое уравнение электромагнитной волны
- •Дифракция Света. Принцип Гюйгенса-Френеля.
- •Вращение плоскости поляризации в оптически активных веществах
- •Скорость распространения электромагнитных волн. Свойства электромагнитных волн
- •Поляризация при отражении и преломлении
- •Электромагнитная природа света
- •Двойное лучепреломление
- •Интерференция световых волн. Условия максимумов и минимумов.
- •Дифракционная решетка.
- •Кольца ньютона в отраженном и проходящем свете
- •Когерентность и монохроматичность световых волн
- •Определение n максимума при дифракции Фраунгофера.
- •Получить из формулы планка закон Больцмана.
Интерференция от двух источников
Свет от одного источника с помощью непрозрачного экрана с двумя отверстиями даёт возможность получить два когерентных источника волн (схема Юнга). Расстояние между источниками (В, С) равно l. Длина волны, излучаемая источниками λ, расстояние до экрана, где наблюдается интерференция. О – центр экрана.
Пусть
в точке М – экрана происходит наложение
когерентных волн. Получим условие
усиления и ослабления волнами друг
друга. Расстояние от В источника до
точки М – d1, от С до точки М – d2. Колебания
точки М, вызываемые первым. источником
волн:
![]()
а
колебания, вызываемые 2-ым источником:
![]()
Результирующее
колебание точки М:
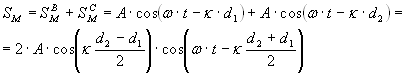
Амплитуда колебаний точки М:
AM=2Acos(k(d2-d1)/2) зависит от положения точки на экране и может быть равной 2А, если волны усиливают друг друга или нулю, если волны ослабляют друг друга.
Получим условие усиления или максимум интерференции. Чтобы АМ=2А, необходимо чтобы
|cos(k(d2-d1)/2)|=1
Это выполняется, если
![]()
Значит d2-d1=±mλ.
Пусть d2-d1=Δd – разность хода интерферирующих лучей, а ΔФ=2π(d2-d1)/λ=2πΔd/λ – разность фаз интерферирующих волн, тогда ΔΤ=2π/λ (d2-d1) =2π/λ Δd – ρоотношение между разность фаз и разность хода волн.
Если d2-d1=Δd=± mλ, γде m=0,1…, то АМ=2А и, следовательно, в этих точках пространства (экрана) наблюдается максимум интерференции. Разность фаз волн при этом будет равна ΔФ=±2πmλ/λ=±2πm.
Условие ослабления или минимум интерференции Ам=0, |cos(k(d2-d1)/2)|=0.
Это выполняется, если (k(d2-d1)/2)=±(2m+1)λ/2; следовательно Δd=±(2m+1)λ/2.
Волны ослабляют друг друга, если разность хода при этом ΔΤ=±2πmλ /(2λ)(2m+1)=±(2m+1)π,
m – называется порядком интерференционного максимума или минимума. В центре экрана наблюдается максимум нулевого порядка: d2-d1=Δd=0.
Электрический колебательный контур. Энергия электромагнитных колебаний.
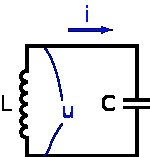
Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания
Резонансная
частота контура определяется так
называемой формулой Томсона:
![]()
Пусть конденсатор ёмкостью C заряжен до напряжения U0. Энергия, запасённая в конденсаторе составляет
![]() При
соединении конденсатора с катушкой
индуктивности, в цепи потечёт ток , что
вызовет в катушке электродвижущую силу
(ЭДС) самоиндукции, направленную на
уменьшение тока в цепи. Ток, вызванный
этой ЭДС (при отсутствии потерь в
индуктивности) в начальный момент будет
равен току разряда конденсатора, то
есть результирующий ток будет равен
нулю. Магнитная энергия катушки в этот
(начальный) момент равна нулю.
При
соединении конденсатора с катушкой
индуктивности, в цепи потечёт ток , что
вызовет в катушке электродвижущую силу
(ЭДС) самоиндукции, направленную на
уменьшение тока в цепи. Ток, вызванный
этой ЭДС (при отсутствии потерь в
индуктивности) в начальный момент будет
равен току разряда конденсатора, то
есть результирующий ток будет равен
нулю. Магнитная энергия катушки в этот
(начальный) момент равна нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора Ес =0. Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
![]() где
L
— индуктивность катушки, I0
— максимальное значение тока.
где
L
— индуктивность катушки, I0
— максимальное значение тока.
После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения U0.
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
При
этом вся энергия W колебательного контура
заключена в электрическом поле
конденсатора, т.е.
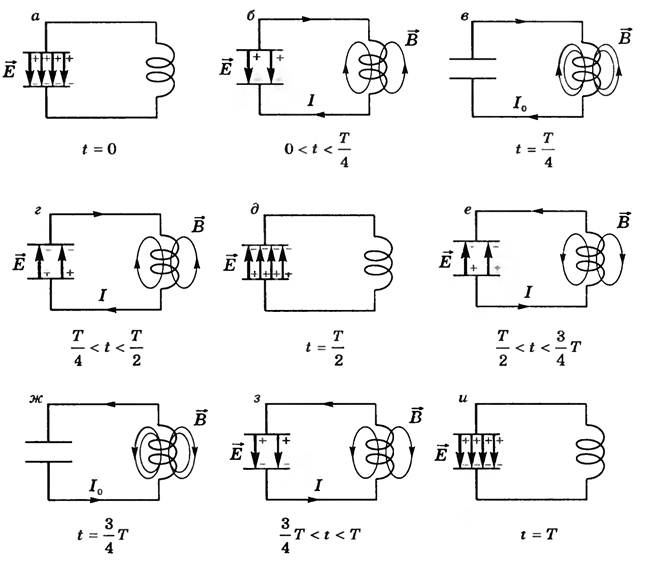
![]() В промежутке времени от 0 до Т/4(рис. 2,
б) конденсатор, разряжаясь, создает
через контур ток I, идущий по часовой
стрелке. При этом согласно правилу Ленца
в катушке возникает ЭДС самоиндукции,
препятствующая нарастанию этого тока.
К моменту времени Т/4 (рис. 2, в) конденсатор
полностью разряжается, напряжение U
между его обкладками становится равным
нулю, и электрическое поле в нем
отсутствует К этому времени ток 1 в
контуре и индукция В магнитного поля
этого тока достигают максимальных
значений. Следовательно, вся энергия
контура заключена в этот момент в его
магнитном поле, т.е.
В промежутке времени от 0 до Т/4(рис. 2,
б) конденсатор, разряжаясь, создает
через контур ток I, идущий по часовой
стрелке. При этом согласно правилу Ленца
в катушке возникает ЭДС самоиндукции,
препятствующая нарастанию этого тока.
К моменту времени Т/4 (рис. 2, в) конденсатор
полностью разряжается, напряжение U
между его обкладками становится равным
нулю, и электрическое поле в нем
отсутствует К этому времени ток 1 в
контуре и индукция В магнитного поля
этого тока достигают максимальных
значений. Следовательно, вся энергия
контура заключена в этот момент в его
магнитном поле, т.е.
![]()
В
промежутке времени от Т/4 до Т/2 при
уменьшении тока в катушке возникает
ЭДС самоиндукции и индукционный ток,
направление которого, согласно правилу
Ленца, совпадает с направлением убывающего
разрядного тока. К моменту времени Т/2
(рис. 2, д) ток в контуре прекращается,
следовательно, исчезает магнитное поле
Напряженность электрического поля Е
и напряжение U конденсатора максимальны.
Таким образом, вся энергия колебательного
контура заключена теперь в его
электрическом поле, т.е.
![]()
в промежутке времени от 1/2 Т до 3/4Т (рис. 2, е) конденсатор вновь разряжается и создает в контуре ток. Однако теперь положительно заряжена нижняя обкладка конденсатора, поэтому направление тока I в контуре меняется на противоположное. К моменту времени 3/4 Т(рис. 2, ж) конденсатор полностью разряжается, напряжение U между его обкладками падает до нуля, электрическое поле исчезает а ток I в контуре и индукция В магнитного поля в этот момент максимальны. Вся электрическая энергия контура превратилась в энергию магнитного поля, т.е.
В промежутке времени от 3/4Т до Т (рис. 14.2, з) сила тока уменьшается, а возникшая в катушке ЭДС самоиндукции препятствует этому. На верхней пластине появляются избыточные положительные заряды, а на нижней — отрицательные. К моменту времени Т (рис. 2, и) ток в контуре прекращается, исчезает магнитное поле, а напряженность Е электрического поля конденсатора и напряжение U между его обкладками максимальны. Значит, вся энергия колебательного контура заключена теперь в его электрическом поле, т.е.
вторая перезарядка возвращает контур в исходное состояние. Таким образом, завершилось полное колебание. В дальнейшем процесс повторяется в уже описанном порядке.
Характеристики затухающих ЭМ колебаний.
Скорость
затухания колебаний определяется
коэффициентом затухания ГАММА . В
соответствии с выражением (7.1.7) коэффициент
затухания обратен по величине тому
промежутку времени, за который амплитуда
колебаний уменьшается в «e»=2.718 раз.
Период затухающих колебаний определяется
формулой:
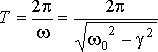
С
ростом ГАММА период увеличивается,
отсюда можно вычислить зависимость:
![]()
Такое
отношение амплитуд называется декрементом
затухания, а его натуральный логарифм
- логарифмическим декрементом затухания:
![]()
Помимо
рассмотренных величин для характеристики
колебательной системы употребляется
величина
![]() , называемая добротностью
колебательной системы. Добротность
пропорциональна числу колебаний,
совершаемых системой за то время, за
которое амплитуда колебаний уменьшается
в «e» раз. Большим значениям добротности
соответствует малое затухание.
, называемая добротностью
колебательной системы. Добротность
пропорциональна числу колебаний,
совершаемых системой за то время, за
которое амплитуда колебаний уменьшается
в «e» раз. Большим значениям добротности
соответствует малое затухание.
