
- •Внешний фотоэффект и его законы.
- •3. Дифференциальное уравнение незатухающих гармонических колебаний
- •Уравнение Эйнштейна для фотоэффекта
- •Пружинный маятник
- •Тепловое излучение, характеристики, закон планка.
- •Основные законы теплового излучения
- •Условия возникновения интерференции.
- •Интерференция от двух источников
- •Электрический колебательный контур. Энергия электромагнитных колебаний.
- •Сложение колебаний одного направления и одинаковой частоты.
- •Плоские, сферические, цилиндрические волны.
- •Сложение взаимно-перпендикулярных колебаний
- •Виды поляризации света
- •Дифференциальное уравнение затухающих электромагнитных колебаний
- •Метод зон Френеля. Дифракция Френеля.
- •Дифференциальное уравнение вынужденных колебаний
- •Дифракция Фраунгофера на одной щели.
- •Резонанс токов и напряжений
- •Волновые процессы, продольные и поперечные волны
- •Стоячие волны.
- •Естественный и поляризованный свет. Закон Малюса
- •Волновое уравнение электромагнитной волны
- •Дифракция Света. Принцип Гюйгенса-Френеля.
- •Вращение плоскости поляризации в оптически активных веществах
- •Скорость распространения электромагнитных волн. Свойства электромагнитных волн
- •Поляризация при отражении и преломлении
- •Электромагнитная природа света
- •Двойное лучепреломление
- •Интерференция световых волн. Условия максимумов и минимумов.
- •Дифракционная решетка.
- •Кольца ньютона в отраженном и проходящем свете
- •Когерентность и монохроматичность световых волн
- •Определение n максимума при дифракции Фраунгофера.
- •Получить из формулы планка закон Больцмана.
Вращение плоскости поляризации в оптически активных веществах
Естественное вращение. Некоторые вещества, называемые оптически активными, обладают способностью вызывать вращение плоскости поляризации проходящего через них плоскополяризованного света. К числу таких веществ принадлежат кристаллические тела (например, кварц, киноварь), чистые жидкости (скипидар, никотин) и растворы оптически активных веществ в неактивных растворителях (водные растворы сахара, винной кислоты и др.).
Кристаллические вещества сильнее всего вращают плоскость поляризации в случае, когда свет распространяется вдоль оптической оси кристалла. Угол поворота φ пропорционален пути l, пройденному лучом в кристалле: φ=αl.(15)
Коэффициент α называют постоянной вращения. Эта постоянная зависит от длины волны (дисперсия вращательной способности).
В растворах угол поворота плоскости поляризации пропорционален пути света в растворе l и концентрации активного вещества c: φ=[α]cl.(16) Здесь [α] – величина, называемая удельной постоянной вращения.
В зависимости от направления вращения плоскости поляризации оптически активные вещества подразделяются на право- и левовращающие. Направление вращения (относительно луча) не зависит от направления луча. Поэтому, если луч, прошедший через оптически активный кристалл вдоль оптической оси, отразить зеркалом и заставить пройти через кристалл еще раз в обратном направлении, то восстанавливается первоначальное положение плоскости поляризации.
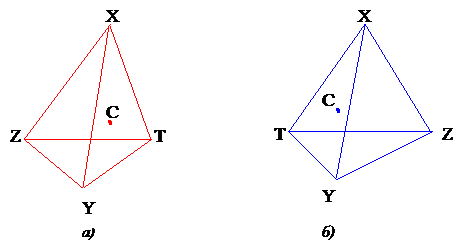
Все оптически активные вещества существуют в двух разновидностях – правовращающей и левовращающей. Существуют правовращающий и левовращающий кварц, право- и левовращающий сахар и т. д. Молекулы или кристаллы одной разновидности являются зеркальным отражением молекул или кристаллов другой разновидности (рис.6.12). Буквами C, X, Y, Z и T обозначены отличающиеся друг от друга атомы или группировки атомов (радикалы). Молекула б является зеркальным отражением молекулы а. Если смотреть на тетраэдр, изображенный на рис. 6.12, вдоль направления CX, то при обходе по часовой стрелке будет иметь место чередование ZYTZ для молекулы а и ZTYZ для молекулы б. То же самое наблюдается для любого из направлений CY, CZ, CT. Чередование радикалов X, Y, Z, T в молекуле б противоположно их чередованию в молекуле а. Поэтому, если, например, вещество, образованное молекулами а, правовращающее, то вещество, образованное молекулами б, будет левовращающим.
Скорость распространения электромагнитных волн. Свойства электромагнитных волн
Из теории Максвелла вытекает, что если в какой-либо малой области пространства периодически изменять электрическое и магнитное поля, то эти изменения должны периодически повторяться и во всех других точках пространства, причем в каждой последующей несколько позже, чем в предыдущей, т.е. от источника электромагнитных колебаний должны во все стороны распространяться электромагнитные волны с определенной скоростью. Вывод о конечности скорости распространения электромагнитных волн — очень важное следствие из теории Максвелла.
Дж.
Максвелл чисто математически показал,
что скорость распространения
электромагнитного поля в вакууме равна
3*10^8 м/с скорости света а в среде эта
скорость ν меньше и зависит от свойств
среды:
![]()
где ε — диэлектрическая проницаемость среды, μ — магнитная проницаемость среды.
Электромагнитная
волна, как и упругая, является носителем
энергии, причем перенос энергии
совершается в направлении распространения
волны. Энергию электромагнитной волны
можно рассчитать по формуле
![]()
где V — объем среды, в котором сосредоточена электромагнитная волна.
Вектор Пойнтинга и импульс электромагнитного поля.
В
силу симметричности тензора
энергии-импульса, все три компоненты
вектора пространственной плотности
импульса электромагнитного поля равны
соответствующим компонентам вектора
Пойнтинга, делённым на квадрат скорости
света:
![]() В
этом соотношении проявляется материальность
электромагнитного поля.
В
этом соотношении проявляется материальность
электромагнитного поля.
Поэтому, чтобы узнать импульс электромагнитного поля в той или иной области пространства, достаточно проинтегрировать вектор Пойнтинга по объёму.
