16 Динамическая модель механизма

Для механизмов с одной степенью подвижности удобно использовать одномассовую динамическую модель механизма (рис. 5.1).

При исследовании этой мо­дели принимают следующие допущения: все звенья считаются абсолютно твердыми, кинематические па­ры недеформируемыми. Зазоры в парах отсутствуют.

На рис. 5.1, а изображена кинематическая схема кривошипно-ползунного рычажного механизма с жесткими звеньями и одной степенью свободы. Движение всех звеньев такого меха­низма полностью определяется законом движения (φ, ω, ε) начального звена ОА, где φ – угол поворота; ω – угловая скорость, а ε – угловое ускорение начального звена.

Для отыскания этого закона движения с учетом сил F_C и M_C, действующих на механизм, используют одну из двух представленных на рис. 5.1 динами­ческих моделей.

а − кинематическая схема механизма; б и в – динамические модели механизма

На рис. 5.1, в модель, в которой масса всех звеньев заменяется приведенным моментом инерции I_пр диска, жестко связанного со звеном ОА. Силы, действующие на механизм в этом случае, заменяются приведенными моментами сил М_С ^пр и М_D ^пр . Приведенной силой (моментом) называют условную силу (момент), которая, будучи приложена к звену приведения, развивает мощность Р, равную мощности приводимых сил и моментов в рассматриваемом положении механизма.

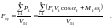
Приведенный момент силы равен

где F_k – величина приводимой силы, приложенной в точке k механизма;

V_к – скорость точки k; α_k – угол между векторами и . M_k – момент, приложенный к звену k; ω_k – угловая скорость k- го звена.

17 Приведенной массой m_пр называется такая условная масса, сосредоточенная в точке приведения, кинетическая энергия которой равна сумме кинетических энергий приводимых звеньев в данном положении механизма:

.

При приведении масс к вращающемуся звену (рис. 5.1,в) удобнее пользоваться понятием приведенного момента инерции I_np относительно оси вращения звена приведения:

,

где m_i , I_{S i} – масса и осевой момент инерции относительно оси, проходящей через центр масс i -го звена; V_{S i} , ω_i – соответственно скорость масс i -го звена и угловая скорость

i -го звена; V_A – скорость точки приведения; ω_ОА – угловая скорость звена приведения.

18 Истинная угловая скорость ω_1i, с^–1, и угловое ускорение ε_1i, с^–2, начального звена в i-м положении

; .

Здесь (y_ω.max – y_i) – расстояние по вертикали от верхней точки графика «ω – φ» до точки этого графика в i-м положении; – ордината диаграммы «(dω/dφ) – φ».

Время цикла установившегося движения машины, с:

t_ц = 60 ñ /n₁.

n₁ – частота вращения кривошипа, об/мин;

ñ – число оборотов начального звена за время одного цикла.

19 Для машин, в которых преобладает установившийся ре­жим движения, одним из критериев работоспособности является коэффициент δ неравномерности установившегося движения

δ = (ω_max − ω_min)/ ω_ср,

где ω_max, ω_min , ω_ср – соответственно максимальное, минимальное и среднее значения угловой скорости начального звена за цикл.

Определение момента инерции маховых масс машины

методом Мерцалова

Приведенный момент инерции J_м машины можно представить как сумму двух слагаемых J_м = J_c + J_v ,

где J_v – приведенный момент инерции звеньев механизма, связанных со звеном приведения переменным передаточным отношением;

J_c – приведенный момент инерции звеньев, связанных со звеном приведения постоянным передаточным отношением (маховых масс машины).

Кинетическую энергию машины представим как сумму

Т_м = Т_c + Т_v,

где Т_v ≈ ω_ср² J_v /2 ; ω_ср – средняя угловая скорость звена приведения при установившемся движении.

Экстремальные значения кинетической энергии маховых масс соответственно равны Т_c.max = ω _max ² J_c /2 ; Т_c.min = ω _min² J_c /2,

где ω _max и ω _min – максимальное и минимальное значение угловой скорости начального звена за цикл установивше­гося движения

ω _max = ω_ср (1+ [δ] /2); ω _min = ω_ср (1– [δ] /2),

где [δ] = (ω _max– ω _min) / ω_ср – допускаемый коэффициент неравномерности установившегося движения машины, заданный в исходных данных на проектирование.

Из совместного решения зависимостей четырех последних уравнений получим приведенный момент инерции маховых масс

J_c = (Т_c.max – Т_c.min) / ([δ] ω_ср²).