Частица в одномерной яме с абсолютно непроницаемыми стенками
Рассмотрим частицу в одномерной прямоугольной потенциальной яме с бесконечно высокими непроницаемыми стенками. Потенциальная энергия в этом случае удовлетворяет условиям
Поскольку частица может двигаться только вдоль оси х уравнение Шредингера для стационарных состояний примет вид
За пределами ямы
вероятность обнаружить частицу равна
нулю. Следовательно, и
.
Из условий непрерывности на границах
ямы
Для частицы в яме уравнение Шредингера имеет вид
.
Обозначим
.
Для уравнения
общим решением является
.
Так как
,
то B = 0 и
Условие
выполняется только при
,
где
(при
получается, что частица отсутствует).
Тогда
.
Выразив из
энергию, получим:
(7.9)
Спектр энергии
оказался дискретным. Квантованные
значения энергии
называются уровнями энергии, а число
n, определяющее
энергетические уровни частицы, главным
квантовым числом. Квантово-механическое
рассмотрение данной задачи приводит к
выводу, что частица в потенциальной яме
не может иметь энергию меньшую чем
при n = 1. Наличие
отличной от нуля минимальной энергии
не случайно и вытекает из соотношения
неопределенностей.
Если рассчитать
расстояние между соседними уровнями
энергии, в качестве частицы взяв электрон
г,
то для ямы шириной ~ 10 см (свободные
электроны в металле) получим
эВ.
То есть, чем больше m
и l, тем гуще располагаются
уровни энергии, так что спектр практически
можно считать непрерывным и квантование
энергии на характере движения частиц
сказываться не будет. Если же размеры
ямы соизмеримы с атомными l
~ 10-10м, то для электрона
эВ
и получаются явно дискретные значения
энергии. Этот результат является частным
случаем принципа соответствия Бора,
согласно которому законы квантовой
механики при больших значениях квантовых
чисел должны переходить в законы
классической физики.
Найдем собственные функции
Для нахождения А воспользуемся условием нормировки
В результате
интегрирования получим 
Откуда 
(
)
(7.10)
Графики собственных функций даны на рис.
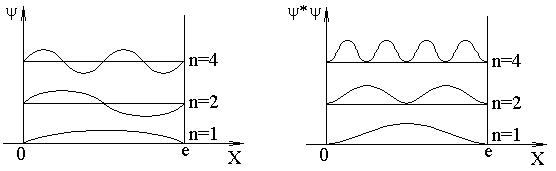
Из рис. следует, что, например, в квантовом состоянии n = 2 частица не может находиться в середине ямы, в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы, очевидно, несовместимо с представлением о траектории.
Пpохождение частицы чеpез одномеpный потенциальный баpьеp. Туннельный эффект
Различие в поведении
квантовых и классических частиц
проявляется в том случае, если на пути
частицы встречается потенциальный
барьер (при
,
при
)
П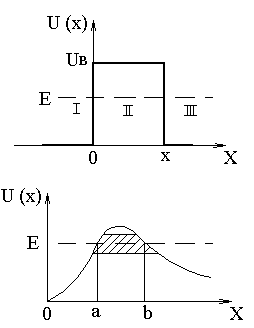
ри
данных условиях задачи классическая
частица, обладая Е (полная энергия
частицы), либо беспрепятственно пройдет
над барьером (при E
> U), либо отразится
от него (при E <
U) и будет двигаться
в обратную сторону. Для микрочастицы
же, даже при
,
имеется отличная от нуля вероятность,
что она отразится от барьера. При
имеется также отличная от нуля вероятность,
что частица окажется в области x
> l, т.е. проникнет
сквозь барьер. Подобные выводы следуют
из решения уравнения Шредингера для
стационарных состояний. Рассмотрим
случай
,
тогда для областей 1 и 3 имеем
для области 2
.
Общие решения этих дифференциальных уравнений:
(для области 1)
(для области 2)
(для области 3)
где
,
.
Решение вида
соответствует волне, распространяющейся
в положительном направлении оси х,
а решение вида
- волне, распространяющейся в противоположном
направлении. В области 3 имеется только
волна, прошедшая сквозь барьер и
распространяющаяся слева направо.
Поэтому коэффициент
следует принять равным нулю. Для
нахождения остальных коэффициентов
воспользуемся условиями, которым должна
удовлетворять функция .
Для того чтобы
была непрерывна во всей области изменений
х от - до + ,
должны выполняться условия:
и
.
Для того чтобы
была гладкой, т.е. не имела изломов,
должны выполняться условия:
и
.
Отношение квадратов модулей амплитуд отраженной и падающей волны
(7.11)
определяет вероятность отражения частицы от потенциального барьера и называется коэффициентом отражения.
Отношение квадратов модулей амплитуд прошедшей и падающей волны
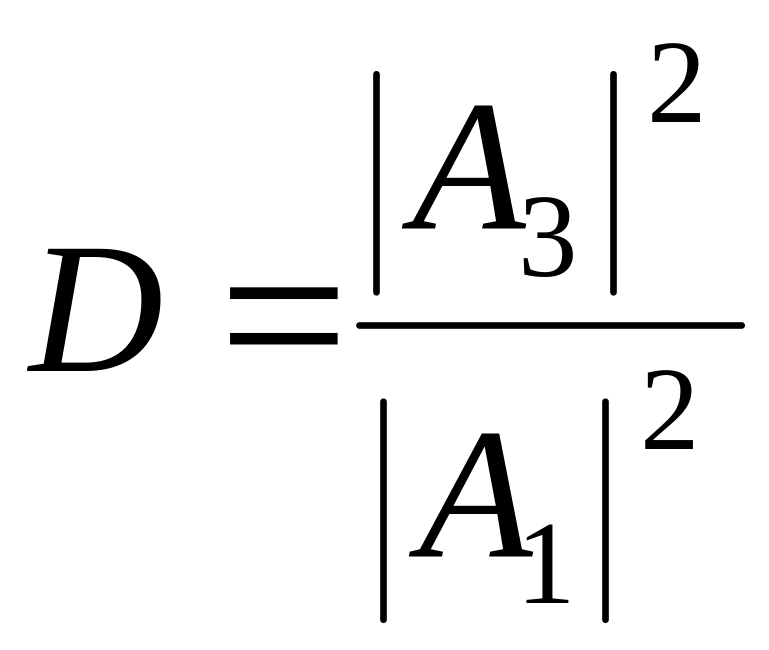
определяет вероятность прохождения частицы через барьер и называется коэффициентом прохождения (прозрачности). Для барьера конечной ширины
(7.12)
В случае барьера произвольной формы
При преодолении потенциального барьера частица как бы проходит через «туннель» в нем, в связи с чем данное явление называется туннельным эффектом. С классической точки зрения туннельный эффект представляется абсурдным, так как частица в туннеле должна была бы обладать отрицательной кинетической энергией . Однако туннельный эффект – явление специфически квантовое. В квантовой же механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит соотношению неопределенностей.
Поверхность металла
является потенциальным барьером, который
электроны преодолевают на глубину
и возвращаются обратно.