
- •1. Теория графов
- •1.1 Остовные деревья минимального веса.
- •Алгоритм Прим
- •Алгоритм Краскал
- •1.2 Нахождение кратчайших путей между двумя заданными вершинами. Алгоритм Дийкстры
- •Алгоритм Дийкстры
- •Модифицированный алгоритм Дийкстры
- •1.3 Нахождение кратчайших цепей между всеми парами узлов в сети
- •Алгоритм Флойда (Floyd r. W.)
- •Модификация алгоритма Флойда
- •1.4 Построение потоков максимальной мощности. Алгоритм Форда-Фалкерсона
- •Алгоритм Форда-Фалкерсона
- •1.5 Обобщенные задачи о потоке
- •1.5.1 Построение потока в сети с двойным ограничением потока по дугам
- •1.5.2 Построение потока в сети с пропускными способностями узлов
- •1.5.3 Построение потока в сети с несколькими источниками-стоками
- •1.5.4 Построение потока в сети с неориентированными ребрами
- •1.6 Определение потока заданной величины минимальной стоимости. Алгоритмы Басакера-Гоуэна, Клейна
- •Алгоритм Басакера-Гоуэна (Basaker r.G., Gowen p.J)
- •Алгоритм Клейна (Klein m.)
- •2 Сетевое планирование
- •2.1 Построение сетевых моделей
- •2.2 Расчет и анализ сетевых моделей
- •Задача №1
- •Задача №2
- •I. Поиск критических путей
- •II. Поиск резервов работ
- •Правило №2.1
- •3 Линейное программирование
- •3.1 Примеры задач лп
- •3.2 Свойства решений задач линейного программирования
- •3.3 Двумерные задачи линейного программирования. Графический метод решения. Исследование на разрешимость
- •3.3.1 Построение области допустимых решений целевой функции f.
- •3.3.2 Построение прямой уровня
- •3.3.3 Максимизация целевой функции f
- •3.4 Симплекс-метод.
- •3.4.1 Построение начального опорного плана.
- •3.4.2 Симплексные таблицы
- •3.4.3 Примеры решения задач симплекс-методом
- •4. Теория двойственности в линейном программировании
- •4.1 Понятие двойственности. Построение пары взаимно двойственных задач
- •4.2 Теоремы двойственности и их экономическое содержание
- •4.3 Анализ решения задач линейного программирования
- •5. Транспортная задача
- •5.1 Постановка транспортной задачи в матричной форме. Построение исходного опорного плана
- •5.2 Метод потенциалов
- •5.3 Дополнительные условия в транспортных задачах.
- •6. Дискретное программирование.
- •6.1 Метод Гомори для решения задачи целочисленного линейного программирования
- •7. Динамическое программирование
- •7.1 Многошаговые процессы в динамических задачах
- •7.2 Принцип оптимальности и рекуррентные соотношения
- •7.3 Вычислительная схема динамического программирования
- •7.4 Оптимальное распределение средств на расширение производства
- •8. Матричные игры
- •8.1 Парные матричные игры с нулевой суммой
- •8.2 Платежная матрица
- •Нижняя и верхняя цена игры
- •8.3 Смешанные стратегии
- •8.3 Решение матричной игры сведением к задаче линейного программирования
- •8.4 Решение матричной игры графическим методом
- •8.5 Приближенный метод решения матричных игр
- •Практические работы Практическая работа №1 Построение остовного дерева графа. Нахождение найкратчайшего расстояния между заданными вершинами графа
- •Практическая работа №2 Нахождение наикратчайших расстояний между всеми парами вершин графа. Алгоритм Флойда.
- •Практическая работа №3
- •Практическая работа №4 Нахождение потока заданной величины минимальной стоимости. Алгоритм Басакера-Гоуэна
- •Практическая работа №7 Оптимизация проекта по времени.
- •Практическая работа №8
- •Практическая работа №9 Оптимизация целевой функции с помощью двухфазного симплекс метода.
- •Практическая работа №10 Решение двойственных задач. Экономическая интерпретация задач линейного программирования.
- •Практическая работа №11 Решение транспортных задач.
- •Практическая работа №12 Дополнительные условия в транспортных задачах
- •Практическая работа №13 Метод Гомори для решения задачи целочисленного линейного программирования.
- •Практическая работа №14
- •Практическая работа №15 Решение матричных игр в чистых стратегиях
- •Практическая работа №16 Графический метод решения матричных игр.
- •Каркас минимального веса. Метод р. Прима.
- •Кратчайшие пути
- •Лабораторная работа №2 Кратчайшее расстояния от заданной вершины до всех остальных вершин графа.
- •Алгоритм Дийкстры.
- •Пути в бесконтурном графе.
- •Лабораторная работа №3 Кратчайшие пути между всеми парами вершин графа.
- •Алгоритм Флойда.
- •Лабораторная работа №4 Построение потока максимальной мощности.
- •Потоки в сетях.
- •Метод построения максимального потока в сети.
- •Лабораторная работа №5 Симплекс метод
- •Лабораторная работа №6 Транспортная задача
- •Список литературы
Практическая работа №7 Оптимизация проекта по времени.
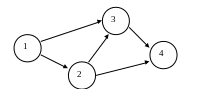
Проект представлен сетевым графиком (рис.). Продолжительность работ tij и минимальное время их выполнения dij, а также технологические коэффициенты использования дополнительных средств Аj приведены в табл.
Необходимо
определить величину дополнительных
вложений в каждую работу, при которых
время выполнения комплекса работ не
превышает t0,
а сумма дополнительных вложений
минимальна.
Номер варианта |
Параметры |
Работа (1,2) |
Работа (1,3) |
Работа (2,3) |
Работа (2,4) |
Работа (3,4) |
Срок выполнения |
1
|
tij |
10 |
20 |
15 |
10 |
25 |
35 |
dij |
7 |
10 |
9 |
5 |
14 |
||
kij |
0.05 |
0.3 |
0.4 |
0.1 |
0.2 |
||
2 |
tij |
10 |
20 |
0 |
10 |
25 |
30 |
dij |
7 |
10 |
0 |
5 |
14 |
||
kij |
0.05 |
0.3 |
0 |
0.1 |
0.2 |
Номер варианта |
Параметры |
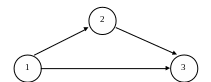
Работа (1,2) |
Работа (1,3) |
Работа (2,3) |
Срок выполнения |
3
|
tij |
7 |
5 |
4 |
8 |
dij |
4 |
2 |
3 |
||
kij |
0.3 |
0.4 |
0.7 |
||
4 |
tij |
10 |
20 |
8 |
11 |
dij |
6 |
7 |
2 |
||
kij |
0.1 |
0.2 |
0.3 |
||
5
|
tij |
14 |
25 |
10 |
21 |
dij |
12 |
7 |
8 |
||
kij |
0.1 |
0.4 |
0.2 |
||
6 |
tij |
15 |
17 |
9 |
20 |
dij |
10 |
14 |
5 |
||
kij |
0.1 |
0.7 |
0.4 |
||
7
|
tij |
11 |
15 |
19 |
23 |
dij |
4 |
6 |
12 |
||
kij |
0.2 |
0.3 |
0.1 |
Номер варианта |
Параметры |
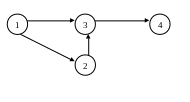
Работа (1,2) |
Работа (1,3) |
Работа (2,3) |
Работа (3,4) |
Срок выполнения |
8
|
tij |
20 |
10 |
0 |
7 |
190 |
dij |
11 |
6 |
0 |
4 |
||
kij |
0.1 |
0.8 |
0 |
0.4 |
||
9 |
tij |
11 |
17 |
0 |
9 |
210 |
dij |
5 |
8 |
0 |
4 |
||
kij |
0.07 |
0.02 |
0 |
0.05 |
||
10
|
tij |
9 |
12 |
0 |
17 |
210 |
dij |
4 |
8 |
0 |
5 |
||
kij |
0.08 |
0.1 |
0 |
0.06 |
