Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Минский государственный высший радиотехнический колледж

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

САиМ(методичка)_200811.doc

Скачиваний:

118

Добавлен:

27.09.2019

Размер:

5.97 Mб

Скачать

☆

<<< < Предыдущая 21 22 23 24 25 26 27 28 29 30 31 3233 / 4733 34 35 36 37 38 39 40 41 42 43 44 45 > Следующая >>>

Практическая работа №3

Построение потоков максимальной мощности. Алгоритм Форда-Фалкерсона.

Теоретическая часть:
Что называется сетью?
Определение «сток» и «исток» на сети.
Поток на сети.
Мощность потока на сети.
Пропускная способность дуг.
Разрез на сети.
Пропускная способность разреза.
Теорема Форда-Фалкерсона.
Прямая и обратная дуга.
Алгоритм Форда-Фалкерсона.
Алгоритм построения потока с двойным ограничением потока по дугам.
Алгоритм построения потока в сети с несколькими источниками-стоками.
Алгоритм построения потока в сети с неориентированными ребрами.
Алгоритм построения потоков в сети с пропускными способностями узлов.

Практическая часть:

В соответствии с вариантом для данной сети:

- определить максимальный поток на сети;

- построить разрез на сети;

- определить пропускную способность разреза

Вариант №1

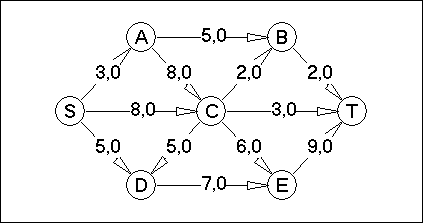
Вариант №2

Вариант №3

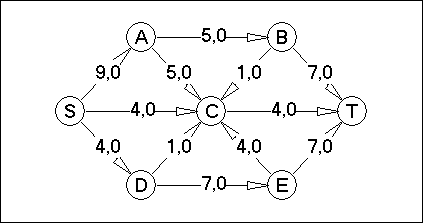
Вариант №4

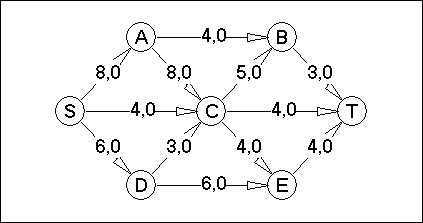
Вариант №5

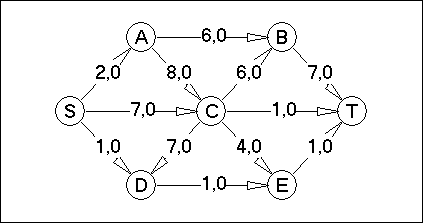
Вариант №6

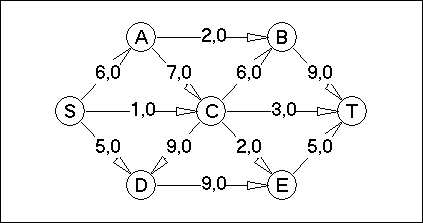
Вариант №7

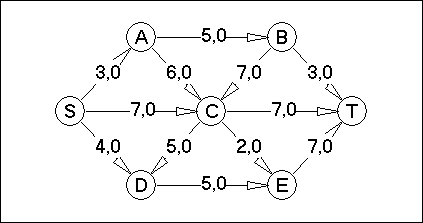
Вариант №8

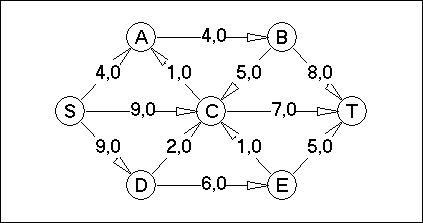
Вариант №9

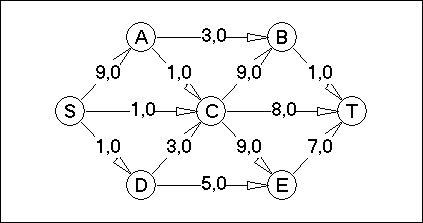
Вариант №10

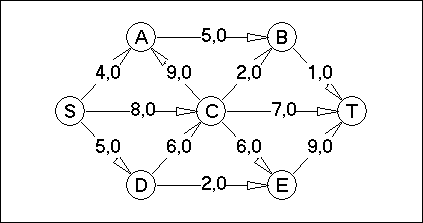
Вариант №11

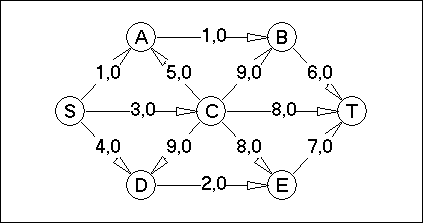
Вариант №12

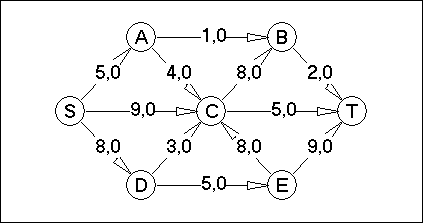
Вариант №13

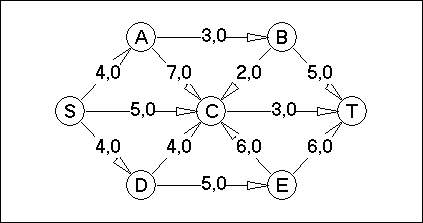
Вариант №14

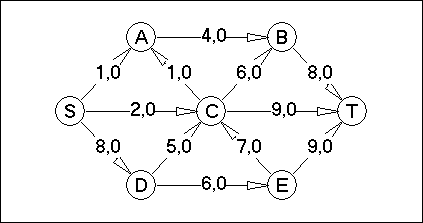
Вариант №15

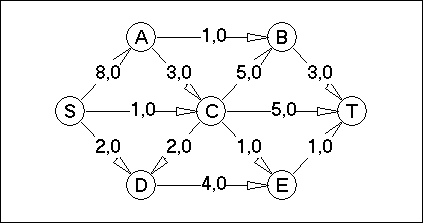
Вариант №16

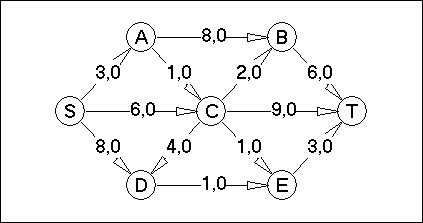
Вариант №17

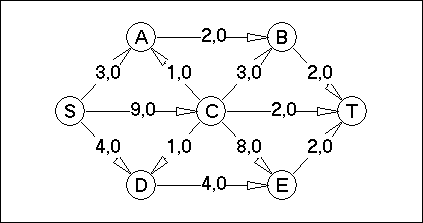
Вариант №18

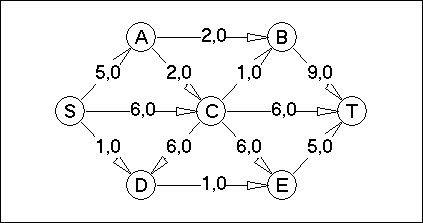
Вариант №19

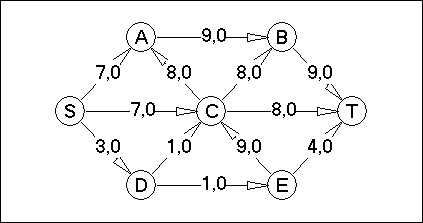
Вариант №20

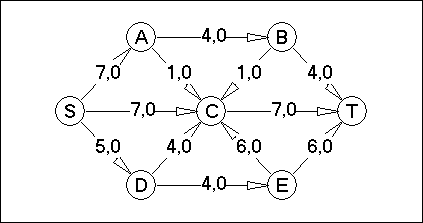
Вариант №21

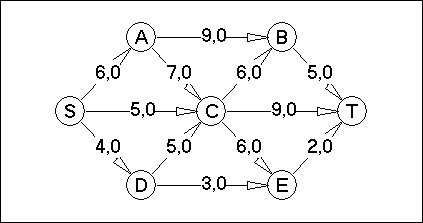
Вариант №22

Вариант №23

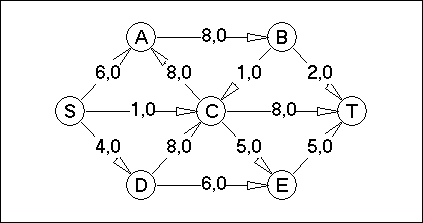
Вариант №24

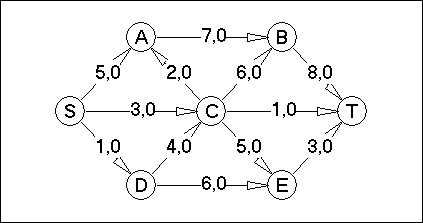
Вариант №25

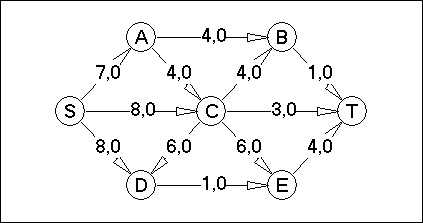
Вариант №26

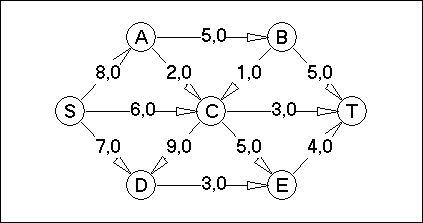
Вариант №27

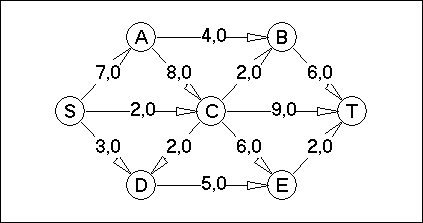
Вариант №28

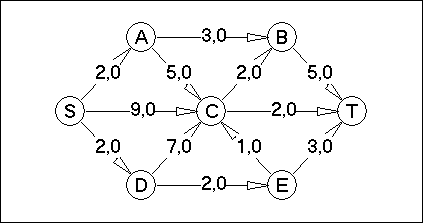
Вариант №29

Вариант №30

Практическая работа №4 Нахождение потока заданной величины минимальной стоимости. Алгоритм Басакера-Гоуэна

Теоретическая часть:

Стоимость доставки единицы потока по дуге?
Понятие графа модифицированных стоимостей?
Формулировка постановки задачи?
Нахождение потока заданной величины минимальной стоимости?
Алгоритм Басакера-Гоуэна?

Практическая часть:

Для сети (смотреть практическую работу №3) построить поток заданной мощности в соответствии с вариантом минимальной стоимости. На каждой дуге сети указаны два числа. Первое число означает пропускную способность ребра, а второе число указывает на поток по ребру. Стоимость доставки единицы потока по дуге указана в соответствии с вариантом.

Вариант №1

Вариант №2

Вариант №3

SA — 7

SC — 8

SD — 9

AB — 4

AC — 5

BC — 2

BT — 8

CD — 3

CE — 7

DE — 6

ET — 4

CT — 5

SA — 6

SC — 8

SD — 3

AB — 4

AC — 4

BC — 2

BT — 7

CD — 3

CE — 6

DE — 6

ET — 4

CT — 5

SA — 7

SC — 9

SD — 2

AB — 4

AC — 5

BC — 4

BT — 8

CD — 7

CE — 7

DE — 6

ET — 2

CT — 4

Вариант №4

Вариант №5

Вариант №6

SA — 2

SC — 6

SD — 9

AB — 5

AC — 6

BC — 7

BT — 8

CD — 3

CE — 7

DE — 4

ET — 4

CT — 3

SA — 6

SC — 3

SD — 4

AB — 4

AC — 5

BC — 2

BT — 5

CD — 3

CE — 7

DE — 6

ET — 7

CT — 9

SA — 4

SC — 8

SD — 2

AB — 4

AC — 5

BC — 9

BT — 8

CD — 7

CE — 7

DE — 2

ET — 4

CT — 5

Вариант №7

Вариант №8

Вариант №9

SA — 3

SC — 4

SD — 9

AB — 6

AC — 8

BC — 6

BT — 4

CD — 3

CE — 7

DE — 3

ET — 7

CT — 9

SA — 8

SC — 9

SD — 6

AB — 8

AC — 2

BC — 5

BT — 5

CD — 4

CE — 7

DE — 6

ET — 7

CT — 6

SA — 6

SC — 3

SD — 5

AB — 4

AC — 5

BC — 2

BT — 5

CD — 9

CE — 7

DE — 5

ET — 7

CT — 9

Вариант №10

Вариант №11

Вариант №12

SA — 7

SC — 5

SD — 9

AB — 5

AC — 3

BC — 7

BT — 8

CD — 9

CE — 7

DE — 8

ET — 4

CT — 3

SA — 3

SC — 6

SD — 9

AB — 6

AC — 6

BC — 8

BT — 8

CD — 6

CE — 7

DE — 2

ET — 4

CT — 5

SA — 2

SC — 7

SD — 7

AB — 9

AC — 3

BC — 5

BT — 7

CD — 3

CE — 4

DE — 4

ET — 7

CT — 8

Вариант №13

Вариант №14

Вариант №15

SA — 4

SC — 3

SD — 6

AB — 8

AC — 3

BC — 7

BT — 6

CD — 9

CE — 5

DE — 8

ET — 7

Вариант №16

SA — 5

SC — 5

SD — 6

AB — 5

AC — 7

BC — 7

BT — 8

CD — 8

CE — 7

DE — 8

ET — 4

Вариант №17

SA — 2

SC — 4

SD — 8

AB — 2

AC — 9

BC — 4

BT — 8

CD — 9

CE — 7

DE — 2

ET — 7

Вариант №18

SA — 7

SC — 4

SD — 8

AB — 5

AC — 3

BC — 7

BT — 2

CD — 9

CE — 7

DE — 8

ET — 4

CT — 6

SA — 6

SC — 3

SD — 9

AB — 4

AC — 8

BC — 6

BT — 8

CD — 9

CE — 7

DE — 7

ET — 6

CT — 3

SA — 5

SC — 5

SD — 7

AB — 6

AC — 7

BC — 7

BT — 9

CD — 5

CE — 9

DE — 8

ET — 4

CT — 2

Вариант №19

Вариант №20

Вариант №21

SA — 2

SC — 6

SD — 7

AB — 5

AC — 6

BC — 7

BT — 5

CD — 3

CE — 7

DE — 6

ET — 4

CT — 3

SA — 8

SC — 5

SD — 9

AB — 4

AC — 4

BC — 9

BT — 8

CD — 4

CE — 7

DE — 4

ET — 8

CT — 7

SA — 6

SC — 6

SD — 5

AB — 5

AC — 6

BC — 7

BT — 8

CD — 9

CE — 7

DE — 8

ET — 4

CT — 6

Вариант №22

Вариант №23

Вариант №24

SA — 4

SC — 4

SD — 7

AB — 2

AC — 9

BC — 8

BT — 8

CD — 9

CE — 7

DE — 7

ET — 7

SA — 2

SC — 8

SD — 8

AB — 2

AC — 4

BC — 4

BT — 6

CD — 9

CE — 7

DE — 2

ET — 9

SA — 6

SC — 2

SD — 7

AB — 2

AC — 9

BC — 4

BT — 8

CD — 7

CE — 7

DE — 2

ET — 7

Вариант №25

Вариант №26

Вариант №27

SA — 5

SC — 5

SD — 7

AB — 5

AC — 6

BC — 7

BT — 5

CD — 5

CE — 7

DE — 6

ET — 4

CT — 3

SA — 8

SC — 6

SD — 8

AB — 5

AC — 6

BC — 8

BT — 5

CD — 3

CE — 7

DE — 8

ET — 4

CT — 8

SA — 2

SC — 6

SD — 7

AB — 7

AC — 6

BC — 7

BT — 5

CD — 3

CE — 7

DE — 6

ET — 7

CT — 3

Вариант №28

Вариант №29

Вариант №30

SA — 4

SC — 5

SD — 4

AB — 5

AC — 6

BC — 4

BT — 5

CD — 4

CE — 7

DE — 9

ET — 4

CT — 3

SA — 9

SC — 5

SD — 7

AB — 9

AC — 6

BC — 7

BT — 9

CD — 5

CE — 7

DE — 9

ET — 4

CT — 3

SA — 3

SC — 5

SD — 7

AB — 5

AC — 3

BC — 7

BT — 5

CD — 3

CE — 7

DE — 8

ET — 4

CT — 9

Практическая работа №5

Нахождение потока заданной величины минимальной стоимости. Алгоритм Клейна.

Для сети построить поток заданной мощности минимальной стоимости, используя алгоритм Клейна. V=6

Вариант 1

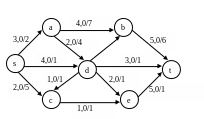
Вариант 2

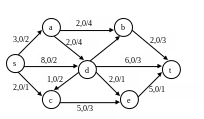
Вариант 3

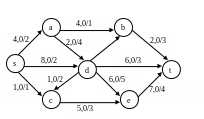
Вариант 4

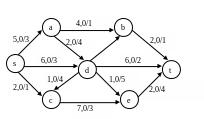
Вариант 5

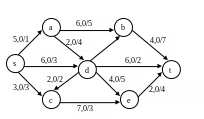
Вариант 6

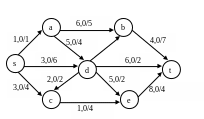
Вариант 7

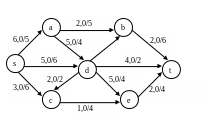
Вариант 8

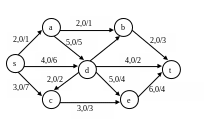
Вариант 9

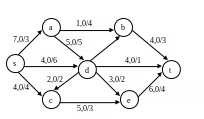
Вариант 10

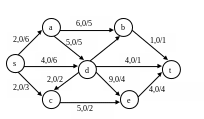
Практическая работа №6

Сетевое планирование.

Модели управления проектами.

Построить и рассчитать временные характеристики сетевых графиков.

Вариант 1

Проект разработки и внедрения нового вида продукции включает в себя следующие работы (табл.).

Таблица 1

Работа	Предшествующие работы	Продолжительность работы, мес.
А₁	-	1
А₂	-	5
А₃	А₁	3
А₄	А₁	2
А₅	А₂, А₃	6
А₆	А₂, А₃	5
А₇	А₄, А₅	5
А₈	А₆	3

Требуется:

построить сетевой график проекта;
рассчитать минимальное время выполнения проекта;
рассчитать временные параметры свершения событий;
определить сроки выполнения работ и их резервы времени;
построить линейный график выполнения работ проекта.

Вариант 2.

Фирма «Астра» запланировала реконструкцию своего офиса. Перечень работ, которые необходимо для этого выполнить, представлены в табл..

Таблица 2

Работа	Предшествующие работы	Продолжительность работы, мес.
А₁	-	5
А₂	А₁	10
А₃	А₁	5
А₄	А₂	3
А₅	А₂	5
А₆	А₄	3
А₇	А₃	4
А₈	А₇	5
А₉	А₅, А_6, А₈,	39

Требуется:

построить сетевой график проекта;
рассчитать минимальное время выполнения проекта;
рассчитать временные параметры свершения событий;
определить сроки выполнения работ и их резервы времени;
построить линейный график выполнения работ проекта.

Вариант 3

Подготовка и проведение экскурсионного тура требует выполнения следующих работ (табл.)

Таблица 3

Работа	Предшествующие работы	Продолжительность работы, мес.
А₁	-	6
А₂	-	8
А₃	-	2
А₄	А₁	3
А₅	А₁	4
А₆	А₃	6
А₇	А₃	3
А₈	А₂, А₅,А₆	4
А₉	А₂, А₅,А₆	4
А₁₀	А₄, А₈,	2
А₁₁	А₇	3

Требуется:

построить сетевой график проекта;
рассчитать временные параметры свершения событий, пользуясь четырехсекторной схемой. Выделить критические работы, указать критический срок выполнения проекта;
определить сроки выполнения работ и их резервы времени;
построить линейный график выполнения работ проекта.

Вариант 4

Комплекс работ по организации спортивно-оздоровительного мероприятия для детей туристской школы приведен в табл.

Таблица 4

Работа	Предшествующие работы	Продолжительность работы, мес.
А₁	-	4
А₂	-	6
А₃	А₁	2
А₄	А₁	6
А₅	А₂, А₃	3
А₆	А₂, А₃	3
А₇	А₄, А₅	5

Требуется:

построить сетевой график проекта;
рассчитать минимальное время выполнения проекта;
рассчитать временные параметры свершения событий;
определить сроки выполнения работ и их резервы времени.

Вариант 5

Осуществление проекта требует выполнения ряда работ, перечень которых задан в табл.

Таблица 5

Работа	Предшествующие работы	Продолжительность работы, мес.
А₁	-	5
А₂	-	3
А₃	А₁	7
А₄	А₁	6
А₅	А₂	7
А₆	А₄, А₅	3
А₇	А₄, А₅	10
А₈	А₃, А₆	8

Требуется:

построить сетевой график проекта;
определить:
1. сколько времени потребуется для завершения проекта;
2. можно ли отложить выполнение работы А₄ на без отсрочки завершения проекта в целом;
3. на сколько месяцев можно отложить выполнение работы А₃ без отсрочки завершения проекта в целом.

Вариант 6

Проект подготовки нового экскурсионного тура состоит из восьми работ (табл.)

Таблица 6

Работа	Предшествующие работы	Продолжительность работы, мес.
А₁	-	3
А₂	-	6
А₃	А₁	2
А₄	А₂, А₃	5
А₅	А₄	4
А₆	А₅	3
А₇	А₂, А₃	9
А₈	А₆, А₇	3

Требуется:

построить сетевой график проекта;
рассчитать минимальное время выполнения проекта;
рассчитать временные параметры свершения событий;
определить можно ли отложить выполнение работы А₃ на без отсрочки завершения проекта в целом;
определить, на сколько месяцев можно отложить выполнение работы А₆ без отсрочки завершения проекта в целом.

Вариант 7

Университет рассматривает предложение о строительстве новой турбазы. Работы которой следует выполнить перед началом строительства, представлены в табл.

Таблица 7

Работа	Предшествующие работы	Продолжительность работы, мес.
А₁	-	6
А₂	А₁	8
А₃	А₁	12
А₄	А₃	4
А₅	А₃	12
А₆	А₄, А₅	15
А₇	А₂, А₅	12
А₈	А₆, А₇	8

Требуется:

построить сетевой график проекта;
найти критический путь;
определить, реально ли начать работу по строительству здания турбазы через год после принятия решения о начале проекта;
определить сроки свершения события, , пользуясь четырехсекторной схемой;
определить сроки выполнения работ и их резервы времени.

Вариант 8

Проект подготовки нового экскурсионного тура состоит из восьми работ (табл.)

Таблица 8

Работа	Предшествующие работы	Продолжительность работы, мес.
А₁	-	1
А₂	-	5
А₃	А₁	4
А₄	А₁	3
А₅	А₂	6
А₆	А₄, А₅	5
А₇	А₄, А₅	6
А₈	А₃, А₆	4

Требуется:

построить сетевой график проекта;
рассчитать минимальное время выполнения проекта;
рассчитать временные параметры свершения событий;
определить можно ли отложить выполнение работы А₃ на без отсрочки завершения проекта в целом;
определить, на сколько месяцев можно отложить выполнение работы А₆ без отсрочки завершения проекта в целом.

Вариант 9

Проект разработки и внедрения нового вида продукции включает в себя следующие работы (табл.).

Работа	Предшествующие работы	Продолжительность работы, мес.
А₁	-	5
А₂	-	8
А₃	А₁	4
А₄	А₂, А₃	5
А₅	А₄	3
А₆	А₅	3
А₇	А₂, А₃	9
А₈	А₆, А₇	12

Требуется:

построить сетевой график проекта;
рассчитать минимальное время выполнения проекта;
рассчитать временные параметры свершения событий;
определить сроки выполнения работ и их резервы времени;
построить линейный график выполнения работ проекта.

Вариант 10

Подготовка и проведение экскурсионного тура требует выполнения следующих работ (табл.)

Работа	Предшествующие работы	Продолжительность работы, мес.
А₁	-	5
А₂	-	9
А₃	-	3
А₄	А₁	5
А₅	А₁	7
А₆	А₃	6
А₇	А₃	3
А₈	А₂, А₅,А₆	4
А₉	А₂, А₅,А₆	4
А₁₀	А₄, А₈,	2

Требуется:

построить сетевой график проекта;
определить:
1. сколько времени потребуется для завершения проекта;
2. можно ли отложить выполнение работы А₄ на без отсрочки завершения проекта в целом;
3. на сколько месяцев можно отложить выполнение работы А₃ без отсрочки завершения проекта в целом.

<<< < Предыдущая 21 22 23 24 25 26 27 28 29 30 31 3233 / 4733 34 35 36 37 38 39 40 41 42 43 44 45 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.12.2018208.38 Кб61Раздел 3 МП ЭВС.doc
#
06.12.2018683.01 Кб48Раздел 4 МП ЭВС.doc
#
01.03.202583.63 Кб0реферат по рэа.docx
#
25.02.2016604.6 Кб51РУЭиК Пример выполнения курсового проекта.pdf
#
25.02.2016959.89 Кб42РЭУиК КУРСОВОЕ ПРОЕКТИРОВАНИЕ.pdf
#
27.09.20195.97 Mб118САиМ(методичка)_200811.doc
#
25.02.20162.07 Mб25САПР_Работа1_4.pdf
#
25.02.20161.1 Mб8САПР_Работа5.pdf
#
14.08.201965.02 Кб6Свободные экономические зоны (лекция).doc
#
16.12.2018152.16 Кб17Синтез комбинационной схемы.docx
#
28.07.2019184.83 Кб4Смута.doc