8.3 Решение матричной игры сведением к задаче линейного программирования

Пусть игра задана платёжной матрицей .

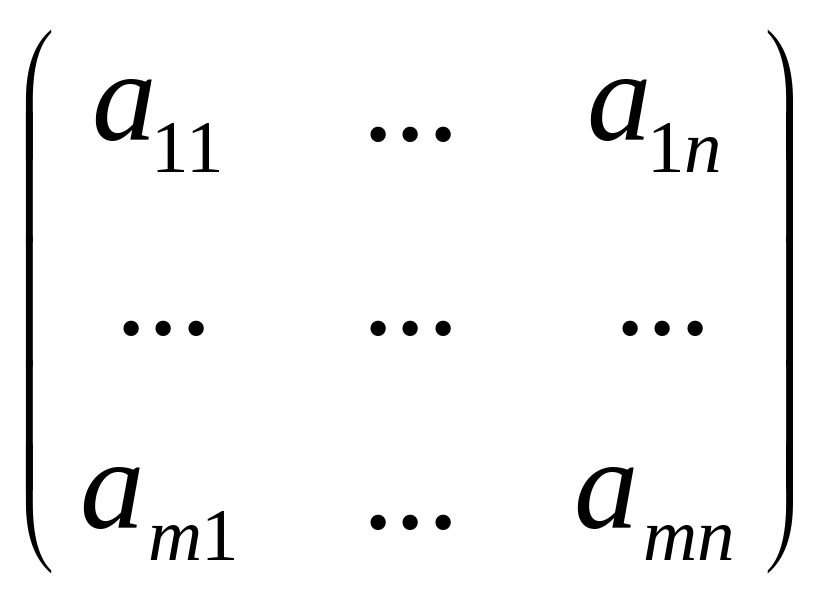Оптимальные смешанные стратегии и игроков А и В могут быть найдены в результате решения пары двойственных ЗЛП.

Для игрока А:

(j=1..n) (1.1)

(i=1..m)

В результате решения задачи (1.1) находят оптимальный вектор и , а затем

, (i=1..m) (1.2)

Для игрока В:

(i=1..m) (1.3)

(j=1..n)

Решая задачу (1.3), находят оптимальный вектор и ,

а затем

, (j=1..n) (1.4)

Поскольку задачи (1.1) и (1.3) образуют пару симметричных двойственных задач линейного программирования, нет необходимости решать обе задачи. Получив решение одной из них, достаточно воспользоваться соответствием между переменными последней симплекс-таблицы, содержащей компоненты оптимального вектора, выписать значения компонент оптимального вектора двойственной задачи.

Пример.

Решить игры с данными платёжными матрицами, сведя их к задачам линейного программирования.

1)

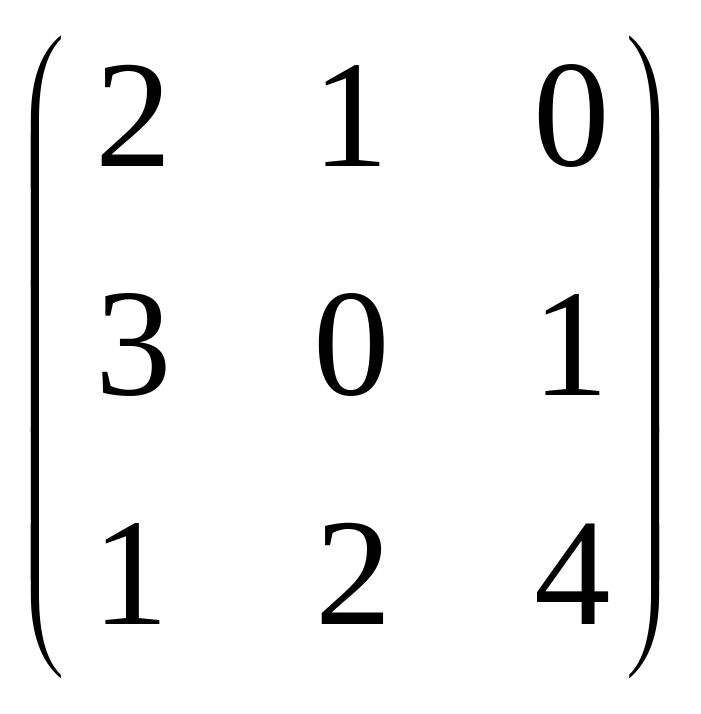
Проверим не имеет ли игра седловой точки. Находим

Т.к. , то решением игры будут смешанные стратегии, а цена игры заключена в пределах . По матрице игры составляем задачи (1.1) и (1.3)

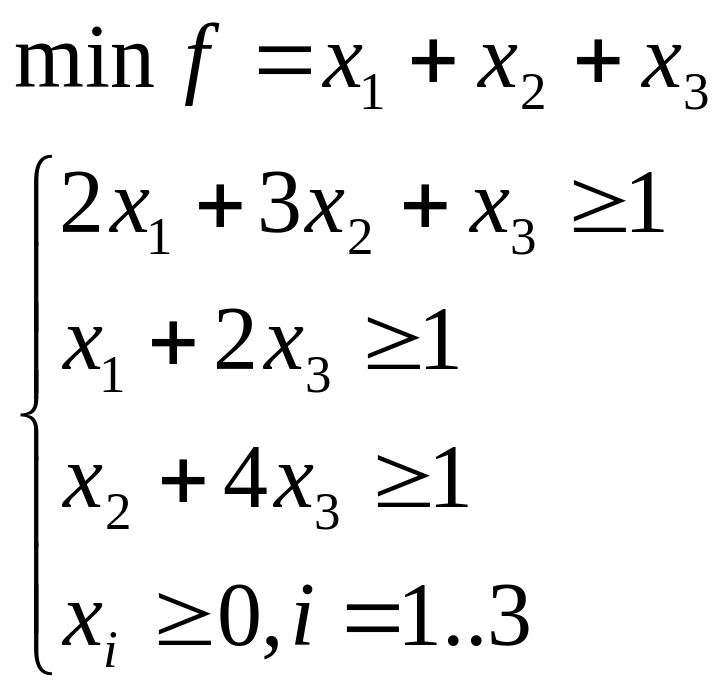(1.5)

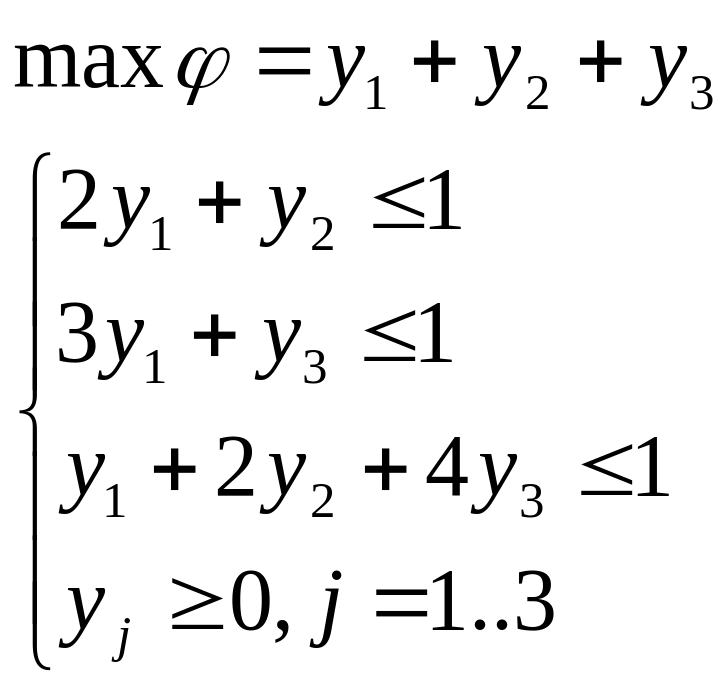(1.6)

Решим задачу (1.6), приводим к каноническому виду

-базисные, -свободные. Последняя симплексная таблица имеет вид:

Таблица 8.2

Б.п	Б.к
	1/3 1/3 0
	2/3	0	0	1/3	1/3	0	1/3

По формуле (1.4) получаем цену игры =3/2 и компоненты оптимальной смешанной стратегии игрока В.

Пользуясь соответствием переменных выпишем

Пользуясь формулами (1.2) находим компоненты оптимальной смешанной стратегии игрока А.

Решение игры: (1/2;0;1/2), =(1/2;1/2;0)

2)

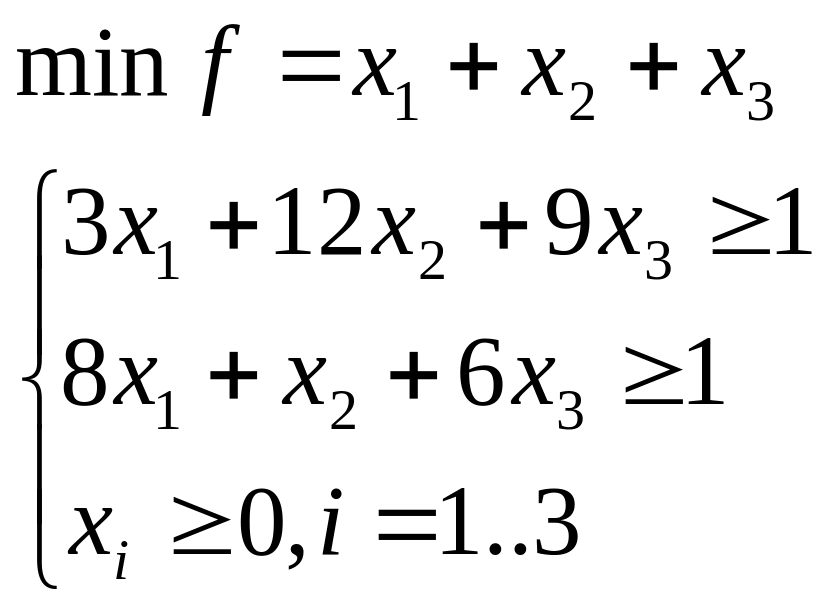
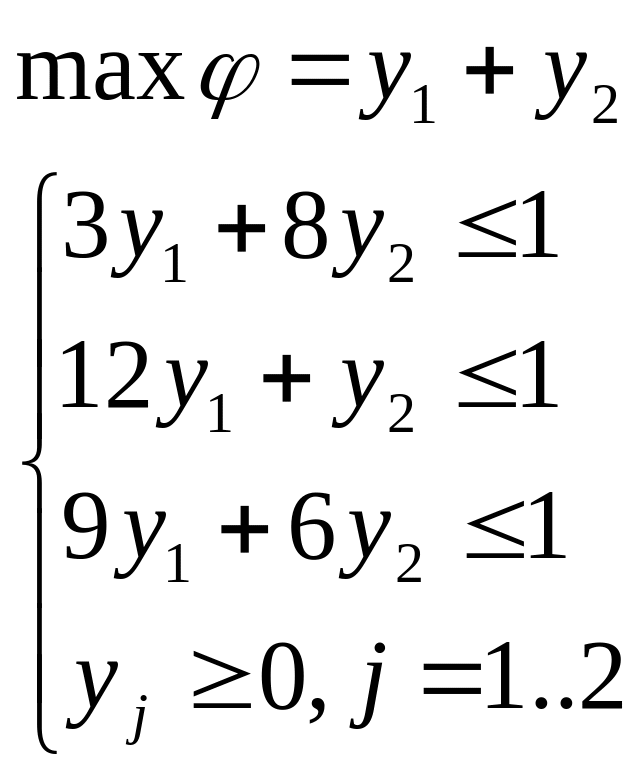
Используя формулы (1.4) получаем

Используя формулы (1.2), определяем , ,

(3/8;0;5/8)

=(1/4;3/4)

V=27/4

8.4 Решение матричной игры графическим методом

При поиске оптимальных стратегий в матричных играх размерностей 2 × n и m× 2 целесообразно использовать графический метод решения задач линейного программирования и свойства оптимальных планов пары двойственных задач: если в оптимальном плане задачи переменная положительна, то соответствующее ограничение двойственной задачи ее оптимальным планом обращается в равенство; если оптимальным планом задачи ограничение обращается в строгое неравенство, то в оптимальном плане двойственной задачи соответствующая переменная равна нулю.

Пример. Решить игру с платежной матрицей

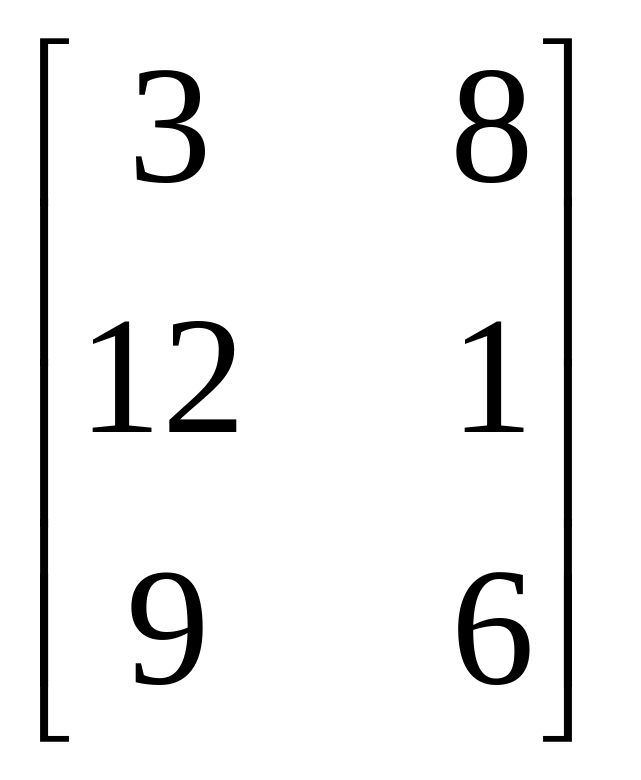графическим методом.

Решение В данном случае α = 6, β = 8, т.е. α ≠ β , а поэтому для определения оптимальных смешанных стратегий игроков составляем задачи

(1)

(2)

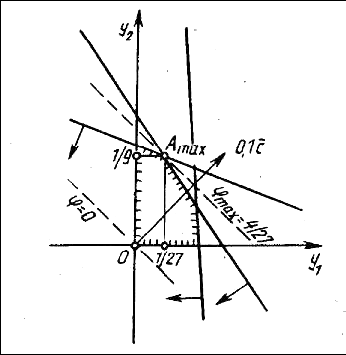
Поскольку одна из задач содержит две переменные, то, решим ее графически, находим: =1/27, =1/9, max = 4/27. Используя формулы v = 1/z_max; = v (j= ), получаем: v = 27/4, = 1/4, = 3/4.

Для определения оптимальной смешанной стратегии найдем сначала решение двойственной задачи. В оптимальном плане задачи (2) и ,поэтому оба ограничения двойственной задачи (1) ее оптимальным планом обращаются в равенства. Кроме того, значениями и второе ограничение задачи (2) обращается в строгое неравенство. Следовательно, в оптимальном плане задачи (1) соответствующая ему вторая переменная равна нулю, т. е. = 0. Учитывая сказанное, для определения и получаем уравнения 3х₁ + 9х₃ = 1 и 8 х₁ + 6 х₃ = 1, совместное решение которых дает =3/54, = 5/54.

Используя формулы v = 1/f_min; = v , определяем = 3/8, = 0, = 5/8. Итак, решение игры найдено:

= (3 / 8, 0, 5 / 8); = (1/ 4, 3 / 4); v = 27 / 4.

Пример.

Предприятие выпускает скоропортящуюся продукцию I и II. Данные о ее себестоимости, отпускных ценах и объемах реализации приведены в табл.8.3

На реализации. всей произведенной продукции расходуется 200 ден.ед. Определить ежедневный объем производства продукции по видам, обеспечивающий предприятию наибольший доход.

Таблица 8.3

Вид продукции	Себестоимость продукции, ден. ед.	Отпускная цена, ден.ед.		Объем реализации, ед.
		в день изготовления	позже	в теплую погоду	в холодную погоду
I II	0,8 0,5	1,2 0,8	0,3 0,2	1000 6000	4000 1200

Решение Используя игровой подход, примем за игрока А специалиста предприятия, принимающего решения об объемах выпуска продукции. Другим игроком будет природа, реализующая либо теплую (состояние П₁), либо холодную (состояние П₂) погоду. В предвидении той или иной погоды игрок А может дать указания о выпуске либо 1000 ед. продукции I и 6000 ед. продукции II (чистая стратегия А₁), либо 4000 ед. продукции I и 1200 ед. продукции II (чистая стратегия А₂). Т.о., описанная в задаче ситуация формализуется в игру с природой размерности 22 (табл.8.4)

Выигрышем a_ij игрока А будет величина дохода, получаемого предприятием в той или иной ситуации (А_i;П_j) (i,j=1,2).Доход от единицы продукции I составляет (1,2-0,8)ден.ед., если она реализуется в день изготовления, и (0,3-0,8) ден.ед. при более поздней реализации; доход от реализации продукции II — соответственно (0,8-0,5) и (0,2-0,5) ден.ед. Процедура реализации готовой продукции в каждой ситуации обходится предприятию в 200 ден.ед., при этом объем реализации определяется уровнем спроса, а спрос — погодой.

Таблица 8.4

Ai\Пj	П1(1000;6000)	П2(4000;1200)	pi
А1(1000;6000) А2(4000;1200)	2000 -940	-880 1760	p1 p2

Вычислим элементы a_ij платежной матрицы. Выигрыш a₁₁ игрока А соответствует комбинации (А₁;П₁). Это наиболее удачное для игрока А стечение обстоятельств: вся произведенная продукция будет реализована в день изготовления и суммарный доход с учетом затрат на продажу составит a₁₁ = (1,2-0,8)  1000+(0,8-0,5)  6000-200=2000 ден.ед.

Благоприятной будет и ситуация (А₂;П₂): a₂₂ = (1,2-0,8)  4000+(0,8-0,5)  1200-200=1760 ден. ед.

Сложнее обстоит дело в ситуации (А₁;П₂): если продукция I будет полностью реализована в день изготовления с доходов в (1,2-0,8)  1000 ден. ед (ее можно было бы продать и больше: спрос в 4000 ед, а изготовили только 1000 ед.!), то продукции II в день изготовления будет продано только 1200 ед. и доход от того составит (0,8-0,5)  1200 ден. ед., а остаток в 600-1200=4800 ед. придется реализовать позже с доходом в (0,2-0,5)  4800 ден. ед., так что суммарный доход а₁₂=(1,2-0,8)  1000+(0,8-0,5)  1200+(0,2-0,5)  4800-200 = -880 ден. ед.

Аналогичная обстановка сложится и в ситуации (А₂;П₁). Здесь доход а₂₁=(1,2-0,8)  1000 +(0,8-0,5) 1200 +(0,3-0,8)  3000-200=-940 ден. ед. Расчет элементов платежной матрицы закончен.

Приступая к решению игры, находим  = -880,  = 1760. Поскольку   , игру следует решать в смешанных стратегиях, причем только для сознательного игрока А, потому как природа П наши рекомендации не воспримет. Прежде чем составлять задачу линейного программирования, преобразуем элементы платежной матрицы по формуле а^’_ij=( а_ij + 940)/60. Тогда цена игры с преобразованной матрицей

выразится равенством v = (v + 940)/60, а модель задачи линейного программирования примет вид

Эта задача содержит две переменные, а поэтому, решив ее графически находим Определяем а затем находим цену

Оптимальные вероятности и применения игроком А своих чистых стратегий удобнее использовать на практике так: в среднем ежедневно целесообразно производить 1000 +4000 =2548 ед. продукции I и 6000 +1200 =3522 ед. продукции II. Тогда независимо от состояния погоды ежедневный наибольший доход предприятия будет составлять 482,2 ден.ед.