3.4.3 Примеры решения задач симплекс-методом

Пример 1. (задача об оптимальном распределении материалов). Имеющийся фонд материалов нужно так распределить между изготовителями, чтобы получить максимальную прибыль от реализации всей продукции, произведенной из данных материалов. Нормы расхода на единицу продукции и прибыль с_j, получаемая от реализованной единицы продукции, представлены в табл.

Таблица 4.3

Материал	Продукция					Объем материала
	П1	П2	П3	П4	П5
b1 b1 b1	0.7 1.4 0.5	0.9 0.3 2.1	1.5 0.7 1.8	2.3 2.5 0.7	1.8 2.0 2.0	50000 28000 40000
Прибыль сj	5	7	6	9	8
План х	х1	х2	х3	х4	х5

Решение Математическая модель задачи

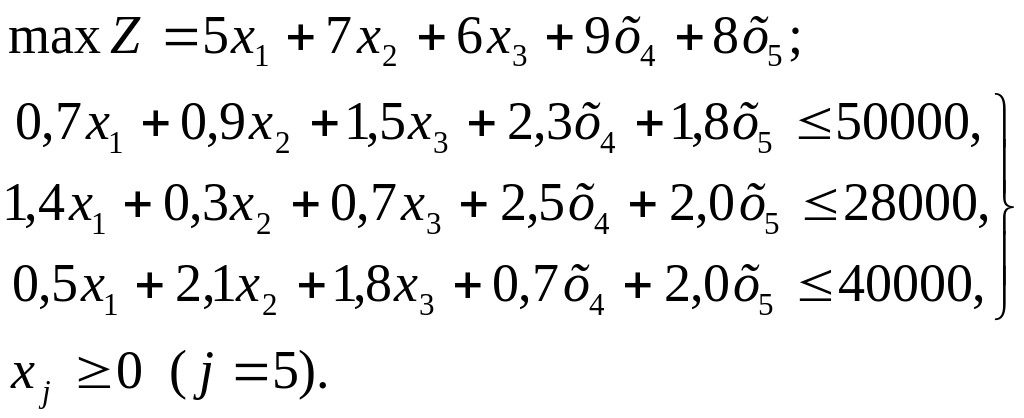
Введя дополнительные переменные х_6, х₇ и х₈, получим ее каноническую форму:

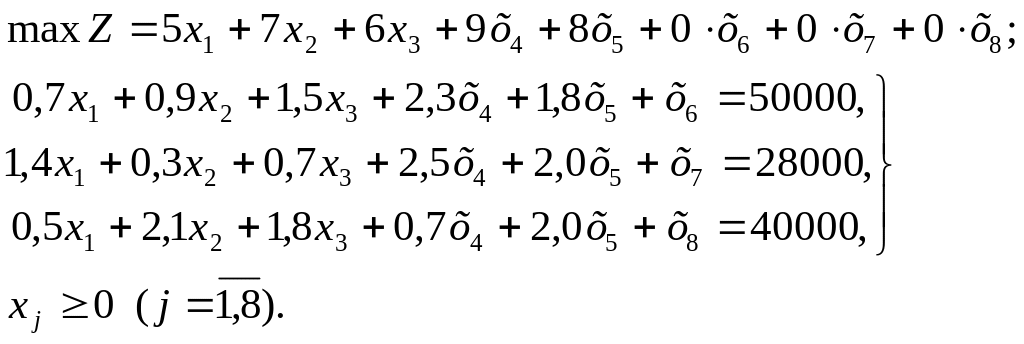
По индексной строке видно, что начальный опорный план неоптимален. Так как дополнительные переменные в канонической форме составляют допустимый единичный базис, то условия задачи заносим в симплексную таблицу.

Таблица 4.4

БП	сБ	А0	х1	х2	x3	х4	x5	x6	x7	x8
			5	7	6	9	8	0	0	0
х6	0	50000	0,7	0,9	1,5	2,3	1,8	1	0	0
х7	0	28000	1,4	0,3	0,7	2 ,5	2,0	0	1	0
x8	0	40000	0,5	2,1	1,8	0,7	2,0	0	01
zj-cj		0	-5	-7	-6	-9	-8	0	0	0
х6	0	24240	-0,59	0,62	0,86	0	-0,04	1	-0,92	0
х4	9	11200	0,56	0,12	0,28	1	0,8	0	0,4	0
x8	0	32160	0,11	2 ,02	1,6	0	1,44	0	-0,28	1
zj-cj		100800	0,04	-5,92	-3,48	0	-0,8	0	3,6	0
х6	0	14286	-0,62	0	0,36	0	-0,49	1	-0,83	-0,31
х4	9	9286	0,55	0	0,19	1	0,71	0	0,42	-0,06
x2	7	159525	0,05	1	0,8	0	0,72	0	-0,14	0,5
zj-cj		195238	0,36	0	1,23	0	3,43	0	2,78	2,94

Разрешающие элементы выбираем по описанным выше правилам. Все вычисления выполняются согласно правилам симплексных преобразований.

На втором шаге преобразований получаем оптимальный план – все оценки положительны.

Итак, х₀ = (0; 15 952; 0; 9286; 0; 14 286; 0; 0), т. е. имеющиеся материалы нужно распределить на выпуск продукции П₂ в объеме х^*₂ = 15 952 ед. и П₄ в объеме х^*₄ = 9286 ед. Реализация этой продукции даст 195 238 ден. ед.

На выпуск 15 952 ед. продукции П₂ нужно выделить: первого материала 0,9  15 952 = 14 356,8 ед., второго материала 0,3 15 952 = 4785 ед., третьего материала 2,1  15 952 = 33 499,1 ед.

На выпуск 9286 ед. продукции П₄ нужно выделить: первого материала 2,3  9286 = 21 357,8 ед., второго материала 2,5  9286 = 23 215 ед., третьего материала 0,7  9286 = 6500,2 ед.

Дополнительные переменные в оптимальном плане показывают объем неиспользуемых материалов: первого материала остается 14 286,4 ед., второй и третий материалы используются полностью.

Пример 2. Используя искусственный базис, решить ЗЛП

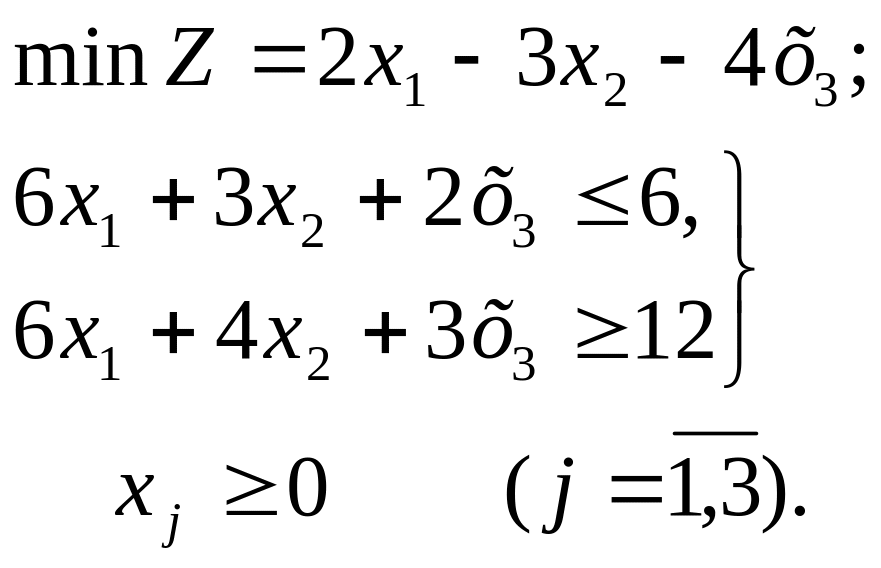
Решение Составляем соответствующую М – задачу и решаем ее обычным способом. После второй итерации все оценки(см. табл.) неположительны: _j  0 ( ). Следовательно, по признаку оптимальности опорный план (0; 0; 3; 0; 0; 3) оптимален. Но так как в оптимальном плане искусственная переменная w не равна нулю, то система ограничений исходной задачи несовместна. Задача решения не имеет.

Таблица 4.5

Номер итерации	БП	сБ	А0	х1	х2	x3	х4	x5	w
				2	-3	-4	0	0	М
2	х1	-4	3	3	3/2	1	1/2	0	0
	w	М	3	-3	-1/2	0	-3/2	-1	1
zj-cj			12+ 3М	-14 -3М	-3 -1/2М	0	-2 -3/2 М	- М	0