4.5. Алгоритм улучшения плана

Сформулируем теперь алгоритм перехода к новому опорному плану, дающему меньшее значение функции потерь. Прежде, чем формулировать его в общем виде, покажем его основные моменты на том примере, который мы начали рассматривать.

Вспомним, что ограничения двойственной задачи соответствовали тому, что , а выполнение условия говорило о том, что соответствующий вектор надо вводить в базис. Поэтому и выполнение

условия

говорит о том, что вектор

надо вводить в базис.

У нас условие выполнено в двух случаях  для и . Вообще

принято вводить в базис тот вектор, для которого

максимально. В данном случае это вектор ,

но в учебных целях мы

введем в базис вектор .

Введение в базис вектора означает, что мы должны запланировать какую-то перевозку из третьего склада в первый пункт потребления. Пусть величина этой перевозки равна  . Поставим ее в клетку, соответствующую i =3, j =1. Тогда мы получим следующий план перевозок:

2	3.1
	3.9	4.2
		2.8	6.3

Но теперь у нас нарушился баланс запасов и потребностей  получилось, что

из третьего склада вывозится ,

а в первый пункт потребления

поступает .

Необходимо восстановить баланс запасов и потребностей. Для этого поступают следующим образом: по ненулевым компонентам плана перевозок (включая и компоненту  ) строят цикл вида столбец  строка столбец строка ... строка (см. рисунок), который начинается и кончается на компоненте  .

Теперь для восстановления баланса запасов и потребностей можно поступить очень просто: при движении по столбцу от имеющихся компонентов плана надо отнимать  , а при движении по строке  наоборот, прибавлять  . В результате получится следующий план перевозок, уже сохраняющий баланс запасов и потребностей:

2-	3.1+
	3.9-	4.2+
		2.8-	6.3

С балансом всё в порядке, но теперь у нас стало компонент плана, а должно быть . Поэтому надо выбрать  так, чтобы одна из бывших компонент обратилась в нуль, но все остальные компоненты остались положительными. Легко догадаться, что для этого  надо взять равным минимальному из тех чисел, из которых  вычитается. В нашем случае  вычитается из чисел 2; 3.9; 2.8 . Минимальное из них есть 2 и поэтому надо взять  =2.

В результате получится новый опорный план следующего вида

	5.1
	1.9	6.2
2		0.8	6.3

в котором снова будет положенные ему

компонент.

Вычисляя транспортные расходы для этого плана, мы получим , откуда видно, что по сравнению с исходным планом транспортные расходы уменьшились на 2 единицы.

Опишем этот процесс в общем виде.

Итак, пусть для некоторой пары индексов выполнено условие . Тогда вектор надо вводить в базис. Если таких векторов окажется несколько, то обычно вводят в базис тот вектор, для которого

величина разности

максимальна.

Исходя из клетки строят цикл по ненулевым компонентам плана перевозок по маршруту столбец  строка  столбец  строка  ...  строка, который начинается и заканчивается в клетке . Мы не будем доказывать следующие два утверждения:

 такой цикл всегда может быть построен;

 такой цикл единственный.

Итак, пусть этот цикл имеет вид

Установим новый план перевозок вида

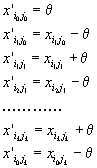
Все остальные компоненты плана перевозок, не входящие в цикл, остаются неизменными.

Наконец, выберем  таким образом, чтобы одна из новых компонент плана обратилась в нуль, а все остальные остались положительными. Для этого  следует взять в виде ,

где считается .

В результате получится новый опорный план. Покажем, что этот новый опорный план дает меньшее значение транспортных расходов, чем старый план.

Так как компоненты плана, не входящие в цикл, не изменяются, то их можно не учитывать. Для ненулевых компонент исходного плана

выполнялось условие

и поэтому

Для нового плана перевозок мы имеем

В выражении, стоящем в квадратных скобках, большинство слагаемых сокращается и окончательно получаем

так как мы вводим перевозку, для которой .

Ну, а дальнейшее очевидно: надо повторять все итерации до тех пор, пока не будет получен оптимальный план. В силу конечности числа вершин допустимой области, это может быть сделано за конечное число шагов.

Закончим наш учебный пример. Одну итерацию мы уже проделали.