1. Граф-схема решения задачи линейного программирования

Первая модель решения: на полном двудольном графе отношений.

Задача имеет очевидное решение, вытекающее из метода минимума транспортных расходов. Решение представлено на рис. 1.1.

Принято по дуге графа (А, 1) при С_А1=2 транспортировать 200 тонн и платить 2*200=400 усл. ед. стоимости.

Остаток бетона 320–200=120 отправляется на строку 2 при затратах на транспортировку 4*120=480 усл. ед. На стройку 3 по 6 усл. ед. за тонну его отправлять не выгодно.

А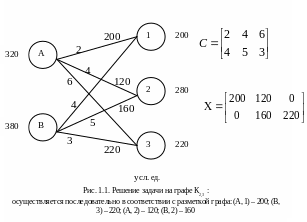 налогично имеем дугу (В, 3) с минимальными затратами 3*220=660 усл. ед. Остаток по дуге (В, 2) с неизбежными затратами 5*160=800 усл. ед.

Общая стоимость суточных затрат составит 2340 усл. ед. из единственности приведенного решения вытекает и его оптимальность.

Очевидность подобного утверждения можно показать с помощью спора моделей.

В данном случае под спором моделей понимается получение одинакового результата из разных моделей (методов) решения задач.

Для этого вместо топологии решения на графе сведем решение задачи к топологии метрического пространства с метрикой по Евклиду.

Другими словами, построим модели алгебраического вида и дадим их интерпретацию в двухмерном евклидовом пространстве.

1.2. Алгебраическая модель решения

задачи линейного программирования

Вторая модель. Алгебраический уровень описания задачи.

В общем случае задачи размерности 2х3, где и –обозначение мощности множества, т. е. числа элементов в множествах, имеет вид:

Дано:

Найти:

.

Однако не все переменные множества X является независимыми.

Табл. 1.1 позволяет облегчить поиск зависимых переменных с помощью системы уравнений. Для случая x₁=x₁₁ и x₂=x₁₂ имеем:

x₁₃ = x₃ = 320 – (x₁ + x₂)0

x₂₁ = x₄ = 200 – x₁0

x₂₂ = x₅ = 280 – x₂0

x₂₃ = x₆ = 220 – x₃ = x₁ + x₂ – 1000

x₁0 и x₂0.

Подстановка системы уравнений-ограничений (знак  0) в w дает:

.

Таблица 1.1

Для поиска зависимых переменных

	1	2	3	ai
A	x11	X12	x13	320
B	x21	x22	x23	380
bj	200	280	220	700

В итоге получена следующая задача линейного программирования в неравенствах

x10; x20 320– x1– x20 200– x10 280– x20 x1+x2–1000	x3=f3(x1;x2) x4=f4(x1) x5=f5(x2) x6=f6(x1;x2)
	w=fw(x1;x2)

Заметим, что, в отличие от графа К_2,3, алгебраическая модель совсем не напоминает задачу о бетоне, для решения которой была построена.

1.3. Геометрическая форма представления

процесса решения

Третья модель. Геометрическое решение задачи.

В случае двух независимых переменных поиск точки решения, соответствующей W_min , нагляднее произвести методами алгебраической геометрии в топологии Евклида.

С этой целью воспользуемся декартовой системой координат (x₁;x₂).

На рис. 1.2 приведена область допустимых решений, определенная неравенствами уравнений – ограничений.

Построена опорная прямая w’, параллельная искомой прямой w_min, т.е. w’ || w_min.

Определено направление перемещения опорной прямой w’ в сторону минимизации значений w.

Выделена точка x^опт=x⁰(200,120), соответствующая w_min.

Определено значение w_min(x⁰)=2340 усл. ед. Решение, полученное на модели 3, совпадает с решением, полученным на модели 1. Для наглядности на рис. 1.3. представлена линейная поверхность отклика (плоскость в 3-мерном пространстве) над линейной областью допустимых решений (область ОДЛР).