Вопросы 4+6k

4 . Пружинный маятник как гармонический осциллятор. Дифференциальные уравнения. Собственные колебания и энергия осциллятора.

Динамический метод.

- дифференциальное уравнение гармонического осциллятора.

, т.е. .

Решением дифференциального уравнения будет .

Энергетический метод.

Энергия с течением времени не меняется.

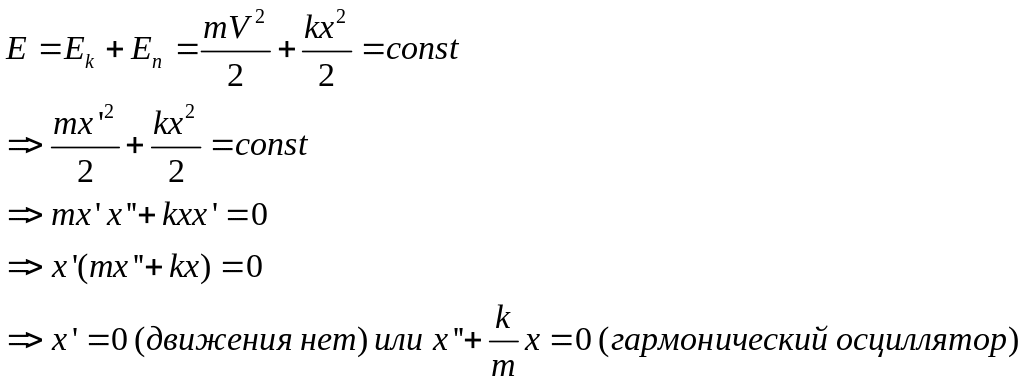
Система будет являться гармоническим осциллятором, если ее полная энергия является квадратичной функцией смещения и скорости.

Чтобы восстановить решение уравнения необходимо знать свойства системы и ее начальное состояние.

Причин колебаний 2:

1. возвращающая сила.

2. инертность.

3 свойства осциллятора:

1. Начальное положение.

2. Возвращающая сила.

3. Инертность.

10. Вынужденные колебания колебательного контура. Дифференциальное уравнение и его решение. Частота, амплитуда и фаза вынужденных колебаний. Явление резонанса.

Любая система может совершать вынужденные колебания за счет вынуждающего воздействия. Любое внешнее воздействие можно представить как сумму гармонических.

Колебательным системам свойственно явление резонанса. Колебательные системы, или осцилляторы, избирательно реагируют на частоту внешнего воздействия. Если эта частота совпадает с собственной частотой, то наблюдается явление резонанса (резкого возрастания амплитуды колебаний).

Д иф.ур. вынужденных колебаний колебательного контура.

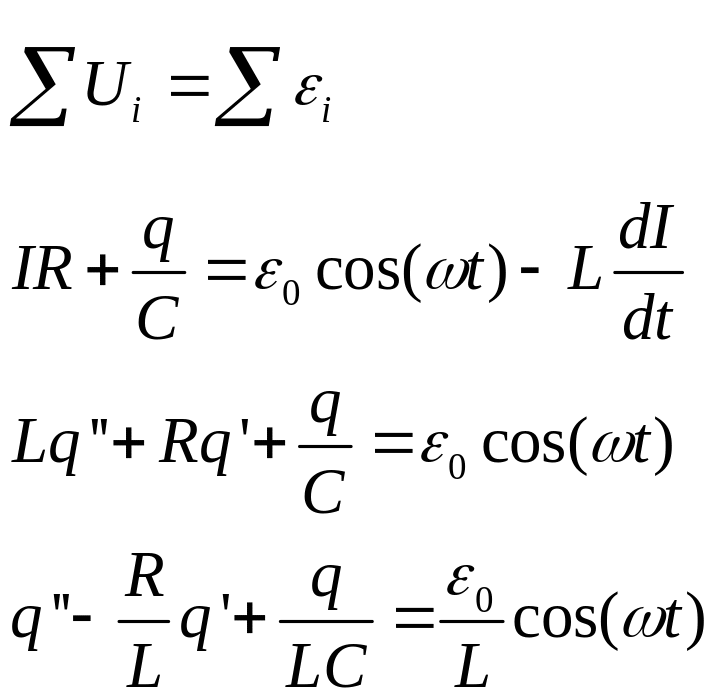
Здесь и далее идет описание в общем виде для пружинного маятника. Должно быть одно и тоже, с учетом следующих обозначений:

Решение.

_{В общем случае дифференциальное уравнение вынужденных колебаний:}

_{Дифференциальное уравнение вынужденных колебаний неоднородно. Справа не ноль. Общее решение неоднородного уравнения складывается из двух, а именно: решения общего однородного уравнения и частного решения неоднородного уравнения.}

_{Нас интересует частного решения неоднородного уравнения, которое определяет установившееся решение.}

_{Справа гармоническая функция, слева сумма трех функций, которые тоже должны быть гармоническими с той же частотой.}

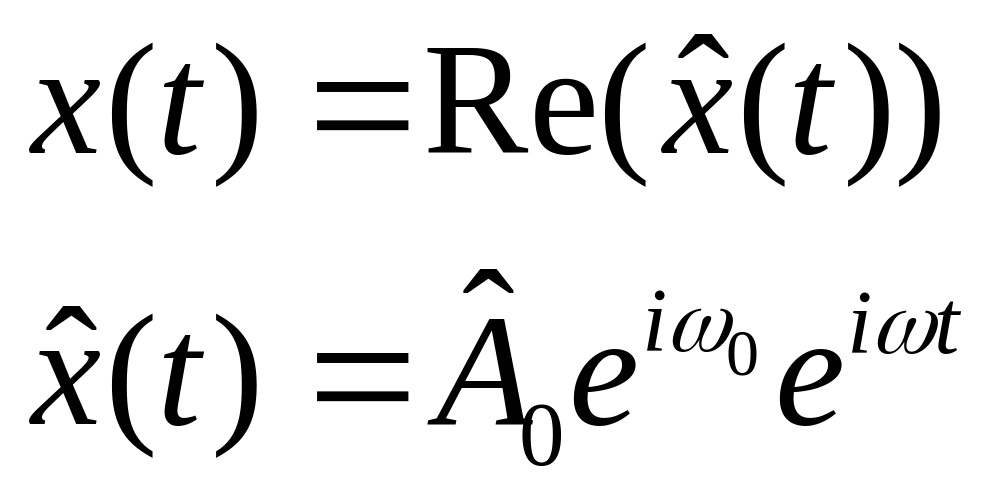
_{Осуществим подстановку:}

_{Ao= ; . Частное решение уравнения имеет вид:}

_{x(t)= cos(wt+ )}

_{Вынужденные колебания в системе оказались сдвинутыми по фазе по отношению к вынужденному воздействию.}

_{х=Acos(wt+o)}

_{1) Частота колебаний равна частоте вынужденных колебаний}

_{2) A(w) – амплитуда зависит от частоты воздействия. При разных частотах А(w) будет разной.}

_{3) о – разность фаз этого колебания и колебания вынужденного воздействия.}

_{Амплитуда вынужденных колебаний.}

_{При малых частотах; w << wо.}

_{(на примере маятника)}

_{При низкой частоте реакция на внешнее воздействие зависит от упругих свойств системы и от возвращающего воздействия. - статическое смещение}

1. _{При высоких частотах; w >> wо.}

_{При высоких частотах определяющим является инертность системы. Чем больше инертность, тем амплитуда колебаний меньше.}

2. _{При w = wо – резонанс.}

_{У зависимости А(w) должен быть максимум. Амплитуда максимальна, когда минимальна.}

_{wо, , fo – const, мы их зафиксировали.}

_w1=0

_{w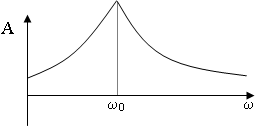 2= - резонансная частота.}

_{Когда частота воздействия равна резонансной частоте, тогда будет максимум амплитуды.}

_{=0, при выполнении этого условия явление резонанса исчезает. Если трение велико, то резонанса не будет.}

_{Резонанс скорости}

_{х=Acos(wt+jo)}

_v=

_vA=

_{1) низкие частоты.}

_{, т.е. движения нет.}

₂₎

_{Между w и vA должен быть максимум, следовательно резонанс скорости должен быть при любом значении трения.}

_{V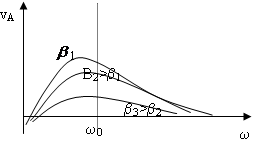 A=}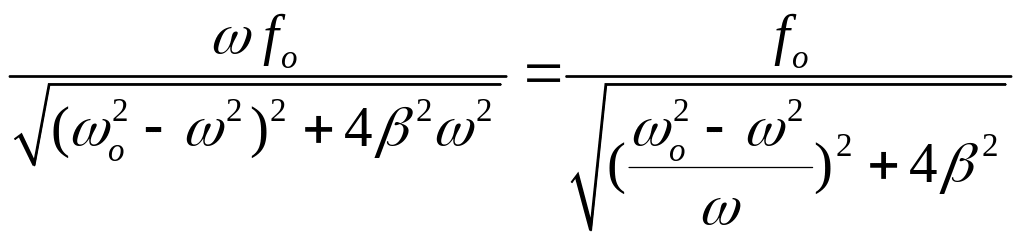

_{Скорость будет максимальной, когда частота вынужденного воздействия равна собственной частоте.}

_{Резонанс скорости существует всегда при любом трении.}

_{О т резонанса скорости в принципе нельзя избавиться, также существует резонанс ускорения.}

_{В условиях малого можно считать, что все частоты приблизительно равны 0.}

_{Фаза вынужденных колебаний.}

_{F = F0cos(t), x = Acos(t+}

1. _{=0, 0=0}

2. _{При произвольной частоте 0<0, т.е. колебания которые установятся в этой системе будут отставать по фазе от колебания воздействия.}

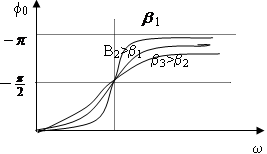_{ =  - характерная точка. В этом случае max одной системы приходится на 0 в другой и наоборот. F = F0cos(t), x = Acos(t - /2)}

_{Добротность и резонансные свойства системы}

_{Резонансные свойства системы можно характеризовать добротностью.}

_{Арез – резонансная частота}

_{Аст – статическое смещение}

_{1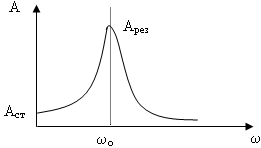 ) Аст , когда w = 0; Аст=}

_{2) Арез, когда w= wо; Арез=}

_{; - ширина кривой}

_{- добротность характеризует меру ширины резонансной кривой.}