13. Плоские гармонические волны и их характеристики. Фазовая и групповая скорости волн. Волновое уравнение.

Плоские гармонические волны и их характеристики.

Фронт волны – плоскость, перпендикулярная направлению распространения волны.

Пусть колебания листа происходят по закону косинуса. Смещение от положения равновесия .

Вызовем плоскость, которая соответствует волновому фронту, на расстоянии х от листа.

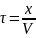
– время запаздывания колебаний, - скорость распространения волны.

Пусть потери энергии нет  амплитуда и частота будут точно такие.

где 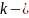волновое число и .

– уравнение плоской волны, где радиус вектор в любой точке волновой поверхности, – волновой вектор.

, где

• – фаза зависит от и .

• смещение

• амплитуда

• циклическая частота . Показывает быстроту изменения фазы колебаний в определенной точке пространства.

• частота

• –период

• волновое число . Показывает быстроту изменения фазы колебаний в пространстве в фиксированный момент времени.

• скорость волнового процесса. фазовая скорость волны.

• длина волны.

аналог , пространственный период волнового процесса.

Уравнение волны можно представить в комплексном виде: .

В общем случае , тогда .

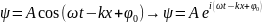Фазовая и групповая скорости волн:

Фазовая скорость – скорость распространения в пространстве постоянного значения фазы (определенного состояния).

Волновая поверхность – поверхность, на которой фаза волнового процесса одна и та же.

В случае плоских гармон. волн, волновые поверхности – это плоскости, расположенные параллельно. Частным случаем является волновой фронт.

Фазовая скорость зависит от типа волн и от среды. Может также зависеть от частоты. В этом случае принято говорить, что наблюдается дисперсия волн.

В реальности сущ. волновые процессы, ограниченные в пространстве и времени.

Произвольный волновой процесс можно представить в виде совокупности гармонических волн.

Рассмотрим волновой пакет, кот. предствл. из себя суперпозицию 2^х гармонических волн.

С такой скоростью распространяется энергия волны.

Волновое уравнение:

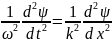
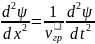
Если система описывается таким уравнением, то это означает, что с ней могут распространяться волны, а именно гармонические волны и их комбинации.

Общий вид волнового уравнения

19. Энергия электромагнитной волны. Вектор Пойнтинга. (но лучше взять с лекций)

Если знаем направление вектора E и вектора H, то мы знаем направление распространения волны.

25. Интерференция света на тонких пленках. Полосы равного наклона и равной толщины.

Закон преломления:

В месте отражения волн поделилась амплитуда

Эффективная разность хода складывается из 2^х величин. Учитывается потеря половины волны.

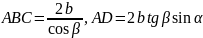
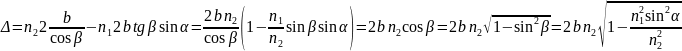
1. Полосы равного наклона

2. Полосы равной толщины

Если есть дефекты