ФИЗИКА

1. Гармонические колебания. Характеристики и формы представления.

Гармоническими колебаниями называются колебания, при которых колеблющаяся физическая величина изменяется по закону синуса (или косинуса).

Различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) могут быть представлены в виде суммы (суперпозиции) гармонических колебаний.

Гармоническое колебание величины описывается уравнением типа

где: амплитуда колебания – максимальное значение колеблющейся величины;

круговая (циклическая) частота;

начальная фаза колебания в момент времени ;

фаза колебания в момент времени .

Фаза колебания определяет значение колеблющейся величины в данный момент. Так как косинус изменяется в пределах от до , то может принимать значения от до .

Поскольку , то при гармонических колебаниях увеличение (приращение) фазы колебания на приводит к тому, что все величины, характеризующие колебание, принимает исходное значение.

Периодом колебаний называется наименьший промежуток времени, по истечении которого повторяются состояния колеблющейся системы (совершается одно полное колебание) и фаза колебания получает приращение

откуда

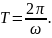
Частотой колебаний называется величина, обратная периоду колебаний – число полных колебаний, совершаемых в единицу времени

Единица частоты – герц (Гц) – частота периодического процесса, при котором за 1 секунду совершается один цикл колебаний.

Формы представления:

1. Аналитическая

2. Графическая

3. Векторная

,

.

4

4. Комплексная

где – комплексная амплитуда колебаний.

7. З атухающие колебания пружинного маятника. Дифференциальное уравнение и его решение. Характеристики колебаний. Энергия колебаний. Добротность.

Пружинный маятник – это груз массой , подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы

где – жесткость пружины.

Если на маятник действует сила трения, пропорциональная скорости , где – коэффициент сопротивления, то колебания маятника будут затухающими, и закон движения маятника будет иметь вид

или

В общем виде уравнение имеет вид

Решение будем искать в виде , которое подставим в уравнение и получим характеристическое уравнение:

откуда

Решение распадается на три случая:

• При малом трении ( ) общее решение записывается в виде: , где   — частота свободных колебаний.

• Затухание   называют критическим. Начиная с такого значения показателя затухания, осциллятор будет совершать так называемое неколебательное движение. В граничном случае движение происходит по закону: .

• При сильном же трении   решение выглядит следующим образом: , где  . Это апериодический режим.

Итак, имеем

Выражение можно интерпретировать как гармоническое колебание с частотой , у которого амплитуда с течением времени уменьшается по экспоненциальному закону.

Характеристики затухания:

1. – коэффициент затухания (определяет скорость падения амплитуды)

2. – время релаксации (постоянная времени затухания) – время, за которое амплитуда уменьшается в раз.

3. – декремент затухания – характеризует падение амплитуды – во сколько раз амплитуда меняется за один период.

4. – логарифмический декремент – величина, обратная числу колебаний, за которое амплитуда уменьшается раз.

Энергия колебаний.

1. 

нет трения

2. 

Добротность.

Добротность осциллятора численно равна приращению фазы, в течении которой энергия уменьшается в раз.