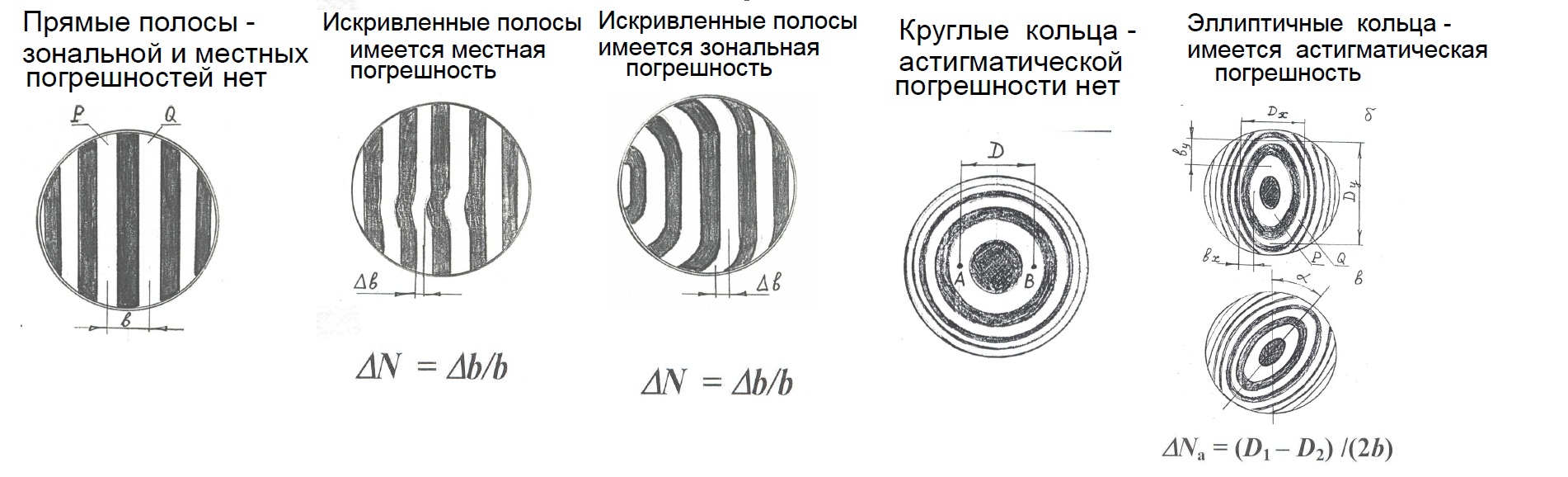
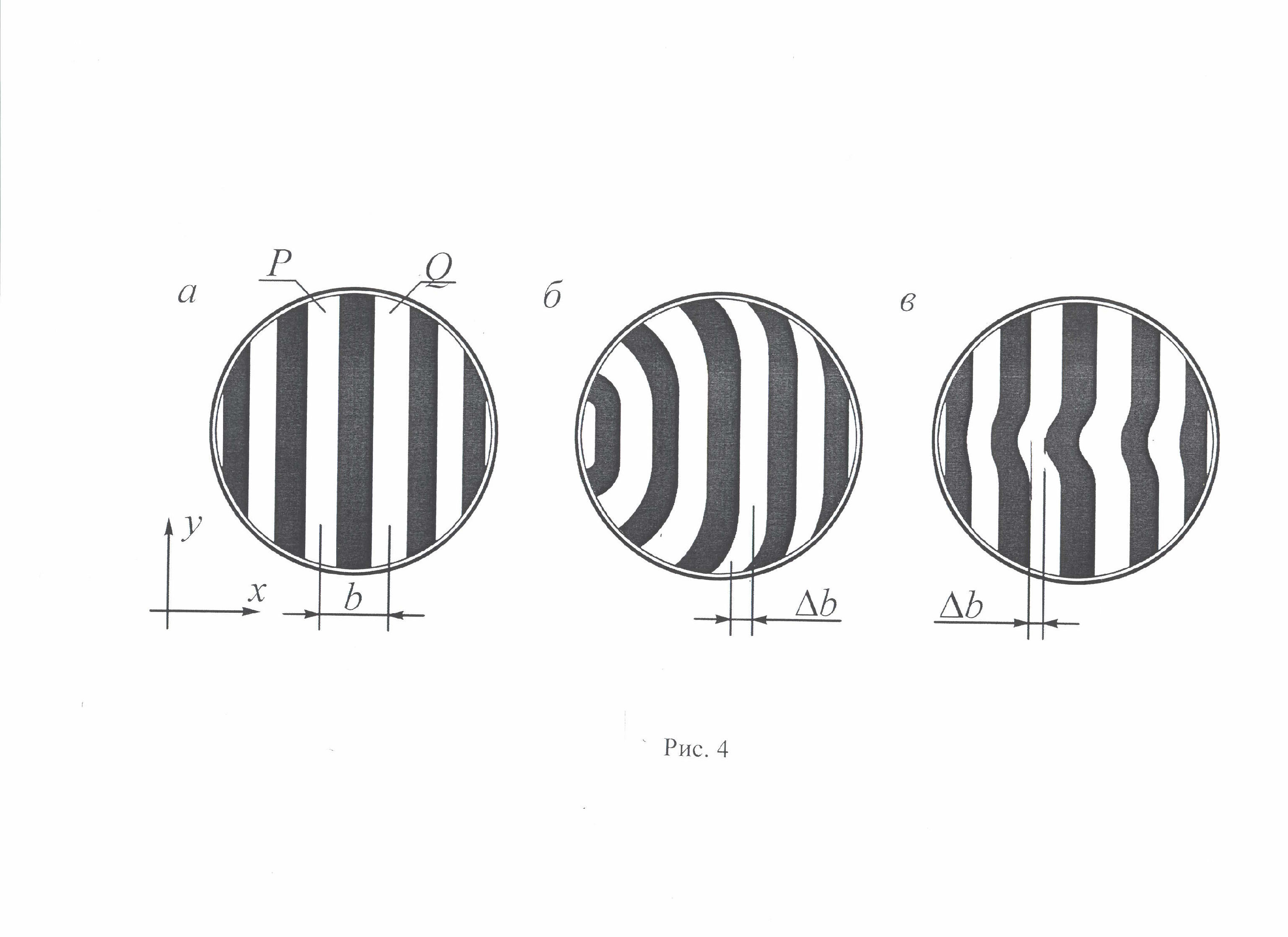
1. Деформация волнового фронта при взаимодействии с поверхностью, имеющей погрешность. Типовые погрешности формы оптических поверхностей и соответствующие им типовые интерферограммы.

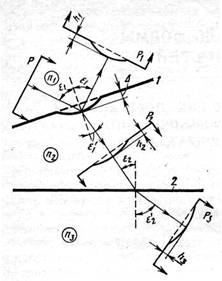
Классификация типов погрешностей:

1) общая;

2) местная;

3) зональная;

4) астигматическая.

Общая погрешность – это такое отклонение поверхности, при котором сохраняется вид поверхности. Например, сферическая поверхность остается сферой, но её радиус не соответствует номиналу. Плоская поверхность может превратиться в сферу с очень большим радиусом кривизны.

М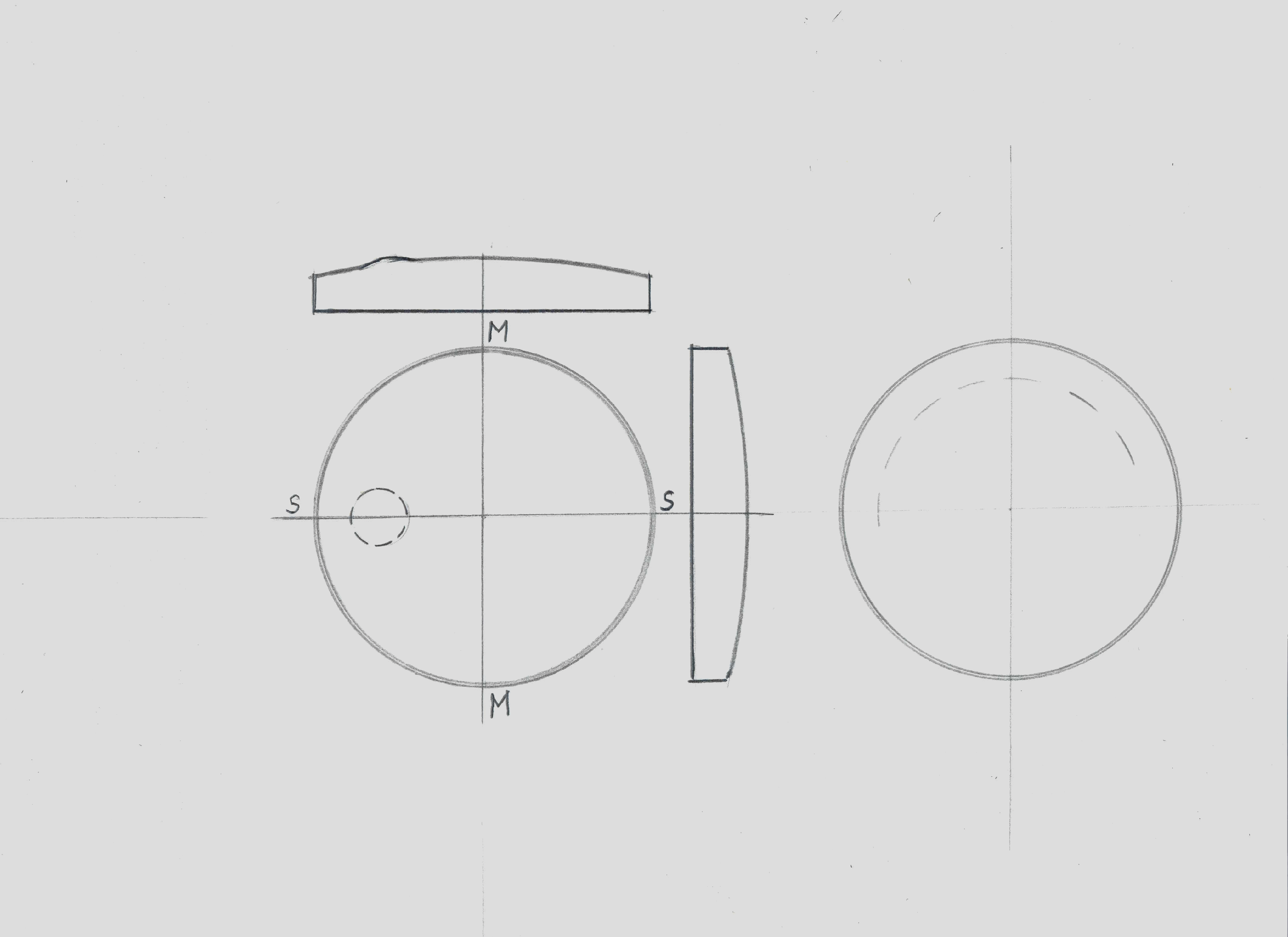 естной погрешностью называют локальное отклонение отдельного участка оптической поверхности от её теоретического вида. Местные погрешности локализованы на небольшом участке оптической поверхности. Типичные примеры местных погрешностей – это «яма» или «бугор», расположенные в произвольном месте оптической поверхности. Местные погрешности характерны для поверхностей любых размеров, обрабатываемых как в одиночку, так и блоками.

Зональной погрешностью называют такое отклонение поверхности от её теоретического вида, при котором её осевая симметрия не нарушается. Типичный пример зональной погрешности – это «завал края», при котором на краю оптической детали форма реальной поверхности резко отличается от теоретической.

Зональные погрешности

характерны для поверхностей

крупногабаритных оптических

деталей, которые обрабатывают

в одиночку.

Астигматической погрешностью называют такое отклонение поверхности от её теоретического вида, при котором нарушается её осевая симметрия. Оптическая поверхность приобретает отклонения формы, которые различны в разных направлениях от вершины поверхности к её краям. Из осесимметричной оптическая поверхность превращается в поверхность с двумя осями симметрии :

Астигматические погрешности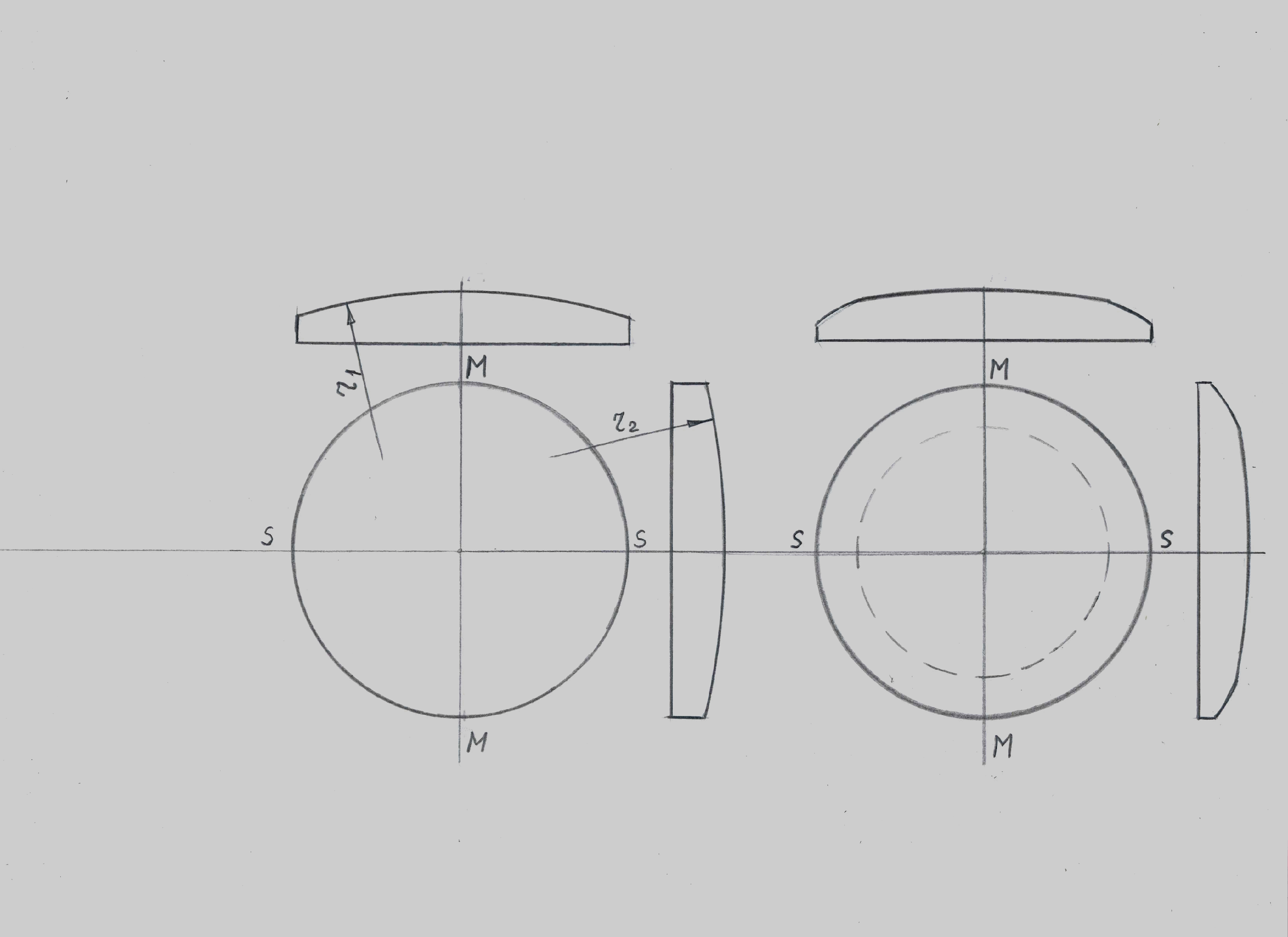

характерны для поверхностей

крупногабаритных оптических

деталей, которые обрабатывают

в одиночку.

2. Способы регистрации интерференционных картин, полученных при контроле формы оптических поверхностей. Амплитудный метод обработки интерферограмм, его достоинства и недостатки.

Интерферограмма, полученная в результате взаимодействия эталонного и рабочего волновых фронтов, содержит в себе информацию об искажениях рабочего волнового фронта, так как эталонный фронт имеет идеальную форму. Эта информация закодирована в форме интерференционных полос или колец.

В идеальном случае рабочий волновой фронт искажен только погрешностями формы контролируемой поверхности.

Реально рабочий волновой фронт может получить дополнительные искажения из-за погрешностей элементов оптической системы интерферометра. В таком случае необходимо учитывать эти искажения:

- либо расчетным путем,

- либо по результатам аттестации оптической системы интерферометра.

Эталонный волновой фронт также может иметь искажения, которые нужно учитывать. Обработку интерференционных картин осуществляют амплитудным или фазовым методами.

Фазовый метод обработки интерференционных картин может применяться только при фотоэлектрической регистрации поля интерференции. Он основан на получении информации о разности фаз двух переменных электрических сигналов, один из которых идет от анализируемой точки поля интерференции, а другой из некоторой постоянной опорной точки поля.

Фазовый метод точнее амплитудного.

Для реализации фазового метода необходимо обеспечить постоянное изменение разности хода интерферирующий пучков по определенному закону, что не всегда технически осуществимо.

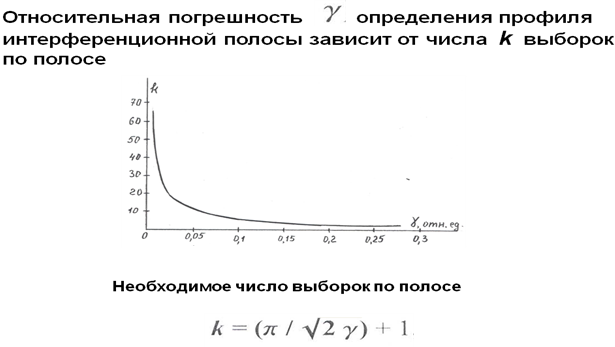
Зафиксированная на приемник излучения интерференционная картина называется интерферограммой. Интерферограмму можно обрабатывают классическим амплитудным методом или с помощью дискретного преобразования Фурье.

При классической реализации амплитудного метода определяют координаты хребтовых линий интерференционных полос или колец - точек, где расположены максимумы интерференции. Далее учитывают то, что соседние максимумы интерференции расположены там, где оптическая разность хода между интерферирующими лучами составляет длину волны излучения .

Раньше интерферограммы фотографировали на фотопленку, а затем по негативу находили координаты точек хребтовых линий с помощью приборов для измерения линейных размеров. В настоящее время для регистрации интерферограмм применяют координатно-чувствительные приемники, которые фиксируют значения оптического сигнала в отдельных точках поля интерференции.

Основные требования к приемникам излучения:

• высокая чувствительность,

• высокая разрещающая способность.

ПРОБЛЕМЫ регистрации и обработки интерферограмм

1. При регистрации интерферограммы нужно обеспечить оптическое сопряжение плоскости, где расположена контролируемая поверхность, с плоскостью приемника излучения. Тогда интерферограмма будет «наложена» на контролируемую поверхность и ее вид будет соответствовать погрешностям формы контролируемой поверхности. Для решения этой проблемы в интерферометре необходим объектив сопряжения.

Передний фокус объектива сопряжения должен совпадать с автоколлимационной точкой интерферометра, чтобы на приемник излучения поступали плоские волновые фронты

2. При контроле формы сферических и асферических поверхностей с большой числовой апертурой интерферограмма расположена на сфере, а ее изображение регистрируется плоской чувствительной площадкой приемника излучения. Из-за этого нарушается подобие между интерферограммой и ее изображением, то есть возникает дисторсия, которую нужно компенсировать дисторсией объектива сопряжения.

3. Для точного определения координаты х и у дискретных точек хребтовых линий интерференционных полос важны высокий контраст и чистота интерференционного поля. Поэтому применяют фильтрацию интерферограмм.

3. Измерение формы плоских поверхностей малого и среднего диаметров на интерферометрах, построенных по схеме Физо. Конструктивные особенности интерферометров. Анализ факторов, влияющих на точность измерений.

В оптических приборах многие детали содержат плоские поверхности. Они могут принадлежать призмам, зеркалам, пластинам и линзам. При малых и средних диаметрах плоские поверхности не вызывают проблем при организации их контроля. Но с увеличением диаметра проблема контроля плоскостей значительно усложняется.

Кроме пробных стекол для контроля плоскостей целесообразно применять интерферометр Физо.

Главная особенность интерферометра Физо заключается в том, что интерференционные явления возникают в тонком воздушном промежутке между плоскими поверхностями при нормальном падении лучей на эти поверхности. В связи этим интерферометры Физо виброустойчивы и их можно эксплуатировать в цеховых условиях.

Старые модели таких интерферометров не имели устройств для регистрации интерферограмм. Исследования проводились визуально, что снижало точность контроля поверхностей. По мере развития фототехники стали применять фоторегистрацию интерференционных картин с последующей обработкой негативов на измерительном микроскопе. В настоящее время изображение интерференционной картины проецируют на координатный фотоприемник, что дает возможность одновременно видеть картину на экране монитора и выполнять ее автоматизированную обработку.

Классический вариант интерферометра Физо с линзовым коллиматором хорошо подходит для контроля плоскостей диаметром до 150 мм. В таком случае роль линзового коллиматора может играть двухлинзовый объектив, а при малых диаметрах одиночная линза, рассчитанная на минимум сферической аберрации. Проблем с изготовлением эталонной пластины также не возникает. Для выведения из поля интерференции вредного пучка лучей, отраженных верхней поверхностью эталонной пластины, ее делают клиновидной.

ИНТЕРФЕРОМЕТР ФИЗО С ЛИНЗОВЫМ КОЛЛИМАТОРОМ 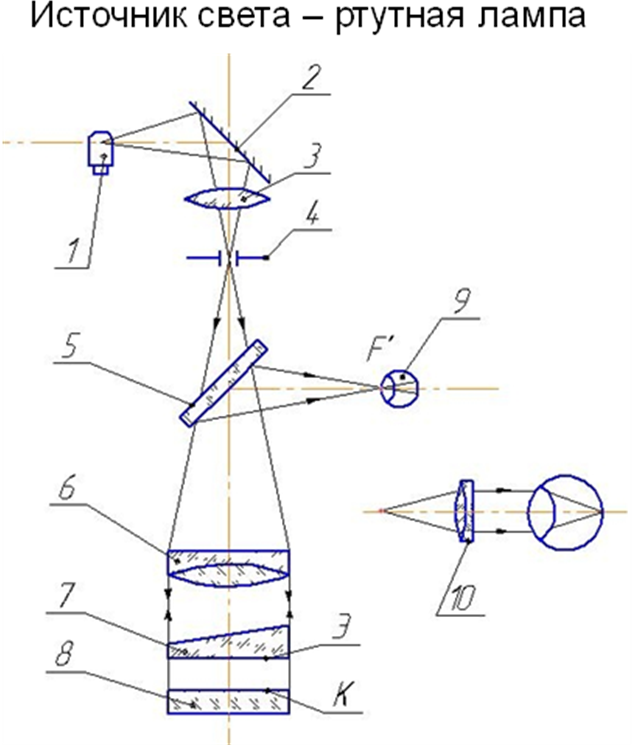По такой схеме (до 1976 г.) изготовлены интерферометры с для контроля плоскостей малых и средних диаметров: ИТ-40, ИТ-70, ИТ-87,

ИТ-100. Цифра в маркировке означает максимальный диаметр контролируемых плоскостей.

При контроле плоскостей без покрытий эталонная пластина также без покрытия, и интерферометр работает в режиме двухлучевой интерференции. В таком случае при визуальном контроле выявляют погрешности плоскостей порядка

Если на контролируемую поверхность нанесено отражающие покрытие, то п рименяют эталонную пластинку с полупрозрачным покрытием: тогда интерферометр работает в режиме многолучевой интерференции, при которой чувствительность контроля на порядок выше.

Для установки контролируемой плоскости параллельно эталонной плоскости интерферометра деталь помещают на специальный качающийся столик. Винты столика позволяют качать деталь, благодаря чему интерференционную картину выводят на «ровное поле» или полосы конечной толщины.

4. Измерение формы плоских поверхностей большого диаметра на интерферометрах, построенных по схеме Физо. Конструктивные особенности интерферометров. Анализ факторов, влияющих на точность измерений.

ИНТЕРФЕРОМЕТРЫ ФИЗО С ЗЕРКАЛЬНЫМИ КОЛЛИМАТОРАМИ

Увеличение диаметров контролируемых плоскостей

привело к созданию интерферометров Физо с зеркальными коллиматорами. Применяют сферические зеркала с малыми относительными отверстиями и параболические зеркала:

• сферическое зеркало вносит малые сферические аберрации при относительном отверстии D:f’ < 1:10;

• параболическое зеркало не вносит сферическую аберрацию при любых относительных отверстиях.

Достоинство зеркальных коллиматоров – возможность получения параллельных пучков большого диаметра.

Недостаток зеркального коллиматора – экранирование центральной зоны пучка.

Пучок без центрального экранирования создают внеосевые параболоиды.

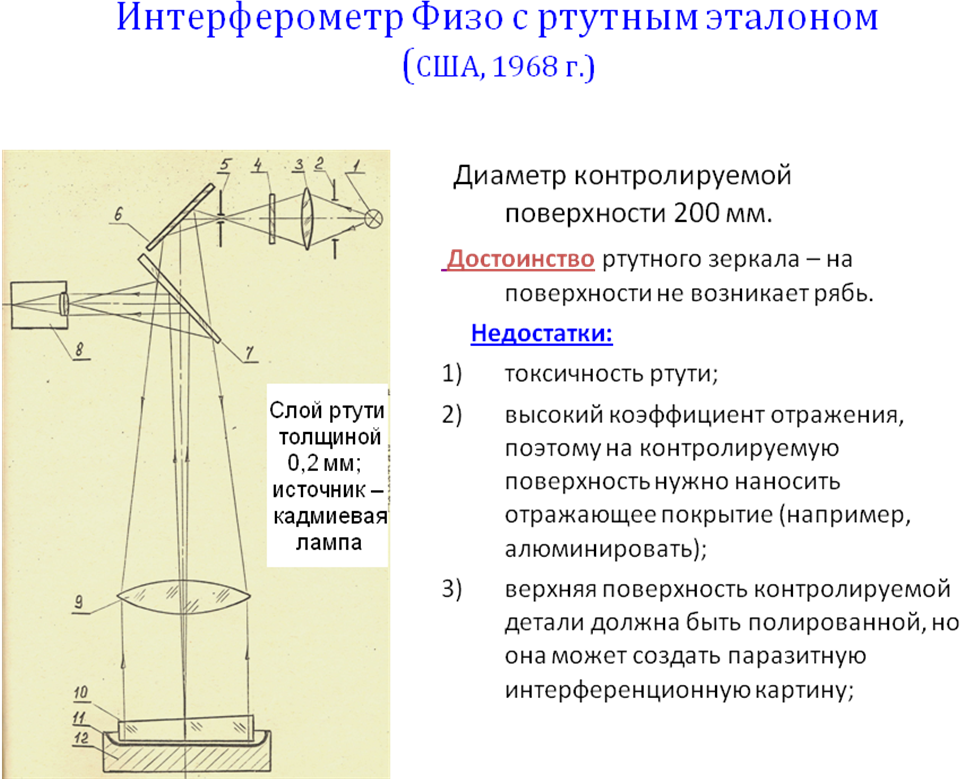
• Идея использования жидкости в качестве плоского зеркала принадлежит Рэлею.

Важно, чтобы жидкость не была смесью, так как может произойти её расслоение, в результате в разных зонах будут различные значения коэффициентов преломления и отражения. Используют: дистилированую воду, глицерин, масла, ртуть.

• Недостатки жидкостных эталонов:

1) Виброзависимость – образование ряби на поверхности (предпочтительно использовать вязкие жидкости);

2) Искажение поверхности пылинками и соринками, осевшими на неё;

3) Искажение поверхности жидкости вблизи стенок сосуда.

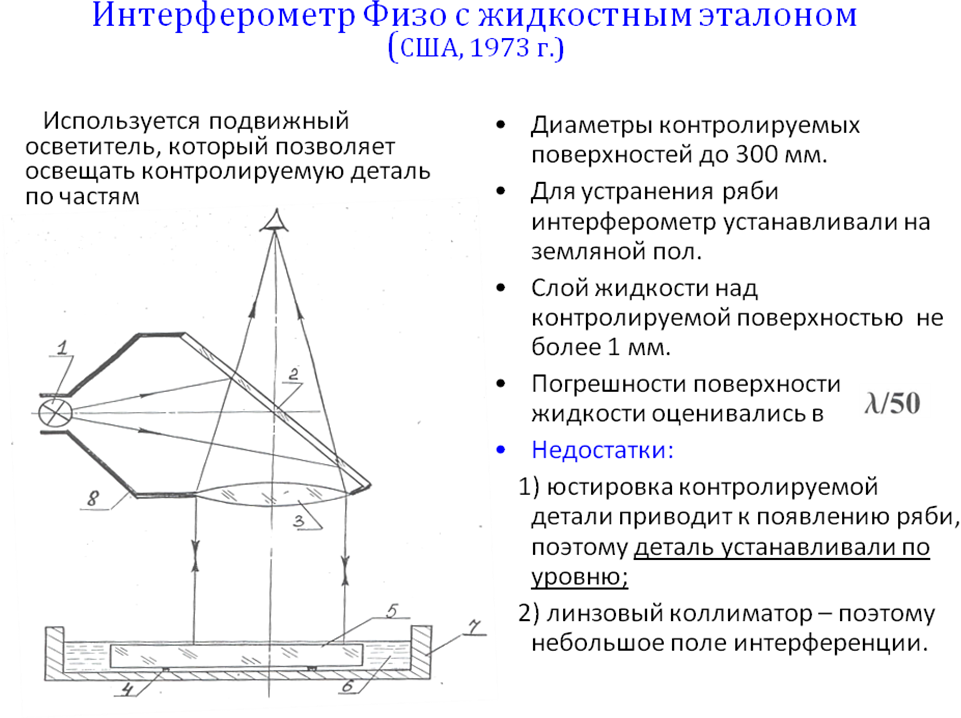
Рекомендации по применению жидкостного эталона плоскости в интерферометрах Физо:

• Виброизолировать и термостатировать интерферометр.

• Использовать вязкие и нетоксичные жидкости: глицерин, минеральные масла и отбеленное касторовое масло.

• Не допускать смеси жидкостей и загрязнения поверхности жидкости пылью и соринками.

• Регистрировать интерференционные картины многократно с наименьшим временем считывания.

• Сосуд для жидкости должен быть большего диаметра, чем диаметр контролируемой плоскости, чтобы искажение поверхности жидкости вблизи стенок сосуда не влияло на вид интерферограмм.

• При обработке интерферограмм учитывать сферичность жидкости.

5. Измерение формы плоских поверхностей большого диаметра методом Коммона. Конструктивные особенности интерферометра. Анализ факторов, влияющих на точность измерений.

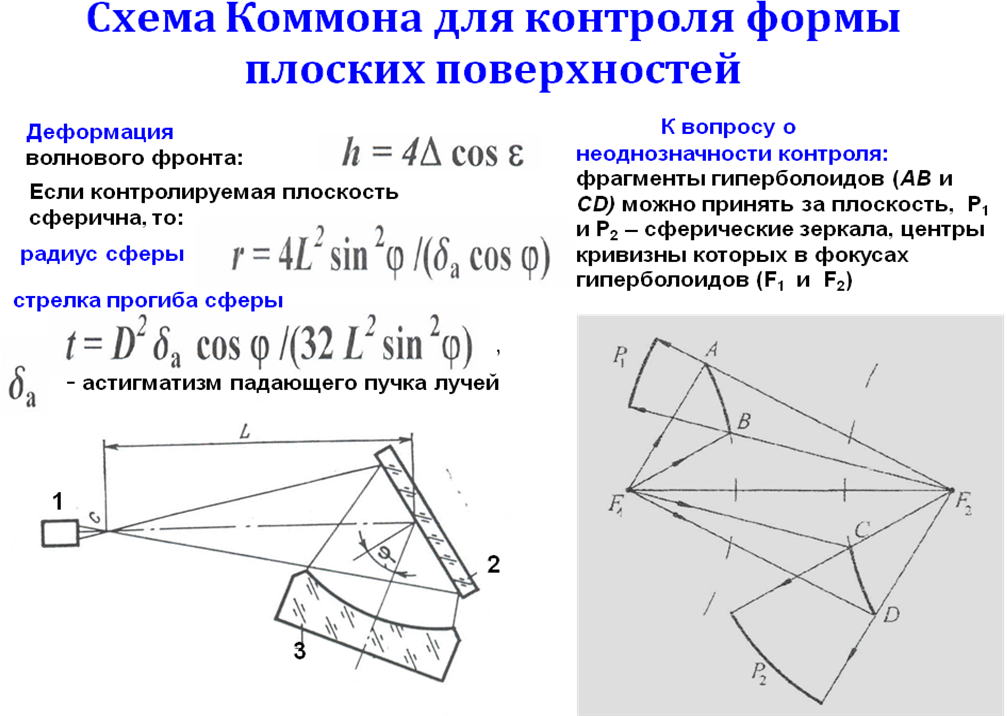
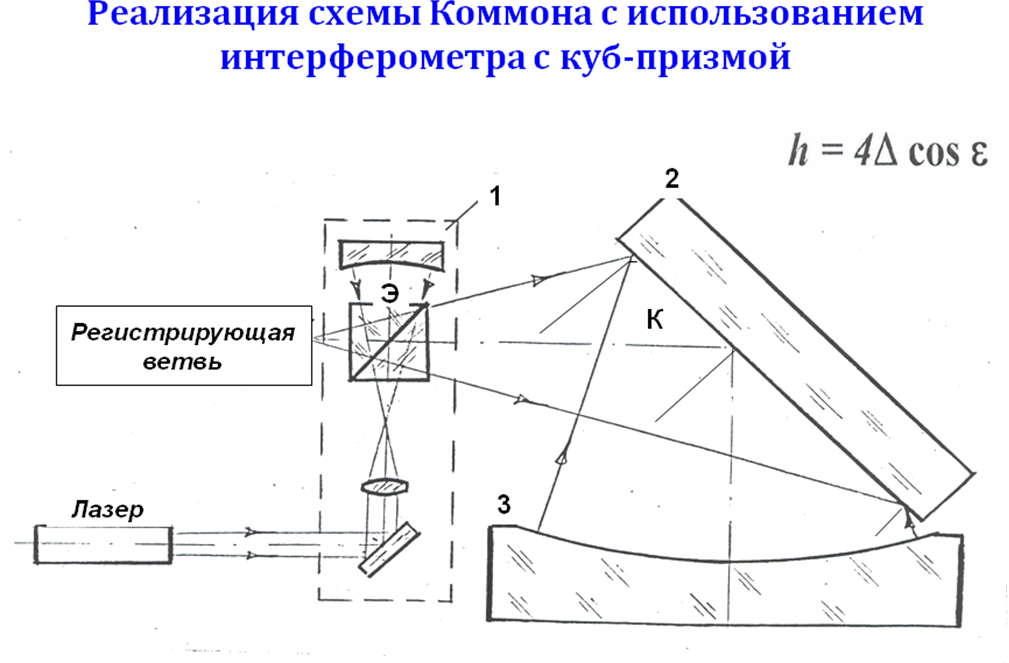
Достоинства: возможность контроля плоскостей большого диаметра с малым эталоном и высокая чувствительность контроля из-за двойного отражения лучей от контролируемой поверхности.

Недостатки:

1. Неоднозначность контроля: за плоскость может быть принят фрагмент гиперболоида;

2. Неодинаковая чувствительность к погрешностям контролируемой поверхности, расположенным на разных расстояниях от её центра, так как углы падения лучей различны;

3. Образование «ложного» астигматизма ( ), если контролируемая поверхность оказалась сферой с большим радиусом кривизны.

6. Измерение формы вогнутых сферических поверхностей на интерферометре с куб-призмой. Конструктивные особенности интерферометра. Анализ факторов, влияющих на точность измерений, способы устранения некоторых факторов.

Для контроля сферических поверхностей оптических деталей используют интерферометры типа Физо и Тваймана - Грина.

Роль эталонных элементов таких интерферометров играет сферическая поверхность зеркала или линзы, на которую направляют гомоцентрический пучок лучей, причем вершина пучка совмещена с центром кривизны эталонной поверхности. Поэтому лучи падают на эталонную поверхность по нормалям и отражаются в обратном направлении.

Интерферометры для контроля сферических поверхностей входят в состав информационно-измерительных систем, что обеспечивает автоматизированную обработку результатов измерений в реальном масштабе времени и представления результатов измерения в виде, оптимальном для дальнейшего использования.

Интерферометр Тваймана – Грина для контроля вогнутых сфер (1969 г.)

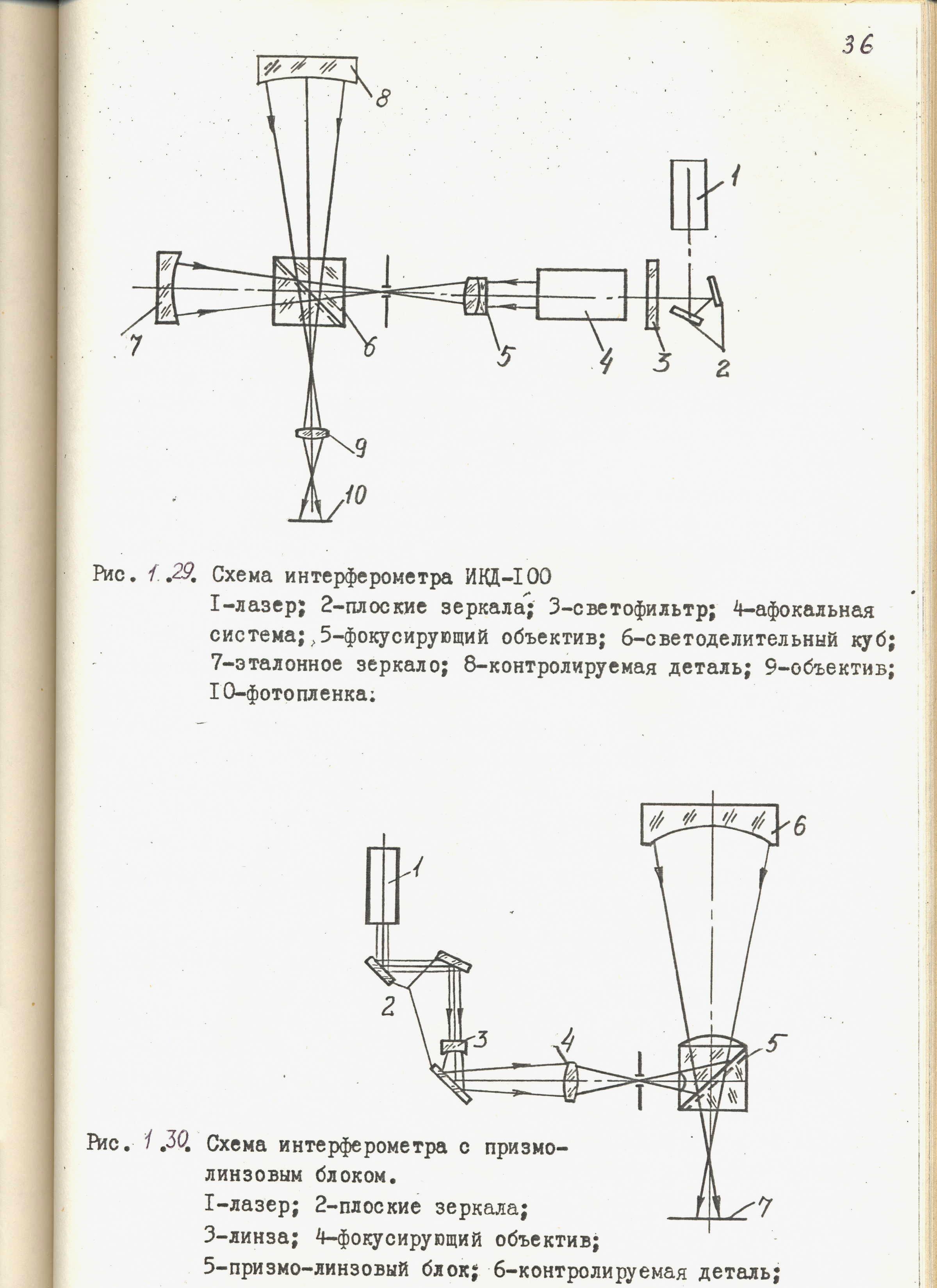
По такой схеме построены интерферометры ИТ-172 и ИКАД-100, которые называют интерферометрами с куб-призмой. Максимальная числовая апертура контролируемых на интерферометрах вогнутых сфер составляет 0,2 … 0,25. Блик на интерферограмме возникает из-за отражений лучей от граней куб-призмы.

Наклон куб-призмы к оси пучка лучей, а также её клиновидность приводят к появлению инструментальной астигматической погрешности, которая пропорциональна квадрату угла наклона

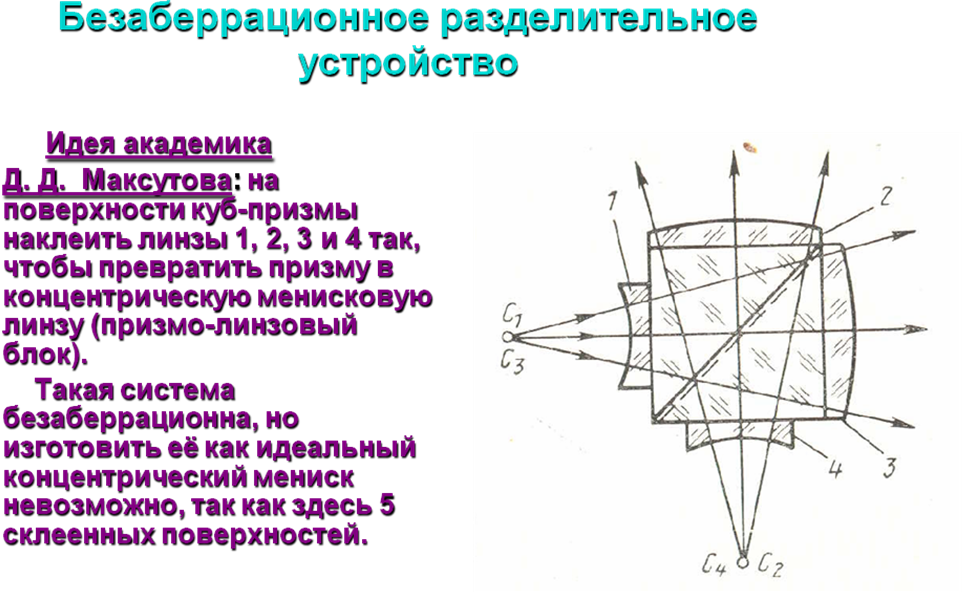
Интерферометр с призмо-линзовым блоком:

Интерферометр построен по схеме Физо. Роль эталона здесь играет выпуклая поверхность плоско-выпуклой линзы. Диапазон числовых апертур контролируемых поверхностей расширен до 0,3.

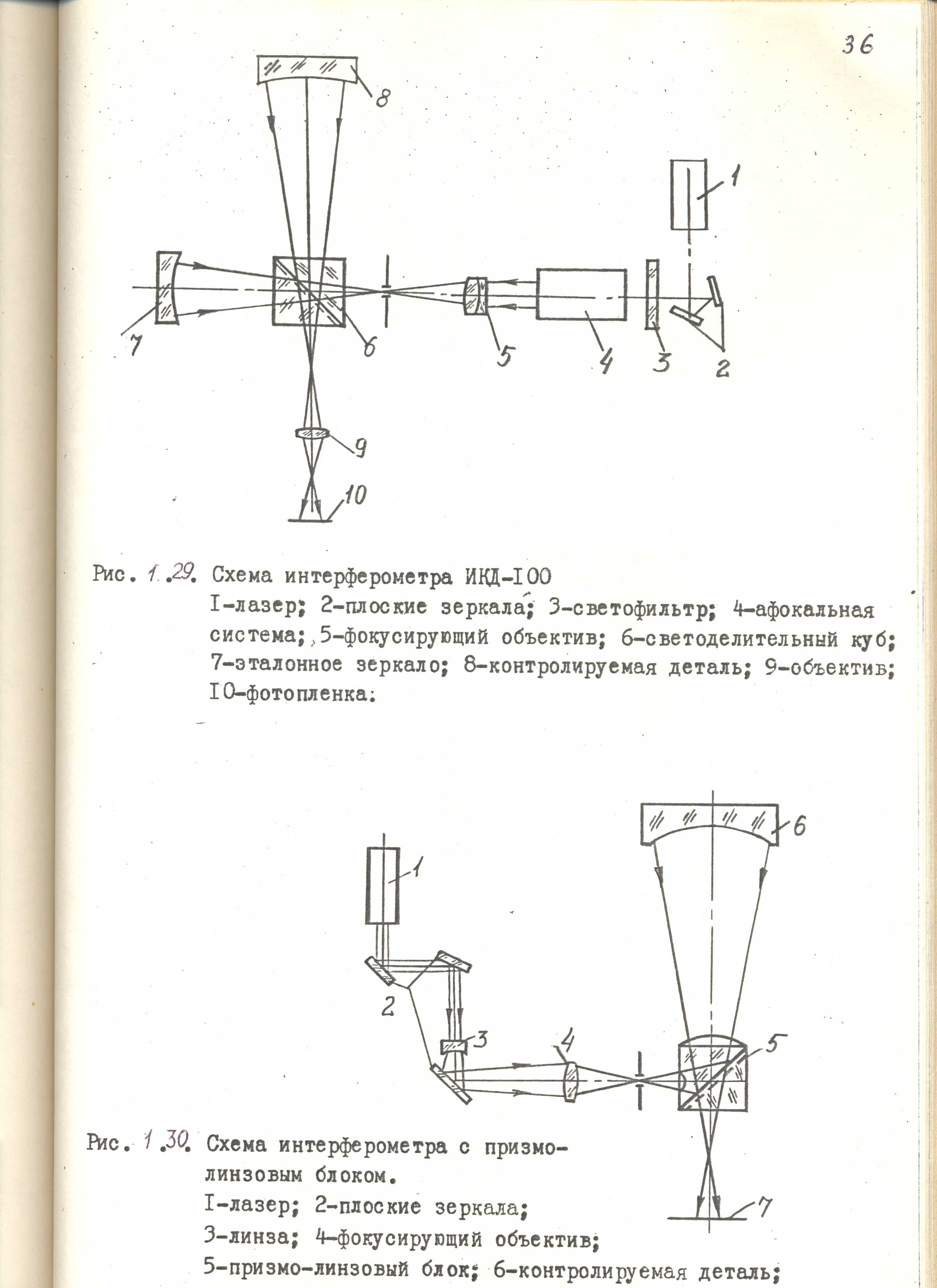
7. Измерение формы вогнутых сферических поверхностей на интерферометре с квазиапланатическим мениском. Конструктивные особенности интерферометра. Анализ факторов, влияющих на точность измерений.

Вносимая куб-призмой

аберрация

скомпенсирована

вогнутой поверхностью

мениска. На выпуклую

поверхность мениска лучи падают по нормалям; она выполняет роль эталона.

К расчету радиуса кривизны компенсирующей поверхности квазиапланатического мениска:

Достоинства:

1) построен по схеме Физо, поэтому между контролируемой и эталонной поверхностями только воздух;

2) обеспечивает контроль высокоапертурных поверхностей при том, что числовая апертура пучка в осветительной и регистрирующей ветвях невелика;

3) нарушение величины воздушного промежутка по отношению к расчетному не приводит к нарушению состояния аберрационной коррекции;

3) основное требование к установке мениска относительно

куб-призмы – перпендикулярность оси мениска к грани

куб-призмы;

4) погрешности изготовления куб-призмы не влияют на вид интерференционной картины, так как она расположена до разделения пучка на эталонный и рабочий.

Недостаток: по мере увеличения числовой апертуры рабочего пучка лучей ухудшается технологичность мениска.

8. Измерение формы вогнутых сферических поверхностей на светосильном интерферометре с апланатическим мениском. Конструктивные особенности интерферометра. Анализ факторов, влияющих на точность измерений.

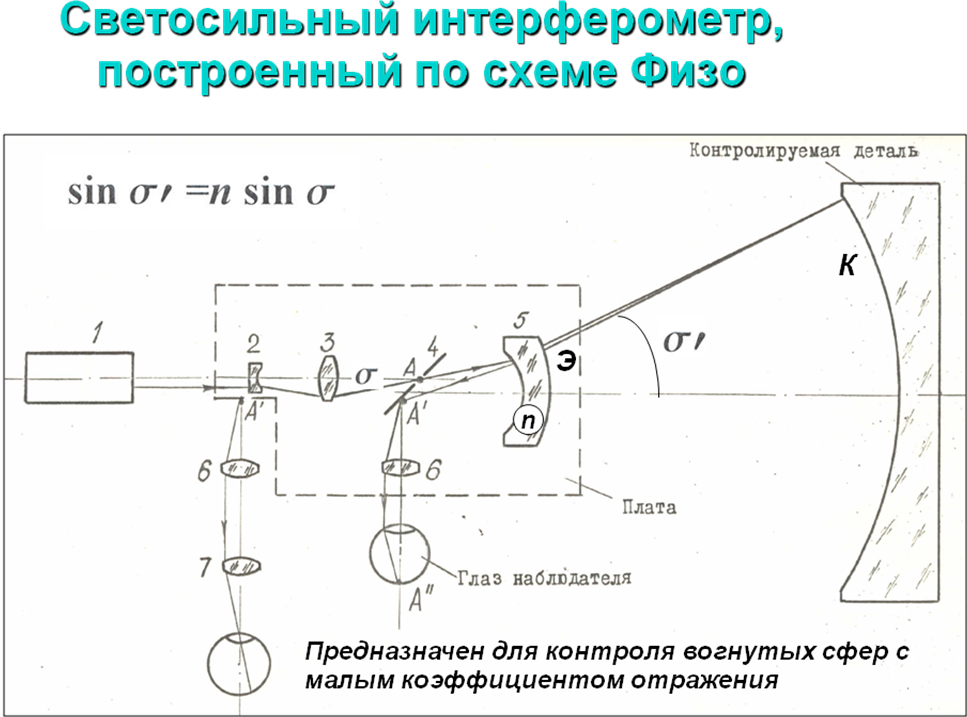
Достоинства:

1) построен по схеме Физо, поэтому между контролируемой и эталонной поверхностями только воздух;

2) пригоден для контроля просветленных высокоапертурных сферических поверхностей, так как в нем нет полупрозрачных элементов;

3) имеет набор апланатических менисков с разными коэффициентами отражения эталонных поверхностей, что позволяет получить контрастную интерференционную картину.

Недостаток: лучи падают на апланатический мениск их внеосевой точки, поэтому возникает инструментальная астигматическая погрешность (ложный астигматизм). При числовой апертуре контролируемых поверхностей 0,5 астигматическая погрешность составляет

9. Измерение формы вогнутых и выпуклых сферических поверхностей малого и среднего диаметров на интерферометре Коломийцова - Духопела. Конструктивные особенности интерферометра. Анализ факторов, влияющих на точность измерений.

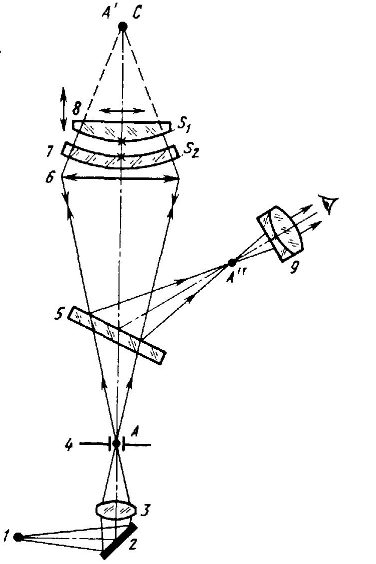
10. Измерение формы выпуклых сферических поверхностей большого диаметра на интерферометре ДВИН-600. Конструктивные особенности интерферометра. Анализ факторов, влияющих на точность измерений.

r_1э = - 1698,2 мм

r_2э = - 2512 мм

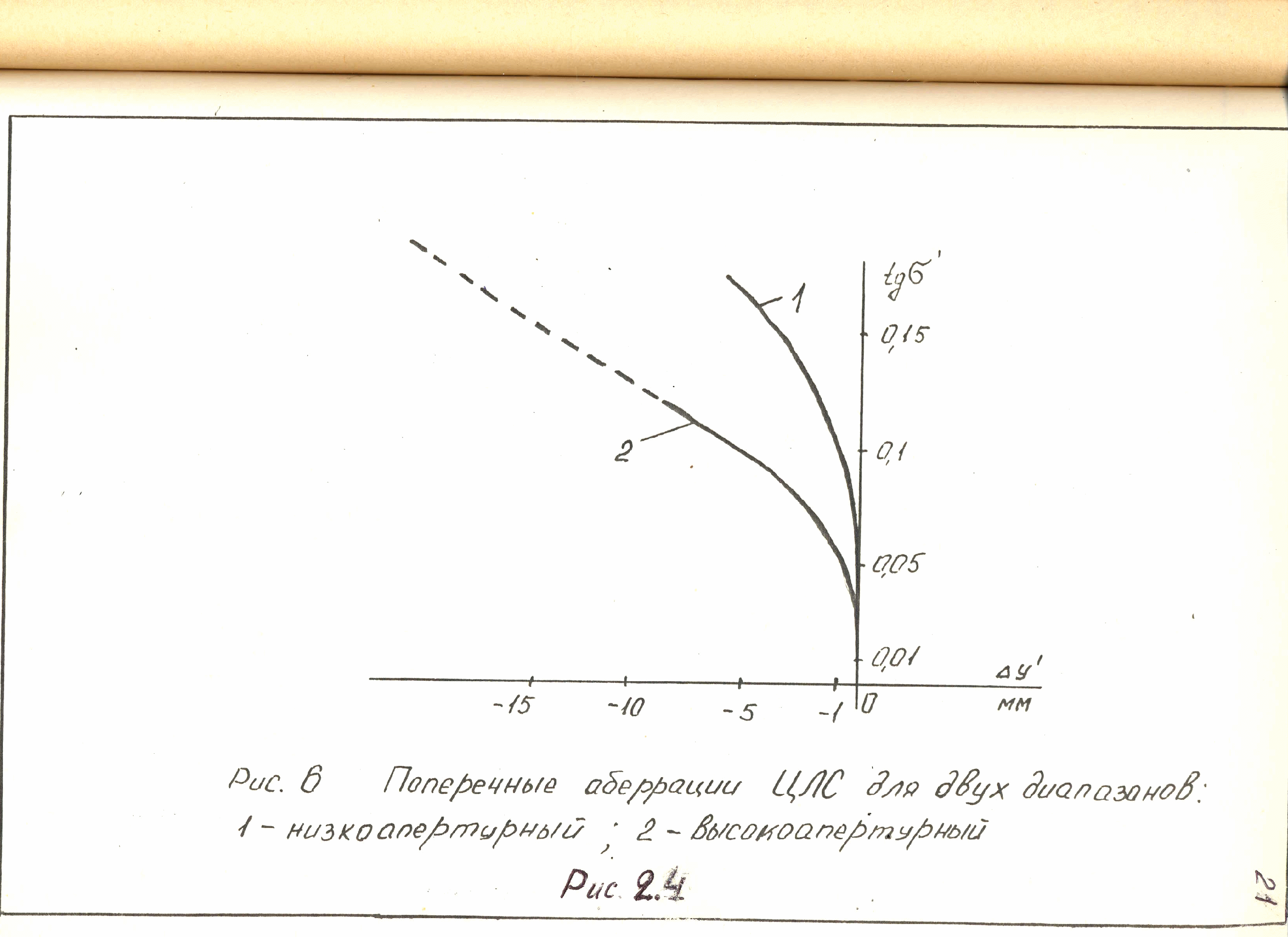
Модернизированный вариант интерферометра ДВИН-600 (1980 г.)

1. И змерение формы выпуклых поверхностей крупногабаритных линз на интерферометре ИКАП с использованием крупногабаритного эталонного зеркала. Конструктивные особенности интерферометра. Анализ факторов, влияющих на точность измерений.

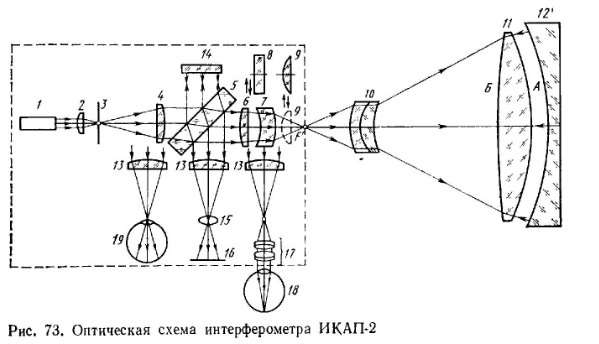
2. Измерение формы параболических поверхностей методом анаберрационных точек. Конструктивные особенности интерферометра. Анализ факторов, влияющих на точность измерений.

Отражающие эллипсоиды, параболоиды и гиперболоиды обладают парами оптически сопряженных анаберрационных точек, которые расположены в их геометрических фокусах.

Лучи света, вышедшие из одной из анаберрационных точек, после отражения от АП собираются в другой анаберрационной точке не приобретая аберраций.

Метод анаберрационных точек основан на анализе формы волнового фронта, который образовался при участи исследуемой АП, при условии хода лучей через ее анаберрационные точки.

Для реализации метода необходимо создать автоколлимационную систему, которая при идеально выполненной АП образует строго сферический волновой фронт.

Возможность реализации метода определяется параметрами контролируемой АП, которые влияют на конструктивные параметры вспомогательных элементов измерительной ветви интерферометра.

В обоих случаях использована анаберрационная точка параболоида, которая одновременно

является его геометрическим и оптическим фокусом. Значение апертурного угла для лучей, идущих из края параболоида в фокус, вычисляют через его тангенс

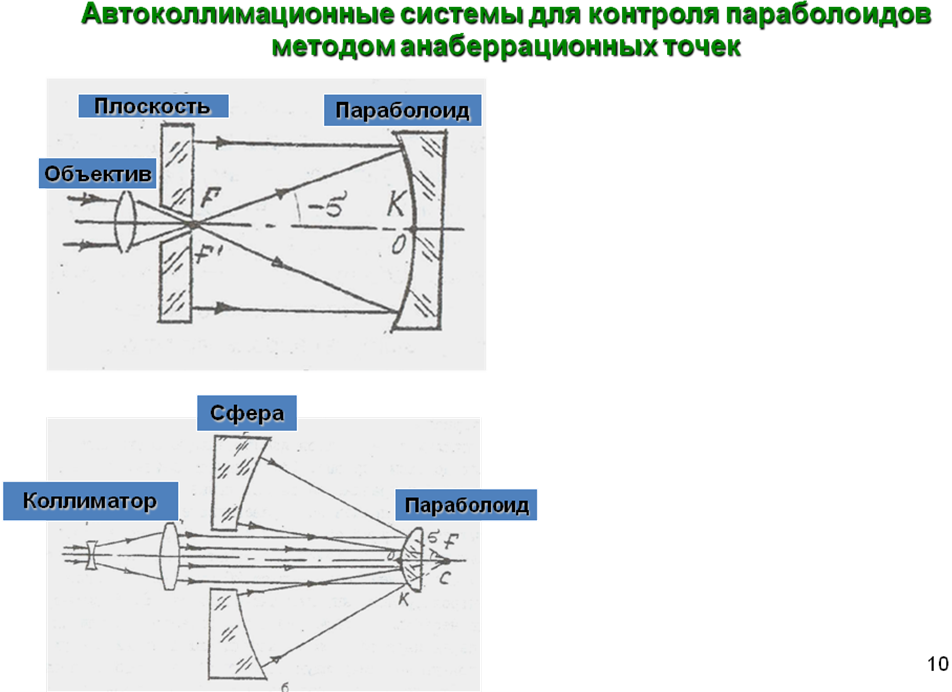
В случае вогнутых параболоидов

(рис. а) на параболоид падает

расходящийся гомоцентрический пучок

лучей, вершина которого находится в

фокусе безаберрационного объектива 5.

Задний фокус F объектива 5 совмещен с

фокусом параболоида (точкой F). Для

автоколлимации пучка здесь используется плоское зеркало 7 с отверстием. Диаметр Dн

неконтролируемой зоны параболоида в данном случае равен диаметру отверстия в зеркале: Dн

=Dотв . Чтобы отверстие в зеркале имело минимальный диаметр, необходимо устанавливать

зеркало в фокальной плоскости параболоида, тогда толщина d воздушного промежутка между

параболоидом и плоским зеркалом равна отрезку OF . Расстояние в от гиперболоида до фокуса

объектива 5 также равно отрезку OF . В отличие от вспомогательного сферического зеркала, которое используется для контроля гиперболоидов, плоское зеркало здесь может быть универсальным. Важно, чтобы его диаметр был не меньше, чем диаметр контролируемого

параболоида. При наличии достаточно большого плоского зеркала (например, диаметром I м) возможно обеспечить контроль вогнутых параболоидов, диаметр которых не более

одного метра. За пределами этого диаметра, как правило, контроль вогнутых параболоидов методом анаберрационных точек не осуществляется из-за проблем с плоским зеркалом.

Для выпуклых параболоидов измерительную ветвь интерферометра строят по схеме на рис. б. В данном случае на измеряемый параболоид 6 направляется параллельный пучок лучей, причем диаметр этого пучка должен быть равен диаметру параболоида. Параллельный пучок лучей создается в интерферометре коллимирующей системой. Диаметр коллимированного пучка на выходе из нее не превышает 20 мм, что ограничивает диаметр контролируемых выпуклых параболоидов. Если диаметр параболоида несколько больше, то в измерительной ветви интерферометра перед параболоидом устанавливают дополнительную безаберрационную коллимирующую систему 5', как это показано на рис. б. Эту дополнительную систему обычно строят по принципу трубы Галилея, так как при достаточно простой двухлинзовой конструкции в ней успешно исправляется сферическая аберрация.

3. Измерение формы гиперболических поверхностей методом анаберрационных точек. Конструктивные особенности интерферометра. Анализ факторов, влияющих на точность измерений.

Отражающие эллипсоиды, параболоиды и гиперболоиды обладают парами оптически сопряженных анаберрационных точек, которые расположены в их геометрических фокусах.

Лучи света, вышедшие из одной из анаберрационных точек, после отражения от АП собираются в другой анаберрационной точке не приобретая аберраций.

Метод анаберрационных точек основан на анализе формы волнового фронта, который образовался при участи исследуемой АП, при условии хода лучей через ее анаберрационные точки.

Для реализации метода необходимо создать автоколлимационную систему, которая при идеально выполненной АП образует строго сферический волновой фронт.

Возможность реализации метода определяется параметрами контролируемой АП, которые влияют на конструктивные параметры вспомогательных элементов измерительной ветви интерферометра.

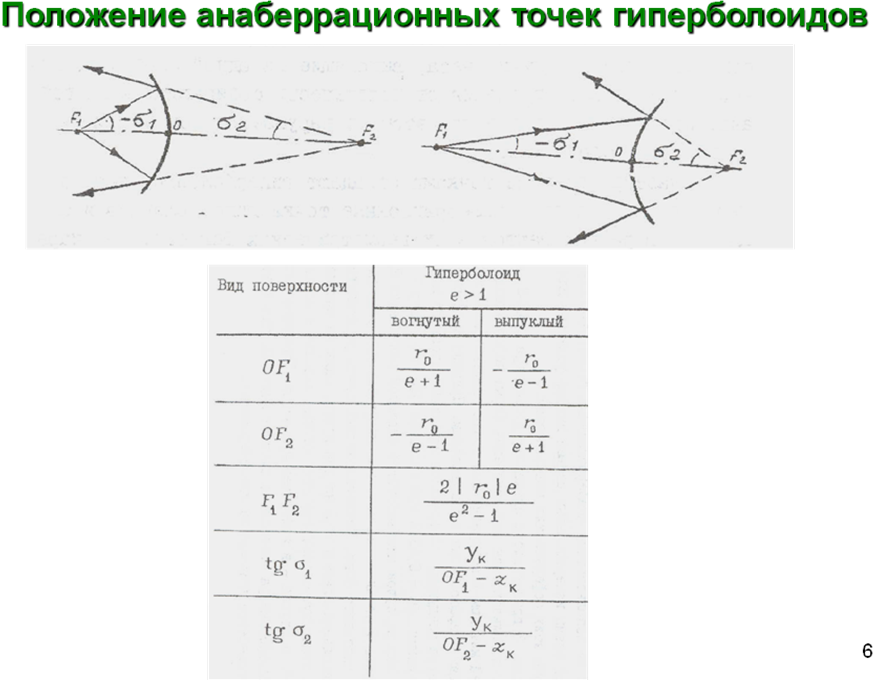
Постоянным элементом измерительной ветви является безаберрационный объектив 5,

задний фокус F' которого (см. рис. а и б) совмещен с одним из фокусов F контролируемого гиперболоида 6. Гомоцентрический пучок лучей, выходящий из объектива 5, отражается от поверхности К, в результате чего образуется расходящийся гомоцентрический пучок с вершиной в точке F . Чтобы вернуть излучение в интерферометр, установлено вогнутое сферическое зеркало 7 с отверстием, центр кривизны (точка С) которого совмещен с точкой F . В результате происходит полная автоколлимация лучей без нарушения гомоцентричности пучка в случае, если контролируемая поверхность является гиперболоидом.

Рабочая интерференционная картина образуется вследствие взаимодействия

двух плоских волновых фронтов, которые вышли из эталонной и измерительной

ветвей интерферометра. В регистрирующей ветви интерферометра установлены

фокусирующий объектив 8, объектив сопряжения 9, ПЗС-матрица 10 и

электронная часть II, включающая систему визуализации и автоматизированной

обработки интерферограмм. При необходимости фотографирования интерферен-

ционной картины вместо элементов 9, 10 и II устанавливает; фотоаппарат 12,

через визир которого оператор может наблюдать интерференционную картину.

Сферическое зеркало 7 практически всегда является элементом индивидуального

назначения. Так как зеркало имеет отверстие для прохода лучей к

контролируемому гиперболоиду, очевидно, что в центре гиперболоида образуется

неконтролируемая зона. Размер этой зоны зависит от диаметра отверстия на

зеркале. Чтобы размер неконтролируемой зоны был минимальным, нужно вы-

полнять отверстие коническим, а вершину сферического зеркала совмещать с

фокусом объектива 5. В таком случае однозначно определяется связь значения

радиуса з r кривизны зеркала 7 с параметрами 0 r и е гиперболоида. Очевидно, что

Преимуществами схемы, представленной на рис. в, перед схемой на рис. б

можно считать:

1. отсутствие неконтролируемой зоны;

2. соизмеримый с диаметром контролируемого гиперболоида диаметр

менисковой линзы

Вместе с тем, схема на рис. в имеет существенные недостатки:

1. высокие требования к однородности стекла и форме поверхностей линзы,

в то время как она имеет индивидуальное назначение;

2. большие потери света, так как в отличие от схемы с зеркалом здесь не

может быть отражающего покрытия на вогнутой поверхности мениска.

4. Измерение формы эллиптических поверхностей методом анаберрационных точек. Конструктивные особенности интерферометра. Анализ факторов, влияющих на точность измерений.

Отражающие эллипсоиды, параболоиды и гиперболоиды обладают парами оптически сопряженных анаберрационных точек, которые расположены в их геометрических фокусах.

Лучи света, вышедшие из одной из анаберрационных точек, после отражения от АП собираются в другой анаберрационной точке не приобретая аберраций.

Метод анаберрационных точек основан на анализе формы волнового фронта, который образовался при участи исследуемой АП, при условии хода лучей через ее анаберрационные точки.

Для реализации метода необходимо создать автоколлимационную систему, которая при идеально выполненной АП образует строго сферический волновой фронт.

Возможность реализации метода определяется параметрами контролируемой АП, которые влияют на конструктивные параметры вспомогательных элементов измерительной ветви интерферометра.

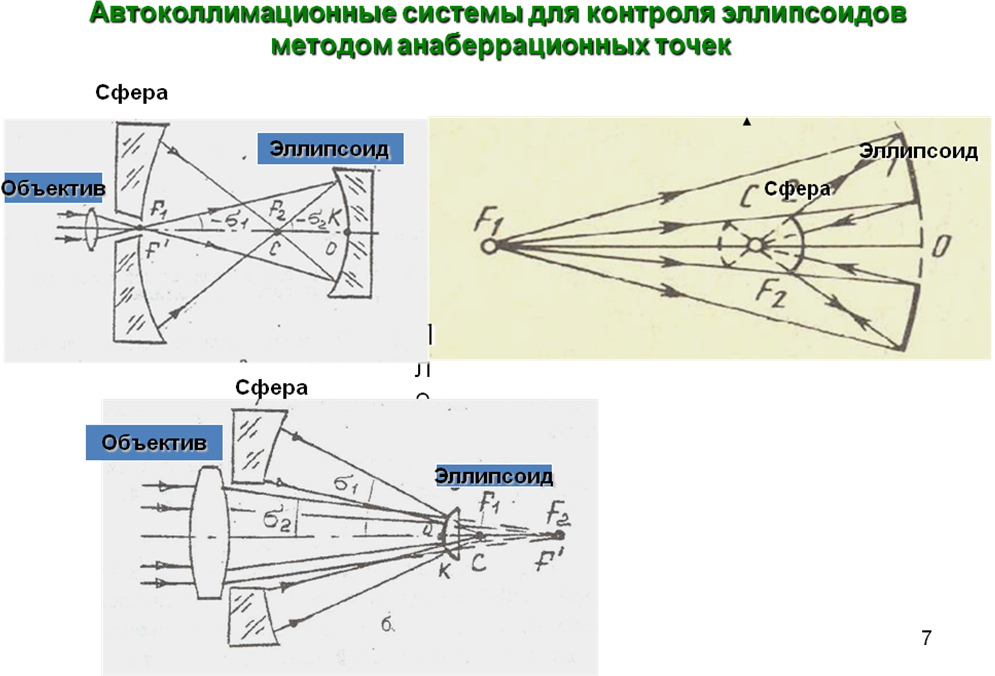
В схеме контроля вогнутых эллипсоидов (рис. а) центр кривизны (точка С)

вспомогательного зеркала совмещен с фокусом F2 ,а вершину его поверхности

целесообразно совместить с другим фокусом эллипсоида F1 . Очевидно, что значения радиуса кривизны и диаметра вспомогательного зеркала здесь определяют по формулам: 𝑟з = 𝐹1𝐹2 и 𝐷з = 2𝑟з sin 𝜎2; Толщина dв воздушного промежутка между эллипсоидом и

вспомогательным зеркалом, а также удаление s фокуса объектива 5 равны отрезку OF1.

Диаметр неконтролируемой зоны эллипсоида рассчитывают по формуле 𝐷н =

𝐷отв ∙ 𝑂𝐹2⁄𝐹1𝐹2. Очевидным недостатком такой схемы можно считать то, что

вспомогательное зеркало здесь имеет строго индивидуальное назначение.

В схеме контроля выпуклых эллипсоидов (рис. б) требуется, чтобы на эллипсоид падал сходящийся гомоцентрический пучок лучей. Это обстоятельство накладывает ограничения на диапазон параметров контролируемых в такой схеме эллипсоидов. Здесь безаберрационный фокусирующий объектив 5 должен располагаться левее вспомогательного зеркала . Это приводит к тому, что отверстие в зеркале и диаметр фокусирующего объектива должны быть больше, чем диаметр измеряемой детали. Здесь, так же как в случае с выпуклым параболоидом, необходимо задаться некоторым значением расстояния dв между вершинами сферического зеркала и эллипсоида. Тогда значения радиуса кривизны и диаметра вспомогательного зеркала будут определяться

соотношениями: 𝑟з = 𝑑в + 𝑂𝐹' и 𝐷з = 2𝑟з sin 𝜎'. Диаметр отверстия на зеркале находят по формуле: 𝐷отв = 2(𝑟з + 𝐹'𝐹0)𝑡𝑔𝜎0 ; Диаметр неконтролируемой зоны на эллипсоиде: 𝐷н = 𝐷отв ∙ 𝑂𝐹'⁄𝑟з ; Из этого выражения очевидно, что по мере увеличения расстояния dв диаметр неконтролируемой зоны уменьшается, но, вместе с тем, увеличиваются значения радиуса кривизны и диаметра вспомогательного зеркала. Удаление s фокуса объектива здесь равно OF2. Недостаток схемы (рис. б) в том, что вспомогательное зеркало здесь

является элементом индивидуального назначения: его параметры жестко связаны с параметрами измеряемого эллипсоида. Кроме того, то обстоятельство, что фокусирующий объектив должен иметь больший диаметр, чем у эллипсоида, накладывает ограничения на параметры контролируемых эллипсоидов.

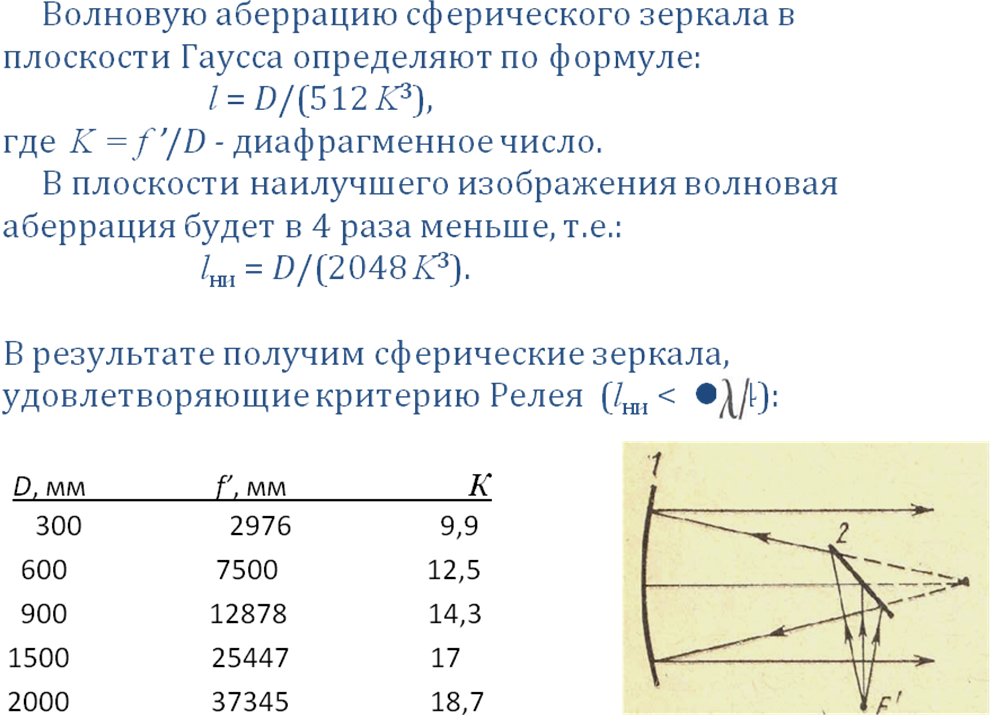
Для обеспечения высокой точности измерений необходимо, чтобы измерительная ветвь не вносила никаких искажений в рабочий волновой фронт, кроме тех, которые обусловлены погрешностями формы измеряемой поверхности. Фокусирующий объектив должен быть идеально исправлен на сферическую аберрацию, т.е. по современным критериям их остаточная волновая аберрация не должна превышать одной сотой длины волны. Форма поверхностей вспомогательных зеркал также должна быть идеальной. В тех случаях,

когда это невыполнимо, поверхности вспомогательных зеркал должны тщательно

аттестовываться. Кроме того, необходимо, чтобы методика юстировки измерительной ветви обеспечивала правильное взаимное расположение всех ее элементов.

5. Теоретические основы компенсационного метода контроля формы асферических поверхностей. Известные конструкции компенсаторов аберраций нормалей к асферическим поверхностям, их достоинства и недостатки. Анализ факторов, влияющих на точность измерений с использованием компенсационного метода.

В двухлучевых интерферометрах для контроля формы оптических

поверхностей опорный волновой фронт обычно имеет регулярную

форму: он либо плоский, либо сферический. Для создания опорного

фронта применяют плоские и сферические поверхности, которые называют эталонными. В большинстве случаев опорный волновой фронт получается путем отражения от эталонной поверхности интерферометра.

При контроле любой оптической поверхности рабочий волновой фронт

отражается от этой поверхности и приобретает искажения, связанные с погрешностями формы поверхности. При этом в большинстве случаев обеспечивают нормальное падение лучей рабочего пучка на контролируемую поверхность: тогда происходит автоколлимация рабочего пучка. На плоскую контролируемую поверхность направляют коллимированный пучок лучей, а на сферическую – гомоцентрический.

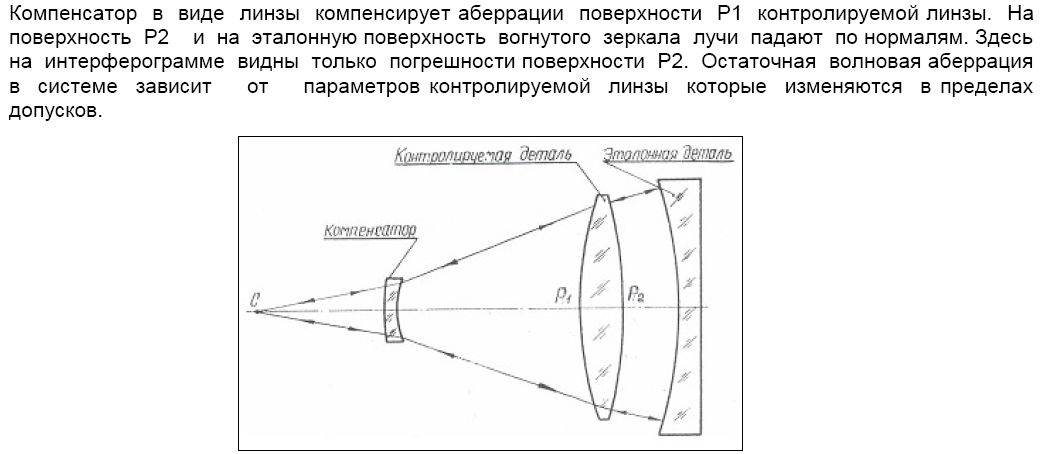
Иначе дело обстоит с АП, так как на них необходимо направлять негомоцентрические пучки, лучи которых являются нормалями к АП. Так нормали к АП характеризуются большими аберрациями, то для создания негомоцентрических пучков нужной конфигурации применяют специальные оптические элементы, называемые компенсаторами аберраций нормалей. Компенсаторы в основном являются элементами индивидуального назначения, так как их рассчитывают персонально под каждую контролируемую АП.

Разрабатывая компенсатор для контроля определенной АП оптик создает исправленную на сферическую аберрацию оптическую систему, состоящую из контролируемой АП и некоторого оптического элемента (компенсатора). Если требования к соблюдению формы АП высоки, то допустимые остаточные аберрации этой системы не должны превышать сотых долей длины волны излучения, используемого в интерферометре.

Метод контроля АП, основанный на использовании компенсаторов, принято называть компенсационным. Параметры компенсационной системы рассчитывают так, чтобы любой вошедший в компенсатор луч регулярного пучка падал нормально на контролируемую АП, а затем после отражения повторял свой путь в обратном направлении.

Конструктивные параметры компенсатора зависят от аберрационных характеристик контролируемой АП. Конструкции известных компенсаторов весьма многообразны, но основные требования, которые необходимо соблюдать при разработке новых компенсационных систем следующие: