Раздел 5

1) Пусть в прямоугольной декартовой системе координат { } M₀=(x₀,y₀) – центр окружности γ.

₁₎ - радиусу окружности, т.е. .

(1) – уравнение окружности с центром M₀=(x₀,y₀) и радиусом R.

2) Выберем систему координат такую что Ox проходит через F₁ и F₂, проходит через середину отрезка F₁F₂. Тогда F₁(-c,0), F₂(c,0).

1. Пусть - произвольная точка эллипса

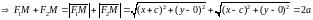
так как

| :

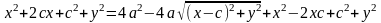
. Обозначим .

(3) – каноническое уравнение эллипса.

Раздел 6:

3)

4. Теорема 1. (Основная теорема о многочленах). Любой многочлен положительной степени над полем F допускает представление в виде произведения неприводимых над F многочленов, причем такое представление единственно с точностью до порядка следования множителей и ассоциированности.

Доказательство. 1) Существование. Пусть f(x) F(x) и deg f(x)=n>0. Доказательство проведем методом математической индукции по параметру n.

1. Пусть n=1 f(x) неприводим над F => f(x)=f(x) - искомое представление.

2. Допустим, что утверждение верно для любого многочлена положительной степени < n над полем F.

3. Докажем утверждение для многочлена f(x). Если f(x) неприводим над F, то f(x)=f(x) –искомое представление. Пусть f(x) приводим над F f(x)=f₁(x) , где f₁(x),f₂(x) F[x] и 0 < deg f_i < n, i= f₁(x) = p₁(x)· p₂(x) · …·p_r(x) и f₂(x)=q₁(x) ·…·q_s(x) – представление и в виде произведения неприводимых над многочленов f = f_{1 ·} f₂ = p₁·_…·p_r· q₁·_…·q_s – искомое представление.

Из 1-3 по методу математической индукции утверждение верно для любого n N.

2) Единственность. Пусть f(x)=p₁(x)·_…·p_r(x) и f(x)=q₁(x)·_… ·q_s(x) – требуемые представления (1). Так как r,s N, то либо r s, либо r s. Пусть, например, r s. Так как левая часть (1) делится на p₁ (q₁·_…·q_s) p₁ по лемме 4 хотя бы один из множителей делится на p₁. Так как множители можем менять местами, то будем считать, что q₁ p₁ по лемме 2 q₁~q₂ и по замечанию 3 q₁=p₁·a₀ , где a₀ F^# => p₁·_…·p_r=a₀ · p₁· q₂·_…·q_s, (2). Так как левая часть (2) делится на р₂, то как и выше, получим р₂~q₂ и р₂=q₂·b₀ , где b₀ F^#, причем (3) и т.д., через конечное число шагов получим 1=а₀· ₀·_…·q_r+1·_…·q_s (4). Допустим, что r<s => 1 q_r+1 => deg q_r+1=0 => противоречие => r=s. Таким образом, представление многочлена f(x) в виде требуемого произведения определяется однозначно с точностью до порядка следования множителей и ассоциированности. Теорема доказана.

4. Теорема 16. Пусть ∈ Z[x], , - несократимая рациональная дробь. Если - корень f(x), то , .

Доказательство. Пусть - корень f(x) 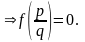Пусть . По теореме Безу f(x)=(x-c)q(x)+f(c) (1). Пусть q(x)=

.

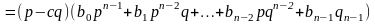
Покажем, что . Допустим, что (q, p-cq)=d > 1

- противоречие . Теорема доказана.

Следствие 16.1. Пусть f(x) Z[x] , - несократимая рациональная дробь. Если - корень f(x), то .

2) Теорема 8. Пусть F – поле, f(x), g(x) F[x], g(x) 0. Тогда существуют единственные многочлены q(x), r(x) F[x] такие, что f(x)=g(x)·q(x)+r(x), причем degr(x)<degg(x).

Доказательство. 1.

Существование. Если f(x)=0 q(x)=0, r(x)=0, причем degr(x)= − < deg g(x) 0. Если deg f(x)<deg g(x) q(x)=0, r(x)=f(x), причем degr(x)=degf(x)<deg g(x).

Пусть f(x) 0 и deg f(x) deg g(x). Пусть f(x)=a_o+a₁x+…+a_nxⁿ, g(x)=b_o+b₁x+…+b_mx^m n m. Доказательство проведем методом математической индукции по параметру n.

1) Пусть n=0 f(x)=a_o g(x)=b_o , причем deg r(x)= − <0=deg g(x).

2) Предположим, что утверждение верно для любого многочлена степени, меньшей n.

3) Докажем утверждение для многочлена степени n.

f(x)=a_o+…+a_nxⁿ

g(x)=b_o+…+b_mx^m ∙b_m^-1∙a_nx^n-m

h(x)=f(x)-g(x)∙b_m^-1∙a_nx^n-m=a_o+…+(a_nxⁿ-b_mb_m^-1a_nx^mx^n-m) h(x) - многочлен степени, меньшей n q₁(x), r₁(x) F[x]: h(x)=g(x)∙q₁(x)+r₁(x), где deg r₁(x)<deg g(x)

f(x)-g(x)=g(x)∙q₁(x)+r₁(x) , причем deg r(x)<deg g(x).

Из 1)-3) по методу математической индукции следует, что утверждение верно .

2. Единственность. Пусть f(x)=g(x)∙q₁(x)+r₁(x) (1) и f(x)=g(x)∙q₂(x)+r₂(x) (2). Покажем, что q₁=q₂, r₁=r₂. Вычтем из равенства (1) равенство (2): 0=g(x)(q₁-q₂)+(r₁-r₂) r₂-r₁=g(x)(q₁-q₂) (3).

Допустим, что q₁-q₂ 0. Согласно теореме 3, F[x] - область целостности. Поэтому в F[x] нет делителей нуля и из (3) следует, что . Тогда, с одной стороны,

deg(r₂-r₁) 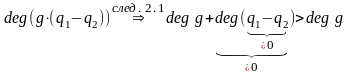, т.е. .

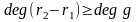С другой стороны, , т.е. deg(r₂-r₁)<deg g. Противоречие. Следовательно, . Теорема доказана.