4. Теорема (критерий ортогональности векторов).

Пусть Тогда

Доказательство.

а) Необходимость(). Пусть

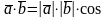
=0.

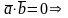
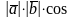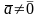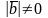а) Достаточность(). Пусть =0. Так как и , то и cos =0 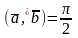(поскольку Î [0, π]) .

Раздел №4.

1.1)Параметрические уравнения прямой по точке и направляющему вектору.

1. Пусть М(x,y) – произвольная точка, лежащая на прямой . Покажем, что ee координаты удовлетворяют уравнению (2).

Так как М(x,y)∈ l и М₀(x₀,y₀)∈ l , то . Тогда . Следовательно, 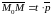для некоторого 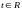. В координатной форме:

(2) параметрические уравнения прямой по точке 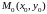и направляющему вектору 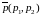. t – параметр.

1.2)Каноническое уравнение прямой по точке и направляющему вектору.

Выразим из обоих уравнений (2) параметр t.

каноническое уравнение прямой по точке и направляющему вектору .

1.3) Уравнение прямой, проходящей через 2 точки

Пусть на прямой l заданы точки и . Тогда вектор является направляющим вектором для .

Согласно (3), уравнение по точке и направляющему вектору имеет вид

– уравнение прямой, проходящей через точки M₁(x₁,y₁) и M₂(x₂,y₂)

1.4) Уравнение прямой в отрезках на осях

Пусть прямая проходит через точки А(а, 0) и В(0, b).

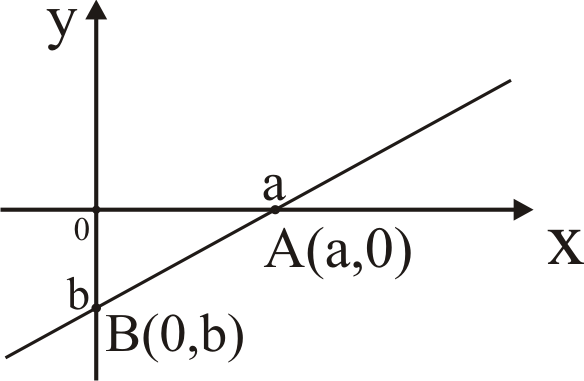
Согласно (4), её уравнение имеет вид:

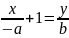; ; ; отсюда

(5) - уравнение прямой, отсекающей на координатных осях отрезки a и b соответственно.

1.5) Общее уравнение прямой

Теорема 1. В аффинной системе координат всякое уравнение первой степени

Ах+Ву+С=0, где А²+В² 0 (7)

задает прямую с направляющим вектором .

Обратно, любая прямая на плоскости имеет уравнение вида (7) – общее уравнение прямой.

Доказательство: 1) Пусть в аффинной системе координат дано уравнение Ах+Ву+С=0, . Покажем, что все точки, координаты которых удовлетворяют (7), лежат на одной прямой с направляющим вектором

Пусть - фиксированная точка, координаты которой удовлетворяют (7), а - любая другая точка, удовлетворяющая (7), тогда

Если A0 и B0, то (*). Получаем, что координаты точки удовлетворяют уравнению (*), которое является уравнением прямой вида (3) по точке и направляющему вектору . Таким образом, все точки, удовлетворяющие уравнению (7), лежат на прямой (*).

Если А=0, то By+C=0;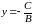 (**) - уравнение прямой, параллельной оси Оx.

Если В=0, то Ax+C=0; (***) - уравнение прямой параллельной оси Оy.

Таким образом, в любом случае все точки , удовлетворяющие уравнению (7) лежат на одной прямой на плоскости.

2) Пусть прямая на плоскости проходит через точку с направляющим вектором . Покажем, что её уравнение можно привести к виду (7).

Если A0 и B0, согласно (3), уравнение : 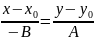. Умножим обе части уравнения на АВ:

.

Обозначив –Ax₀–By₀=C, получим, что прямая l имеет уравнение вида - уравнение вида (7)

Если A=0 получаем согласно (2), уравнение l: 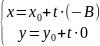, откуда при t∈ℝ получаем x∈ℝ a у=у₀. Таким образом, уравнение данной прямой приводится к виду у-у₀=0 – уравнение вида (7) где А=0, В=1, С=-y₀

Теорема доказана.

2)Параметрические уравнения плоскости

Пусть - направляющие векторы плоскости , ∦ . Отложим и от точки .

1. Покажем, что , ее координаты удовлетворяют уравнениям (1). Поскольку M₀∈, M∈, тогда лежит в плоскости . Отложим векторы и от точки M₀, тогда , , 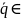∦ . Следовательно и образуют на плоскости  аффинную систему координат. Тогда вектор разлагается по векторам и : для некоторых u, v∈ℝ. Запишем это равенство в координатной форме:

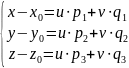
откуда (1) - параметрические уравнения плоскости по точке и направляющим векторам , u, v∈ℝ параметры.

3.1) Уравнение прямой в пространстве по точке и направляющему вектору

Пусть в аффинной системе координат , и .

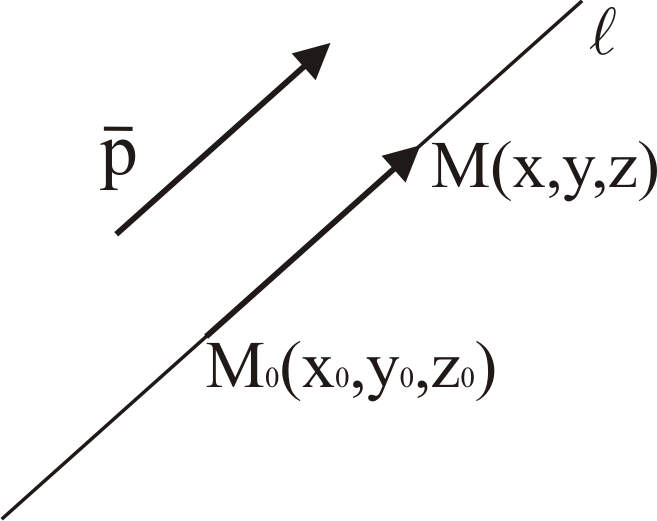
Заметим, что для некоторого t∈ℝ 

t ∈ℝ (1) - параметрические уравнения прямой в пространстве по точке и направляющему вектору .

3.2)Выразим параметр t из каждого уравнения (1)

- канонические уравнения прямой в пространстве по точке и направляющему вектору .

3.3)Уравнение прямой в пространстве по двум точкам.

Пусть в аффинной системе координат заданы координаты двух точек на прямой . Запишем, согласно (2) канонические уравнения прямой по точке и направляющему вектору .

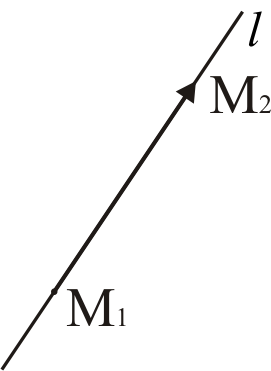
- уравнения прямой в пространстве, проходящей через две точки .
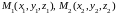