
- •Доказательство теорем.
- •- Подпространство .
- •2. Свойства. Пусть V – евклидово пространство. Тогда
- •4. Свойства эрмитова произведения. , , V, ℂ
- •5. Свойства длины вектора: V
- •4. Теорема (критерий ортогональности векторов).
- •1.3) Уравнение прямой, проходящей через 2 точки
- •1.4) Уравнение прямой в отрезках на осях
- •1.5) Общее уравнение прямой
- •Раздел 5
- •Раздел 6:
2. Свойства. Пусть V – евклидово пространство. Тогда
10. , , V ( + ) = +
Доказательство.
( + ) = ( + ) = + = +
20.
 ℝ,
,
V
(λ
)
= λ (
)
ℝ,
,
V
(λ
)
= λ (
)
Доказательство.
(λ ) = (λ ) = λ( ) = λ ( )
30.
V

= (0
)
=
0(
)
= 0.
= (0
)
=
0(
)
= 0.
Доказательство. Следует из леммы 1.
Лемма1. Пусть V – вещественное пространство со скалярным умножением. Тогда = =0 V .
Доказательство. = + ( + ) = + . = + 0. Тогда + = + 0. По закону сокращения получим = 0. ЧТД.
3. Теорема . Пусть V – комплексное n-мерное векторное пространство. Тогда на V существует эрмитово произведение.
Доказательство. Т.к. V – n-мерное пространство, то в V существует базис, состоящий из n векторов.
Пусть
 базис V. Тогда
базис V. Тогда

,
V
,
V
 ,
,

 .
Зададим отображение V
Vℂ
по правилу
=
.
.
Зададим отображение V
Vℂ
по правилу
=
.
Покажем, что оно является эрмитовым произведением.
а) С учетом свойств
комплексно-сопряженных чисел,
 получим
получим
=
 =
=
 =
=
 =
=
 =
=

=
=
б) Пусть

V . Тогда (
+
)
=
V . Тогда (
+
)
=
 =
=
 +
+
 =
+
=
+
в) ℂ :
(λ
)
=
 =
=
 =
=
 = λ(
)
= λ(
)
г)
=
 =
=
 =
=
 ,
где
,
где
 ℝ,
ℝ,
 ,
причем
,
причем
 =0 ,
=0 ,


=
=
4. Свойства эрмитова произведения. , , V, ℂ
10. ( + ) = +
Доказательство.
(
+
)
=
 =
=
 =
+
ч.т.д
=
+
ч.т.д
20.
(λ
)
=

Доказательство.
(λ
)
= =
ч.т.д
=
ч.т.д
30. = = 0.
Доказательство.
= ( + ) = +
= + 0 + = + 0 = 0. ч.т.д
5. Свойства длины вектора: V
10. |
|
 0, причем |
|
= 0
=
0, причем |
|
= 0
=
Доказательство.
Евклидово пространство:
|
|
=
 ≥0, т.к.
≥0, т.к.
 по определению 1, причем
|
|
= 0
по определению 1, причем
|
|
= 0
 =0
=
.
=0
=
.
Унитарное пространство: | | = 0, т.к. по определению 5, причем | | = 0 =0 = .
20. Если
 ℂ, то |λ
|
= |λ||
|
ℂ, то |λ
|
= |λ||
|
Доказательство.
|λ
|
=
 ,
где
,
где

6. Теорема . Пусть V – n–мерное евклидово пространство, или унитарное пространство. Тогда любая система ненулевых ортогональных векторов из V линейно – независима.
Доказательство.
Пусть
 (1) – ортогональная система ненулевых
векторов из V. Покажем,
что (1) линейно независима.
(1) – ортогональная система ненулевых
векторов из V. Покажем,
что (1) линейно независима.
Рассмотрим линейную
комбинацию
 (2).
(2).
Умножим скалярно обе
части неравенства (2) на вектор
 ,
,
 :
:
 .
.
По свойству билинейности получим:

По условию, система
(1) ортогональна. Тогда
 .
Т.к.
.
Т.к.
 ,
значит
,
значит
 =0
=0
 .
.
Т.о., система (1) линейно – независима. ч.т.д.
7. Теорема . Пусть V – n–мерное евклидово или унитарное пространство. Тогда любая ортогональная система ненулевых векторов из V может быть дополнена до ортогонального базиса.
Доказательство. Пусть (1) - ортогональная система не нулевых векторов из V. По теореме 5 , система (1) линейно независима. Значит, систему (1) можно дополнить до базиса V.
Пусть
 (2) – базис векторного пространства V.
Подправим базис (2) так, чтобы из него
получился ортогональный базис. Подправим
вектор
(2) – базис векторного пространства V.
Подправим базис (2) так, чтобы из него
получился ортогональный базис. Подправим
вектор
 следующим образом:
следующим образом:
заменим
вектором
 ,
таким, что
ортогонален векторам
:
,
таким, что
ортогонален векторам
:
=
 (3), причем будем полагать, что
выбраны так, что вектор
ортогонален всем предыдущим векторам
системы (2).
(3), причем будем полагать, что
выбраны так, что вектор
ортогонален всем предыдущим векторам
системы (2).
Найдем коэффициенты равенства (3). Для этого умножим скалярно обе части равенства (3) на :
=

=
= ,
,
 ,
(4)
,
(4)
Формула (4) позволяет
найти вектор
,
который ортогонален всем векторам
,
т.е.
,
- ортогональные векторы.Отметим, что
согласно теореме 2,
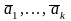 ,
линейно независима. Значит,
.
Т.о.
,
- ортогональная система ненулевых
векторов.
,
линейно независима. Значит,
.
Т.о.
,
- ортогональная система ненулевых
векторов.
Применим этот процесс
– процесс ортогонализации – к вектору
 ,
т.е. заменим его вектором
,
т.е. заменим его вектором
 ,
который будет ортогонален векторам
,
.
,
который будет ортогонален векторам
,
.
Продолжая этот процесс,
через конечное число шагов получим
,
,…, ортогональный базис V.
ч.т.д.
ортогональный базис V.
ч.т.д.
8.
Теорема . V
– n- мерное евклидово
пространство,
 …
…
 - ортонормированный базис V.
Тогда скалярное умножение относительно
этого базиса является стандартным, т.е
если
,
V,
=
- ортонормированный базис V.
Тогда скалярное умножение относительно
этого базиса является стандартным, т.е
если
,
V,
=
 ,
=
,
=
 ,
причем
,
причем
 =
=
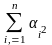
Доказательство.
Пусть
,
V,
=
,
=
=
= ( +
+ )
(
)
(
 )
=
)
=
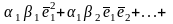
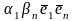 +
+
 +
+

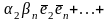
 +
+
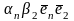 +…+
+…+
 =
=

=
=
 =
=
=
=
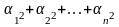
Раздел №3.
1. Теорема . Множество всех векторов в пространстве образует абелеву группу относительно операции сложения векторов.
Доказательство. Множество всех векторов замкнуто относительно операции сложения, так как сумма векторов по определению 8 является вектором.
Ассоциативность:

Пусть
 ,
,
 ,
, .
По определению 8,
.
По определению 8,

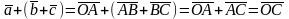 ,
ассоциативность доказана.
,
ассоциативность доказана.
2. Существует нейтральный
элемент
 (см. опр.6), такой что
(см. опр.6), такой что



3.
существует противоположный вектор (см.
опр.7)
 ,
,
такой что


4. Коммутативность операции сложения
,
 (1) см рис. 6.
(1) см рис. 6.

Отложим теперь
 .
Тогда OABC – параллелограмм.
Отсюда
.
Тогда OABC – параллелограмм.
Отсюда
 .
.
Тогда
 (2). Из (1) и (2) следует
(2). Из (1) и (2) следует
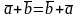 .
Теорема доказана.
.
Теорема доказана.
2.
Теорема . Пусть на плоскости
даны два неколлинеарных вектора
 и
и
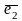 .
Любой вектор
на
плоскости можно представить в виде
.
Любой вектор
на
плоскости можно представить в виде
 ,
где
,
где
 Î
ℝ, причем такое
представление единственно.
Î
ℝ, причем такое
представление единственно.
Доказательство. I
. Существование. Если
 или
или
 ,
то
||
,
что противоречит с условием, следовательно,
,
то
||
,
что противоречит с условием, следовательно,
 и
и
 .
.
Если
||
,
то
 ,
для некоторого
Î
ℝ (см. опр.9) и
искомое разложение вектора
,
для некоторого
Î
ℝ (см. опр.9) и
искомое разложение вектора
 .
.
Если
||
аналогично существует
 Î
ℝ:
Î
ℝ:
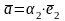 ,
т.е.
,
т.е.
 .
.
Если ∦ и ∦ , отложим , , от одной точки O. Пусть .

Проведем прямые AP
и AQ, такие что
||
AQ и
||
AP Тогда
 ||
,
следовательно,
=
||
,
следовательно,
=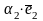 ,
,
 ||
,
следовательно,
=
||
,
следовательно,
= для некоторых
Î
ℝ.
для некоторых
Î
ℝ.

 -
искомое разложение.
-
искомое разложение.
II.
Единственность. Пусть
 ,
где, например,
,
где, например,
 ,
тогда, вычитая почленно, получим
,
тогда, вычитая почленно, получим
 ,
где
,
где
 .
Далее,
.
Далее,
 ,
,
 | :
| :
 ,
откуда следует по опр.9, что
||
,
противоречие условию. Теорема доказана.
,
откуда следует по опр.9, что
||
,
противоречие условию. Теорема доказана.
Аналогично доказывается
3.
Теорема. Пусть в аффинной
системе координат {O,
,
, }
векторы заданы своими координатами
}
векторы заданы своими координатами
 ,
,
 ,
тогда умножение вектора на скаляр и
сложение векторов производится
покоординатно, т.е.
,
тогда умножение вектора на скаляр и
сложение векторов производится
покоординатно, т.е.
1.

2.
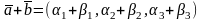
Доказательство.
1. Так как
 ,
то
,
то
 (т.2)
(т.2)
 ,
т.е.
,
т.е.
2. Так как
 ,
то
,
то
 +
+
 =(т.1,
т.2)=
=(т.1,
т.2)= ,
то есть
,
то есть
