
- •Доказательство теорем.
- •- Подпространство .
- •2. Свойства. Пусть V – евклидово пространство. Тогда
- •4. Свойства эрмитова произведения. , , V, ℂ
- •5. Свойства длины вектора: V
- •4. Теорема (критерий ортогональности векторов).
- •1.3) Уравнение прямой, проходящей через 2 точки
- •1.4) Уравнение прямой в отрезках на осях
- •1.5) Общее уравнение прямой
- •Раздел 5
- •Раздел 6:
Доказательство теорем.
Раздел №1.
1.
Теорема. Пусть
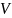 и
и
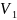 – векторные пространства над полем
– векторные пространства над полем
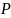 ,
,
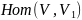 .
Тогда
.
Тогда
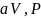 :
:
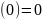 .
. .
. .
.
Доказательство.
Так как
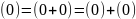 ,
то
,
то
 .
.Так как
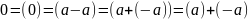 ,
то
,
то

Методом математической индукции:
Для
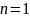 :
:
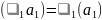 - верно.
- верно.Предположим, что для
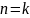 :
.
:
.Докажем, что для
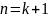 :
.
Действительно,
:
.
Действительно,
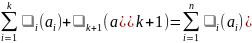 .
.
2. Теорема.
Пусть
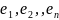 – базис векторного пространства
– базис векторного пространства
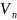 над полем
.
над полем
.
 – векторное пространство над полем
.
Если
– векторное пространство над полем
.
Если
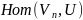 ,
то
,
то
 - однозначно определяется заданием
образов базисных векторов.
- однозначно определяется заданием
образов базисных векторов.
Доказательство.
Покажем, что
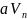
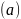 – однозначно определено образами
– однозначно определено образами
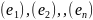 .
Пусть
,
тогда
.
Пусть
,
тогда
 - единственное разложение вектора
- единственное разложение вектора
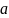 по базису
.
Следовательно,
по базису
.
Следовательно,
 - единственное представление вектора
относительно векторов
- единственное представление вектора
относительно векторов
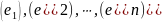 .
.Покажем, что отображение однозначно определяется заданием образов базисных векторов. Допустим, что , по правилу
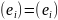 – некоторое другое линейное отображение.
Тогда
– некоторое другое линейное отображение.
Тогда
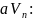
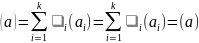 .
Следовательно,
.
.
Следовательно,
.
3.
Теорема. Пусть
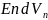 ,
– базис
,
,
– базис
,
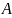 – матрица линейного оператора
относительно базиса. Если
– матрица линейного оператора
относительно базиса. Если
 ,
то
,
то
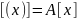 .
.
Доказательство.
Пусть
,
тогда
 ,
следовательно,
,
следовательно,
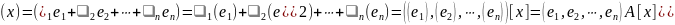 .
Из
.
Из
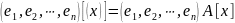 ,
следует, что
,
следует, что
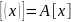 .
.
4.
Теорема. Пусть
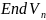 ,
–
,
–
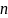 -мерное
векторное пространство над полем
.
Тогда:
-мерное
векторное пространство над полем
.
Тогда:
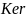 - подпространство
.
- подпространство
.- Подпространство .
Доказательство. Непосредственной проверкой критерия подпространства.
Покажем, что - подпространство :
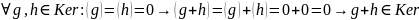 .
.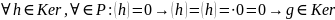 .
.
Покажем, что - подпространство .
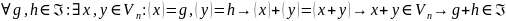 .
. .
.
5.
Теорема. Пусть
и
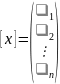 - координатный вектор столбец вектора
- координатный вектор столбец вектора
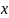 в базисе (1),
в базисе (1),
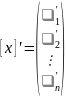 - координатный вектор столбец вектора
в базисе (2).
- координатный вектор столбец вектора
в базисе (2).
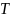 – матрица перехода от базиса (1) к базису
(2).
– матрица перехода от базиса (1) к базису
(2).
Тогда
 или
или
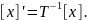
Доказательство.
Так как
в базисе (1), то
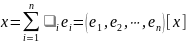 .
Аналогично,
.
Аналогично,
 .
Следовательно,
.
Следовательно,
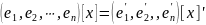 .
Так как
– матрица перехода от базиса (1) к базису
(2), то
.
Так как
– матрица перехода от базиса (1) к базису
(2), то
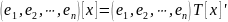 .
.
Таким образом, получаем что или
6.
Теорема. Пусть
,
–
-мерное
векторное пространство над полем
.
– матрица линейного оператора
в базисе (1),
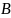 - матрица линейного оператора
в базисе (2). Если
– матрица перехода от базиса (1) к базису
(2), то
- матрица линейного оператора
в базисе (2). Если
– матрица перехода от базиса (1) к базису
(2), то
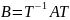 .
.
Доказательство.
Так как
– матрица линейного оператора
в базисе (1), то
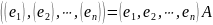 .
Аналогично, для матрицы
:
.
Аналогично, для матрицы
:
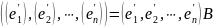 .
.
Так как
– матрица перехода от базиса (1) к базису
(2), то
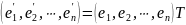 .
И
.
И

7. Пусть Vn
– n-мерное векторное
пространство над полем P,
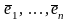 (1) – базис Vn,
(1) – базис Vn,
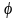 - линейный оператор векторного пространства
Vn.
Найдём все собственные векторы и все
собственные значения линейного оператора
.
Пусть
- линейный оператор векторного пространства
Vn.
Найдём все собственные векторы и все
собственные значения линейного оператора
.
Пусть
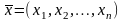 – собственный вектор линейного оператора
.
Найдём
– собственный вектор линейного оператора
.
Найдём
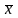 .
.
По
определению 1
 ,
где λ
,
где λ P
P
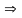
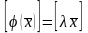 . С другой стороны,
. С другой стороны,
 .
Поэтому
.
Поэтому
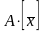 =
= ,
т.е.
,
т.е.
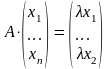 .
.
Пусть
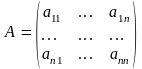 - матрица линейного оператора
в базисе (1)
- матрица линейного оператора
в базисе (1)
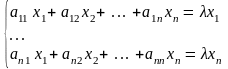
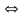
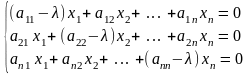 (2).
(2).
Раздел №2.
1. Теорема 1. Пусть V – n-мерное вещественное векторное пространство. Тогда на V существует ненулевое скалярное умножение.
Доказательство. Т.к. V – n-мерное пространство, то в V существует базис, состоящий из n векторов.
Пусть
 ..,
..,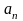 - базис V. Тогда
- базис V. Тогда 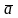 ,
,
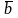 V
V
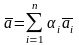 ,
,
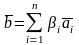 .
.
Зададим отображение
: V
W ℝ по правилу
,
V
W
((
,
))
=
=
ℝ по правилу
,
V
W
((
,
))
=
=
 .
.
Покажем, что является скалярным умножением.
а)
,
V
:
=
=
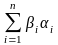 =
=
б) Пусть
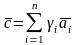 V.
Тогда (
+
)
V.
Тогда (
+
)
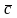 =
=
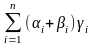 =
=
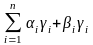 =
=
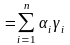 +
+
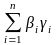 =
+
.
=
+
.
в) 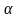
ℝ :
(
)
=
=
ℝ :
(
)
=
=
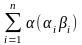 =
=
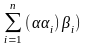 =
(
)
.
=
(
)
.
г)
=
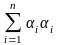 =
=
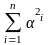
0, причем
=
0
0, причем
=
0
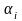 = 0, i =
= 0, i =
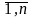 .
.
Покажем, что оно не нулевое.
 =
1
+
0
=
1
+
0
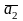 +…+
0
+…+
0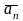
= 1 0
Ǝ хотя бы 1 вектор,
для которого скалярное произведение
не нулевое.
= 1 0
Ǝ хотя бы 1 вектор,
для которого скалярное произведение
не нулевое.
