26. Криптосистема Эль-Гамаля.

Пусть иемются абоненты А,Б,С,…, которые хотят передавать друг другу зашифрованные сообщения, не имея никаких защищенных каналов связи. Фактически здесь используется схема Деффи-Хелмана, чтобы сформировать общий секретный ключ для 2-х абонентов передающих друг другу сообщение, и затем сообщение шифруется путем умножения его на этот ключ. Для каждого следующего сообщения секретный ключ вычисляется заново.

Описание системы.

Генерация ключей

Для всей группы абонентов выбираются некоторое большое число p и число g, такие , что различные степени g суть различные числа по модулю p. Числа p и g передаются абонентам в открытом виде (они могут использоваться всеми абонентами линиями). Затем каждый абонент группы выбирает свое секретное число 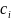, 1< 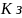<p-1, и вычисляет соответствующее ему открытое число

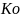
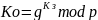
шифрование

А формирует случайное число c, 1≤c≤p-2, вычисляет числа

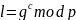
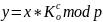
И передает пару числе (l,y) l-вспомогательный параметр

расшифрование

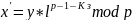
27.Криптосистема Шамира.

Криптосистема организовывать обмен секретными сообщениями по открытой линии связи для лиц, которые не имеют никаких защищенных каналов и секретных ключей и, возможно не видели друг друга.

Описание системы.

Пусть есть 2 абонента А и Б, соединенные линией связи. А хочет передать сообщение m абоненту Б так, что бы никто не узнал его содержание. А выбирает случайное большое число p и открыто его передает Б. Абонент А и Б по одному и тоже алгоритму формируют 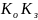такие, что

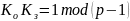
Эти числа держится в секрете и передавать не будет.

После этого А передает свое сообщение m, используя 3-хступенчатый протокол. Если x<p, то сообщение x передается сразу, если x>p, то сообщение разбивается на блоки.

Описание протокола:

Шаг 1. А вычисляет число

,

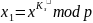и пересылает 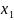к Б

Шаг 2. Б получив , вычисляет число

,

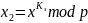И передает 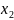к А.

Шаг 3. А вычисляет число

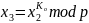
И передает его Б.

Шаг 4. Б получив число 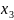, вычисляет число

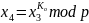.=x

Недостаток: необходимо 3 раза передавать инф.

Особенность: ключи формируются и никуда не передаются

28.Криптосистема rsa.

Основан на задаче факторизации чисел ( разложение в произведение простых множителей)

Генерация ключей:

Каждый абонент выбирает случайно 2 больших простых числа p и q. Затем он вычисляет число

n=p*q

(Число n является открытой информацией, доступной другим абонентам). После этого абонент вычисляет функцию Эйлера φ=(p-1)*(q-1).Выбирает открытый ключ 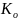< φ, взаимно простое с φ (не имеет общих делителей), и по обощенному алгоритму Евклида находит число c, такое, что

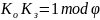(взаимнообратное)

Пара чисел <n, > - откр ключ. 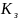- никуда не передается

шифрование

Пусть Алиса хочет передать сообщение x Бобу.

Шаг 1. Проверяется: x<n. Алиса шифрует сообщение по формуле

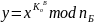
Используя открытые параметры Боба, и пересылает y по открытой линии

Шаг 2. Боб получивший зашифрованное сообщение, вычисляет

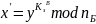
Недостаток: А передает сообщение Б, используя открытую информацию абонента Б (числа и 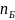). Злоумышленник не может читать сообщения, предназначенные для Б, однако он может передать сообщение к Б от имени А. избежать этого можно, используя более сложные протоколы.