
- •1)Основные понятия криптографии
- •2)Этапы становления криптографии, как науки.
- •3)Понятие криптосистемы. Классификация криптосистем. Основные требования к криптосистеме
- •4)Алгебраическая и вероятностная модели шифра.
- •5) Модели открытых текстов. Характеристики открытых текстов
- •6) Шифры замены: определение, разновидности шифров замены
- •7) Шифры перестановки: определение, разновидности шифров перестановки.
- •8) Симметричная криптосистема. Типы симметричных криптосистем.
- •9) Блочная криптосистема: понятие, принципы построения блочных криптосистем, достоинства и недостатки.
- •10) Режимы применения блочных криптосистем.
- •11) Криптосистема des.
- •Криптосистема гост 28147-89
- •14)Методы усложнения блочных симметричных криптосистем.
- •15)Поточная криптосистема: понятие, принципы построения поточных криптосистем, достоинства и недостатки.
- •16) Типы поточных криптосистем (синхронная поточная криптосистема, самосинхронизирующаяся поточная криптосистема).
- •17) Методы криптоанализа симметричных криптосистем: метод полного перебора, частотный метод, метод чтения в колонках, метод «протяжки» вероятного слова.
- •18) Линейный криптоанализ: суть метода линейного криптоанализа, этапы реализации метода.
- •19) Дифференциальный (разностный) криптоанализ: суть метода дифференциального криптоанализа, этапы реализации метода.
- •20)Понятие совершенно стойкой криптосистемы. Теорема Шеннона.
- •21) Теорема о совершенной стойкости шифра Вернама.
- •22) Идеально стойкая криптосистема. Расстояние единственности шифра.
- •23.Понятие практической стойкости криптосистемы.
- •24.Односторонняя функция. Типы используемых односторонних функций.
- •25) Криптосистема с открытым ключом: понятие криптосистемы с открытым ключом, принципы построения, достоинства и недостатки.
- •26. Криптосистема Эль-Гамаля.
- •27.Криптосистема Шамира.
- •28.Криптосистема rsa.
- •29) Криптосистема Рабина.
- •30.Понятие эллиптической кривой. Свойства точек эллиптической кривой. Выбор параметров эллиптической кривой.
- •31.Криптосистема Эль-Гамаля на эллиптической кривой.
- •32.Методы криптоанализа криптосистем с открытым ключом: метод криптоанализа «шаг младенца, шаг великана», метод исчисления порядка.
- •33) Понятие хэш-функции. Требования к хэш-функциям.
- •34.Понятие эцп. Свойства эцп.
- •35. Эцп на базе криптосистемы rsa.
- •36.Эцп на базе Эль-Гамаля.
- •37.Стандарты эцп: гост р.34.10-94. Особенности алгоритма dsa.
- •Область применения
- •38) Понятие криптографического протокола. Типы криптографических протоколов.
- •39) Протоколы управления ключами с использованием симметричных криптосистем (двусторонние и трехсторонние протоколы).
- •40) Протоколы управления ключами с использованием криптосистем с открытым ключом.
- •41) Криптографический генератор: понятие, требования к криптографическим генераторам, классификация криптографических генераторов.
- •42) Комбинированные криптографические генераторы.
- •43) Методы улучшения «элементарных» псевдослучайных последовательностей.
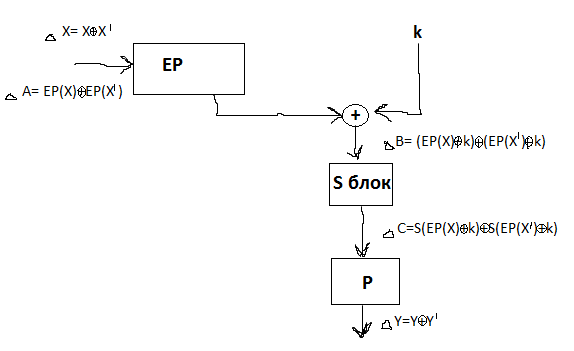
19) Дифференциальный (разностный) криптоанализ: суть метода дифференциального криптоанализа, этапы реализации метода.
Идея метода заключается в анализе процесса изменения несходства пары открытых текстов, имеющих определенные исходные различия в процессе прохождения через циклы шифрования с одним и тем же ключом.
20)Понятие совершенно стойкой криптосистемы. Теорема Шеннона.
Предположим, что имеется конечное число возможных открытых сообщений X={X1,X2,…,Xm}, множество возможных ключей K={k1,k2,k3,…,kl} и множество криптограмм Y={Y1,Y2,Y3,…,Ym}. Задано криптопреобразование Yj=f(Xi,kl}.
Заданы априорные вероятности P(Xi), i=1,m. Это распределение вероятностей известно противнику. После того как противник перехватил криптограмму Yj, j=1,n, он может вычислить по крайней мере апосориорные вероятности различных сообщений P(Xi|Yj).
Криптосистема
называется совершенностойкой, если
P(Xi|Yi)=P(Xi),
i=(1,m),
т.е. перехват криптограммы не дает
криптоаналитику никакой информации.
Открытый текст и криптограмма статистически
независимы. Если система совершенно
стойка, то справедливо равенство
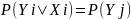


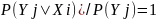
Теорема Шеннона: Если система является совершенностойкой, то оправдано равенство P(Yi|Xi)=P(Yi). Полная вероятность всех ключей, переводящих сообщение Xi в крипторамму Yi равна полной вероятности всех ключей, переводящих сообщение Xk в криптограмму Yi.
21) Теорема о совершенной стойкости шифра Вернама.
Шифр Вернама является совершенно стойкой криптосистемой.
Согласно теореме Шеннона, достаточно доказать:
Имеем:
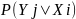
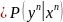 =
=
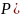


В
этом выражении использовано предположение
о равновероятности ключей. Найдем P(Yj).
По формуле полной вероятности
 Учитывая тот факт, что
Учитывая тот факт, что
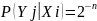 ,
получаем:
,
получаем:
 при
при

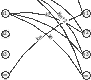
Совершенно стойкие криптосистемы характеризуются следующими св-ми:
каждое открытое сообщение
 связывается с криптограммой
связывается с криптограммой
 только
одной линией;
только
одной линией;
все ключи равновероятны.
Теорема о совершенной стойкости шифра Вернама: шифр Вернами является совершенностойкой криптосистемой.
22) Идеально стойкая криптосистема. Расстояние единственности шифра.
Идеальностойкая
криптосистема- такая система в которой
величины ,![]() N-
длинна криптограммы, H(K|Y) – ненадежность
ключа, H(X|Y)
– ненадежность сообщения.
N-
длинна криптограммы, H(K|Y) – ненадежность
ключа, H(X|Y)
– ненадежность сообщения.
H(K|Y)=- ,
H(X|Y)=-
,
H(X|Y)=-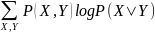 ,
где
,
где
 и
и
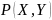 – совместные вероятности,
– совместные вероятности,
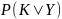 ,
,
 – апосториорные вероятности. Если
ненадежность =0, то это значит, что одно
сообщение имее еденичную вероятность,
а все другие нулевую. Постепенное
убывание ненадежности с ростом N
соответсвует увеличению сведений об
исходном ключе или сообщении. Строго
идеально стойкой КС – это такая КС, в
которой H(K|Y)
остается равной H(K)/(
пример – простая подстановка, примененная
к искусственному языку, в которой все
буквы равновероятные и последовательные
буквы выбираются незавсимо).
– апосториорные вероятности. Если
ненадежность =0, то это значит, что одно
сообщение имее еденичную вероятность,
а все другие нулевую. Постепенное
убывание ненадежности с ростом N
соответсвует увеличению сведений об
исходном ключе или сообщении. Строго
идеально стойкой КС – это такая КС, в
которой H(K|Y)
остается равной H(K)/(
пример – простая подстановка, примененная
к искусственному языку, в которой все
буквы равновероятные и последовательные
буквы выбираются незавсимо).
Расстояние
единственности шифра- это длина
перехваченной криптограммы, при которой
ключ криптосистемы определяется с
высокой вероятностью, т.е однозначно
восстанавливается. Чем больше число,
тем лучше.
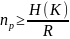 ,
H(K)
– энтропия ключа (H(K)=-
,
H(K)
– энтропия ключа (H(K)=-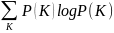 )
должна быть большой, R
– избыточность (количественная мера
взаимной зависимости символов и их
неравновероятности, R=logm-h,
h=
)
должна быть большой, R
– избыточность (количественная мера
взаимной зависимости символов и их
неравновероятности, R=logm-h,
h=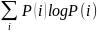 – энтропия на букву сообщения. Должна
быть маленькой)
– энтропия на букву сообщения. Должна
быть маленькой)
