
- •1)Основные понятия криптографии
- •2)Этапы становления криптографии, как науки.
- •3)Понятие криптосистемы. Классификация криптосистем. Основные требования к криптосистеме
- •4)Алгебраическая и вероятностная модели шифра.
- •5) Модели открытых текстов. Характеристики открытых текстов
- •6) Шифры замены: определение, разновидности шифров замены
- •7) Шифры перестановки: определение, разновидности шифров перестановки.
- •8) Симметричная криптосистема. Типы симметричных криптосистем.
- •9) Блочная криптосистема: понятие, принципы построения блочных криптосистем, достоинства и недостатки.
- •10) Режимы применения блочных криптосистем.
- •11) Криптосистема des.
- •Криптосистема гост 28147-89
- •14)Методы усложнения блочных симметричных криптосистем.
- •15)Поточная криптосистема: понятие, принципы построения поточных криптосистем, достоинства и недостатки.
- •16) Типы поточных криптосистем (синхронная поточная криптосистема, самосинхронизирующаяся поточная криптосистема).
- •17) Методы криптоанализа симметричных криптосистем: метод полного перебора, частотный метод, метод чтения в колонках, метод «протяжки» вероятного слова.
- •18) Линейный криптоанализ: суть метода линейного криптоанализа, этапы реализации метода.
- •19) Дифференциальный (разностный) криптоанализ: суть метода дифференциального криптоанализа, этапы реализации метода.
- •20)Понятие совершенно стойкой криптосистемы. Теорема Шеннона.
- •21) Теорема о совершенной стойкости шифра Вернама.
- •22) Идеально стойкая криптосистема. Расстояние единственности шифра.
- •23.Понятие практической стойкости криптосистемы.
- •24.Односторонняя функция. Типы используемых односторонних функций.
- •25) Криптосистема с открытым ключом: понятие криптосистемы с открытым ключом, принципы построения, достоинства и недостатки.
- •26. Криптосистема Эль-Гамаля.
- •27.Криптосистема Шамира.
- •28.Криптосистема rsa.
- •29) Криптосистема Рабина.
- •30.Понятие эллиптической кривой. Свойства точек эллиптической кривой. Выбор параметров эллиптической кривой.
- •31.Криптосистема Эль-Гамаля на эллиптической кривой.
- •32.Методы криптоанализа криптосистем с открытым ключом: метод криптоанализа «шаг младенца, шаг великана», метод исчисления порядка.
- •33) Понятие хэш-функции. Требования к хэш-функциям.
- •34.Понятие эцп. Свойства эцп.
- •35. Эцп на базе криптосистемы rsa.
- •36.Эцп на базе Эль-Гамаля.
- •37.Стандарты эцп: гост р.34.10-94. Особенности алгоритма dsa.
- •Область применения
- •38) Понятие криптографического протокола. Типы криптографических протоколов.
- •39) Протоколы управления ключами с использованием симметричных криптосистем (двусторонние и трехсторонние протоколы).
- •40) Протоколы управления ключами с использованием криптосистем с открытым ключом.
- •41) Криптографический генератор: понятие, требования к криптографическим генераторам, классификация криптографических генераторов.
- •42) Комбинированные криптографические генераторы.
- •43) Методы улучшения «элементарных» псевдослучайных последовательностей.
37.Стандарты эцп: гост р.34.10-94. Особенности алгоритма dsa.
Отечественный стандарт цифровой подписи обозначается как ГОСТ Р 34.10-94. Алгоритм цифровой подписи, определяемый этим стандартом, концептуально близок к алгоритму DSА. В нем используются следующие параметры:
р - большое простое число длиной от 509 до 512 бит либо от 1020 до 1024 бит;
q - простой сомножитель числа (р -1), имеющий длину 254...256 бит;
а - любое число, меньшее (р-1), причем такое, что аq mod p=1;
х - некоторое число, меньшее q;
Следует также отметить, что в отечественном стандарте ЭЦП параметр q имеет длину 256 бит. Западных криптографов вполне устраивает q длиной примерно 160 бит. Различие в значениях параметра q является отражением стремления разработчиков отечественного стандарта к получению более безопасной подписи.
Этот стандарт вступил в действие c начала 1995 г.
Описание.
ГОСТ Р 34.10-2001 основан на эллиптических кривых. Его стойкость основывается на сложности вычисления дискретного логарифма в группе точек эллиптической кривой, а также на стойкости хэш-функции по ГОСТ Р 34.11-94.
После подписывания сообщения М к нему дописывается цифровая подпись размером 512 бит и текстовое поле. В текстовом поле могут содержаться, например, дата и время отправки или различные данные об отправителе:
|
+ |
|
|||
|
|
Дополнение |
Данный алгоритм не описывает механизм генерации параметров, необходимых для формирования подписи, а только определяет, каким образом на основании таких параметров получить цифровую подпись. Механизм генерации параметров определяется на месте в зависимости от разрабатываемой системы.
Формирование подписи.
Алгоритм в справочном личте
Вычисление хэш-функции от сообщения М:

Вычисление
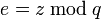 ,
и если
,
и если  ,
положить
,
положить 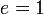 .
Где
.
Где 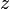 —
целое число, соответствующее
—
целое число, соответствующее 
Генерация случайного числа
 такого,
что
такого,
что 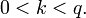
Вычисление точки эллиптической кривой
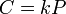 ,
и по ней нахождение
,
и по ней нахождение 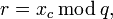 где
где  —
это координата
—
это координата 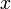 точки
точки 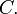 Если
Если 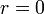 ,
возвращаемся к предыдущему шагу.
,
возвращаемся к предыдущему шагу.Нахождение
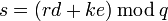 .
Если
.
Если 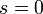 ,
возвращаемся к шагу 3.
,
возвращаемся к шагу 3.Формирование цифровой подписи
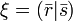 ,
где
,
где 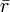 и
и 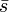 —
векторы, соответствующие
—
векторы, соответствующие  и
и  .
.
Проверка подписи.
Алгоритм в справочном листе
Вычисление по цифровой подписи
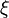 чисел
и
,
учитывая, что
,
где
и
—
числа, соответствующие векторам
и
.
Если хотя бы одно из неравенств
чисел
и
,
учитывая, что
,
где
и
—
числа, соответствующие векторам
и
.
Если хотя бы одно из неравенств  и
и  неверно,
то подпись неправильная.
неверно,
то подпись неправильная.Вычисление хэш-функции от сообщения М:
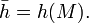
Вычисление , и если , положить . Где — целое число соответствующее
Вычисление
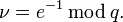
Вычисление
 и
и 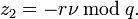
Вычисление точки эллиптической кривой
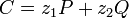 .
И определение
.
И определение 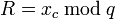 ,
где
—
координата
кривой
,
где
—
координата
кривой
В случае равенства
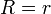 подпись
правильная, иначе — неправильная.
подпись
правильная, иначе — неправильная.
Криптостойкость.
Криптостойкость цифровой подписи опирается на две компоненты — на стойкость хэш-функции и на стойкость самого алгоритма шифрования.
Вероятность
взлома хэш-функции по ГОСТ 34.11-94
составляет ![]() при
подборе коллизии на фиксированное
сообщение и
при
подборе коллизии на фиксированное
сообщение и ![]() при
подборе любой коллизии.[1] Стойкость
алгоритма шифрования основывается на
дискретном логарифмировании в группе
точек эллиптической кривой. На данный
момент нет метода решения данной задачи
хотя бы с субэкспоненциальной сложностью.
при
подборе любой коллизии.[1] Стойкость
алгоритма шифрования основывается на
дискретном логарифмировании в группе
точек эллиптической кривой. На данный
момент нет метода решения данной задачи
хотя бы с субэкспоненциальной сложностью.
Одни
из самых быстрых алгоритмов, на данный
момент, при правильном выборе
параметров — ![]() -метод
и
-метод
и ![]() -метод
Полларда.
-метод
Полларда.
Для
оптимизированного
-метода
Полларда вычислительная сложность
оценивается как ![]() .
Таким образом для обеспечения
криптостойкости
.
Таким образом для обеспечения
криптостойкости ![]() операций
необходимо использовать 256-разрядное
операций
необходимо использовать 256-разрядное ![]() .
.
Отличия от старого госта.
Новый
и старый ГОСТы цифровой подписи очень
похожи друг на друга. Основное отличие —
в старом стандарте часть операций
проводится над полем
![]() ,
а в новом — над группой точек
эллиптической кривой, поэтому требования
налагаемые на простое число
,
а в новом — над группой точек
эллиптической кривой, поэтому требования
налагаемые на простое число ![]() в
старом стандарте(
в
старом стандарте(![]() или
или ![]() )
более жесткие, чем в новом.
)
более жесткие, чем в новом.
Алгоритм
формирования подписи
отличается только
в пункте
4. В
старом стандарте в этом пункте
вычисляются ![]() и
и ![]() и,
если
,
возвращаемся к пункту 3. Где
и,
если
,
возвращаемся к пункту 3. Где ![]() и
и ![]() .
.
Алгоритм
проверки подписи
отличается только в пункте
6.
В старом стандарте в этом пункте
вычисляется ![]() ,
где
,
где ![]() —
открытый ключ для проверки подписи,
—
открытый ключ для проверки подписи, ![]() .
Если
,
подпись правильная, иначе неправильная.
Здесь
—
простое число,
.
Если
,
подпись правильная, иначе неправильная.
Здесь
—
простое число, ![]() и
является
делителем
и
является
делителем ![]() .
.
Использование математического аппарата группы точек эллиптической кривой, позволяет существенно сократить порядок модуля , без потери криптостойкости.
Также
старый стандарт описывает механизмы
получения чисел
,
и ![]() .
.
