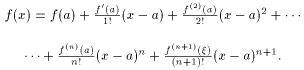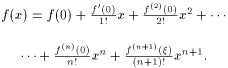Частные производные высших порядков
Мы
уже заметили, что частные производные
первого порядка ![]() мы
можем рассматривать, в предположении
их существования, как функции, заданные
в некоторой области пространства
мы
можем рассматривать, в предположении
их существования, как функции, заданные
в некоторой области пространства ![]() переменных
переменных ![]() .
От каждой из этих функций
,
в свою очередь, можно найти частные
производные:
производных
от
.
От каждой из этих функций
,
в свою очередь, можно найти частные
производные:
производных
от ![]()
производных
от ![]() :
:
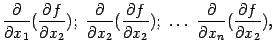
и так далее до
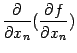 ;
всего получается
;
всего получается 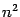 производных
производных 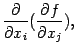 где
где 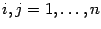 .
Производная
.
Производная 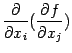 обозначается
также
обозначается
также 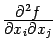 или
или 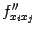 .
Эти производные называются частными
производными второго порядка от
функции
.
Эти производные называются частными
производными второго порядка от
функции 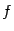 .
.Если
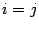 ,
то есть если второе дифференцирование
ведётся по той же переменной
,
то есть если второе дифференцирование
ведётся по той же переменной 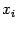 ,
что и первое, то частная производная
второго порядка
,
что и первое, то частная производная
второго порядка 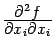 называется чистой частной
производной второго порядка по
переменной
и
более кратко обозначается
называется чистой частной
производной второго порядка по
переменной
и
более кратко обозначается 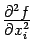 .
.Если же
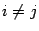 ,
то частная производная второго
порядка
называется смешанной частной
производной второго порядка.
,
то частная производная второго
порядка
называется смешанной частной
производной второго порядка.Итак, для функции можно отыскать чистых частных производных второго порядка и
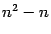 смешанных.
Ниже мы увидим, что при некоторых
дополнительных предположениях смешанные
частные производные
и
смешанных.
Ниже мы увидим, что при некоторых
дополнительных предположениях смешанные
частные производные
и 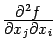 ,
отличающиеся порядком дифференцирований,
совпадают, так что различных смешанных
производных второго порядка оказывается
не
,
а вдвое меньше.
,
отличающиеся порядком дифференцирований,
совпадают, так что различных смешанных
производных второго порядка оказывается
не
,
а вдвое меньше.
Частные производные
Определение. Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина Dxz = f( x + Dx, y) – f(x, y) называется частным приращением функции по х.Можно записать
![]() . Тогда
. Тогда ![]() называется частной
производной функции
z = f(x, y) по х.
Обозначение:
называется частной
производной функции
z = f(x, y) по х.
Обозначение: ![]() Аналогично
определяется частная производная
функции по у.
Аналогично
определяется частная производная
функции по у.
![]() Геометрическим
смыслом частной
производной (допустим
Геометрическим
смыслом частной
производной (допустим ![]() )
является тангенс угла наклона касательной,
проведенной в точке N0(x0, y0, z0) к сечению
поверхности плоскостью у = у0.Полное
приращение и полный дифференциалОпределение. Для
функции f(x, y) выражение Dz = f( x + Dx, y + Dy) –
f(x, y) называется полным
приращением.Определение. Выражение
)
является тангенс угла наклона касательной,
проведенной в точке N0(x0, y0, z0) к сечению
поверхности плоскостью у = у0.Полное
приращение и полный дифференциалОпределение. Для
функции f(x, y) выражение Dz = f( x + Dx, y + Dy) –
f(x, y) называется полным
приращением.Определение. Выражение ![]() называется полным
приращением функции
f(x, y) в некоторой точке (х, у), где a1 и a2 –
бесконечно малые функции при Dх -> 0 и
Dу -> 0 соответственно.Определение: Полным
дифференциалом функции
z = f(x, y) называется главная линейная
относительно Dх и Dу приращения функции
Dz в точке (х, у).
называется полным
приращением функции
f(x, y) в некоторой точке (х, у), где a1 и a2 –
бесконечно малые функции при Dх -> 0 и
Dу -> 0 соответственно.Определение: Полным
дифференциалом функции
z = f(x, y) называется главная линейная
относительно Dх и Dу приращения функции
Dz в точке (х, у).
![]()
Для функции произвольного числа переменных:
![]()
Частные
производные высших порядковЕсли
функция f(x, y) определена в некоторой
области D, то ее частные производные ![]() и
и ![]() тоже
будут определены в той же области или
ее части.
Будем
называть эти производные частными
производными первого порядка.
Производные
этих функций будут частными
производными второго порядка.
тоже
будут определены в той же области или
ее части.
Будем
называть эти производные частными
производными первого порядка.
Производные
этих функций будут частными
производными второго порядка.
![]()
![]() Продолжая
дифференцировать полученные равенства,
получим частные производные более
высоких порядков.
Продолжая
дифференцировать полученные равенства,
получим частные производные более
высоких порядков.
Определение. Частные
производные вида ![]()
![]() и
т.д. называются смешанными
производными.
и
т.д. называются смешанными
производными.
Производные и дифференциалы высших порядков
Предположим, что функция f'(x) является дифференцируемой в некоторой точке x интервала (a,b), то есть имеет в этой точке производную. Тогда данную производную называют второй произвоьдной и обозначают f(2)(x), f''(x) или y(2), y''(x). Аналогично можно ввести понятие второй , третьей и т. д. производных. По индукции можно ввести понятие n- ой производной:
y(n) = (y(n-1))'. |
(6) |
Функцию, имеющую на некотором множестве конечную производную порядка n,называют n раз дифференцируемой на этом множестве. Методика нахождения производных высших порядков предполагает умение находить производные первого порядка, о чем говорит формула (6).
Если u(x), v(x) две дифференцируемые функции, то для нахождения производной их произведения справедлива формула Лейбница
(u(x)v(x))(n) = u(n)v+nu(n-1)v'+(n(n-1)/2)u(n-2)v''+...+ uv(n) =
= k = 0nCnku(n-k)v(k),
где
Cnk = (n(n-1)(n-2)...(n-k+1))/k!, u(0) = u, v(0) = v.
Данная формула Лейбница особенно эффективна в случае, когда одна из перемножаемых функций имеет конечное число отличных от нуля производных и легко вычислить производные другой функции.
Пример 9. Пусть y = ex(x2-1). Найти y(10). Положим u(x) = ex, v(x) = (x2-1). Согласно формуле Лейбница
y(10) = (ex)(25)(x2-1)+10(ex)(9)(x2-1)'+(10· 9/2) (ex)(8)(x2-1)'',
так как следующие слагаемые равны нулю. Поэтому
y(10) = ex(x2-1)+10ex2x+(10· 9/2)ex (2) = ex(x2+20x+89)
Рассмотрим выражение для первого дифференциала
dy = f'(x)dx.
Пусть функция, стоящая в правой части, является дифференцируемой функцией в данной точке x. Для этого достаточно, чтобы y = f(x), была дифференцируема два раза в данной точке x, а аргумент либо является независимой переменной, либо представляет собой дважды дифференцируемую функцию.
Теорема
8 (теорема Тейлора). Пусть
функция f(x) имеет
в точке x = a и некоторой ее окрестности
производные порядка n+1.
Тогда между точками a и x a
найдется такая точка ![]() ,
что справедлива следующая формула:
,
что справедлива следующая формула:
|
(10) |
Формула (10) называется формулой Тейлора, а выражение
![]()
представляет остаточный член в форме Лагранжа. Заметим, что если функцияf(n+1)(x) ограничена в окрестности точки a, тогда остаточный член является бесконечно малой при x a более высокого порядка, чем (x-a)n. Таким образом, остаточный член можно записать в виде
Rn+1(x) = o((x-a)n) при x a.
Данная форма записи остаточного члена называется формой Пеано.
Формулой Маклорена называется формула Тейлора при a = 0:
|
(11) |
Остаточный член в форме Пеано для формулы Маклорена имеет вид
Rn+1 = o(xn) при x 0.
Приведем разложения некоторых элементарных функций по формуле Маклорена
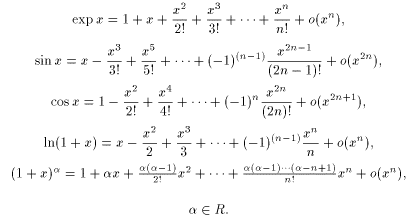
.
Экстремум функции нескольких переменных.
Необходимые и достаточные условия
существования экстремума
Определение
7. Точка ![]() называется
точкой минимума (максимума) функции
называется
точкой минимума (максимума) функции ![]() ,
если существует такая окрестность
точки
,
если существует такая окрестность
точки ![]() ,
что для всех точек
,
что для всех точек ![]() из
этой окрестности выполняется
неравенство
из
этой окрестности выполняется
неравенство ![]() ,
(
,
(![]() ).
Точки
минимума и максимума функции
называются
точками экстремума, а значения функции
в этих точках – экстремумами функции
(минимумом и максимумом
соответственно).
Заметим,
что минимум и максимум функции имеют
локальный характер, так как значение
функции в точке
сравнивается
с ее значениями в точках, достаточно
близких к
.
Теорема
1 (необходимые условия экстремума).
Если
).
Точки
минимума и максимума функции
называются
точками экстремума, а значения функции
в этих точках – экстремумами функции
(минимумом и максимумом
соответственно).
Заметим,
что минимум и максимум функции имеют
локальный характер, так как значение
функции в точке
сравнивается
с ее значениями в точках, достаточно
близких к
.
Теорема
1 (необходимые условия экстремума).
Если ![]()
–
точка экстремума
дифференцируемой функции
,
то ее частные производные ![]() и
и ![]() в
этой точке равны нулю:
в
этой точке равны нулю: ![]()
![]() .
Точки,
в которых частные производные первого
порядка равны нулю, называются
критическими или стационарными. В
критических точках функция
может
иметь экстремум, а может и не иметь.
Теорема
2 (достаточное условие экстремума).
Пусть функция
:
а) определена в некоторой окрестности
критической точки
,
в которой
.
Точки,
в которых частные производные первого
порядка равны нулю, называются
критическими или стационарными. В
критических точках функция
может
иметь экстремум, а может и не иметь.
Теорема
2 (достаточное условие экстремума).
Пусть функция
:
а) определена в некоторой окрестности
критической точки
,
в которой ![]() и
;
б) имеет непрерывные частные производные
второго порядка
и
;
б) имеет непрерывные частные производные
второго порядка ![]()
![]()
![]() .
Тогда, если
.
Тогда, если ![]() ,
то функция
,
то функция ![]() в
точке
имеет
экстремум: максимум, если А<0; минимум,
если А>0; если
в
точке
имеет
экстремум: максимум, если А<0; минимум,
если А>0; если ![]() ,
то функция
в
точке
экстремума
не имеет. В случае
,
то функция
в
точке
экстремума
не имеет. В случае ![]() вопрос
о наличии экстремума остается открытым.
вопрос
о наличии экстремума остается открытым.