
3.Производ сложных и неяв ф-ий
1)Функция
одной переменной ![]() – это
правило, по которому каждому значению
независимой переменной
– это
правило, по которому каждому значению
независимой переменной ![]() соответствует
одно и только одно значение функции
соответствует
одно и только одно значение функции ![]() .
.
Переменная называется независимой переменной или аргументом. Переменная называется зависимой переменной или функцией.
Грубо говоря, буковка «игрек» в данном случае – и есть функция.
До сих пор мы рассматривали функции, заданные в явном виде. Что это значит? Устроим разбор полётов на конкретных примерах.
Рассмотрим
функцию ![]()
Мы видим, что слева у нас одинокий «игрек» (функция), а справа – только «иксы». То есть, функция в явном виде выражена через независимую переменную .
Рассмотрим
другую функцию: ![]()
Здесь
переменные
и
расположены
«вперемешку». Причем никакими
способами невозможно выразить
«игрек» только через «икс». Что это за
способы? Перенос слагаемых из части в
часть со сменой знака, вынесение за
скобки, перекидывание множителей по
правилу пропорции и др. Перепишите
равенство
и
попробуйте выразить «игрек» в явном
виде: ![]() .
Можно крутить-вертеть уравнение часами,
но у вас этого не получится.
.
Можно крутить-вертеть уравнение часами,
но у вас этого не получится.
Разрешите познакомить: – пример неявной функции.
2)
Как
дифференцировать ![]() Здесь
у нас сложная
функция.
Почему? Вроде бы под синусом всего одна
буква «игрек». Но, дело в том, что всего
одна буква «игрек» – САМА
ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ(см.
определение в начале урока). Таким
образом, синус – внешняя функция,
–
внутренняя функция. Используем правило
дифференцирования сложной функции
Здесь
у нас сложная
функция.
Почему? Вроде бы под синусом всего одна
буква «игрек». Но, дело в том, что всего
одна буква «игрек» – САМА
ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ(см.
определение в начале урока). Таким
образом, синус – внешняя функция,
–
внутренняя функция. Используем правило
дифференцирования сложной функции ![]() :
:
![]()
4.Производ по направ. Град и его св-ва
Значение предела
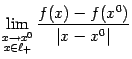
называется производной функции ![]() по
направлению оси (или луча)
по
направлению оси (или луча) ![]() (илипо
направлению вектора
(илипо
направлению вектора ![]() ),
вычисленной в точке
),
вычисленной в точке ![]() .
Производная по направлению
обозначается
.
Производная по направлению
обозначается 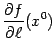 или
или 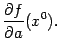
Смысл
определения производной по направлению --
в том, что она задаётмгновенную
скорость изменения значений
функции
при
прямолинейном и равномерном движении
точки ![]() вдоль
оси
в
момент
вдоль
оси
в
момент ![]() .
.
2)
Градие́нт (от лат. gradiens,
род. падеж gradientis —
шагающий, растущий) — вектор,
своим направлением указывающий
направление наискорейшего возрастания
некоторой величины ![]() ,
значение которой меняется от одной
точки пространства к другой (скалярного
поля),
а по величине (модулю) равный быстроте
роста этой величины в этом направлении.
,
значение которой меняется от одной
точки пространства к другой (скалярного
поля),
а по величине (модулю) равный быстроте
роста этой величины в этом направлении.
Используя правило
дифференцирования сложной функции,
нетрудно показать, что производная
функции
по
направлению ![]() равняется
скалярному произведению
градиента
на единичный вектор
равняется
скалярному произведению
градиента
на единичный вектор ![]() :
:
![]()
Таким образом, для вычисления производной по любому направлению достаточно знать градиент функции, то есть вектор, компоненты которого являются её частными производными.
5. Касат плоск и нормаль поверхти
Определение 1. Касательной
плоскостью к поверхности ![]() в
данной точке P (x0,
y0,
z0) называется
плоскость, проходящая через точку Р и
содержащая в себе все касательные,
построенные в точке Р ко всевозможным
кривым на этой поверхности, проходящим
через точку Р.
в
данной точке P (x0,
y0,
z0) называется
плоскость, проходящая через точку Р и
содержащая в себе все касательные,
построенные в точке Р ко всевозможным
кривым на этой поверхности, проходящим
через точку Р.
Определение 2. Нормалью
к поверхности s в точке Р называется
прямая, проходящая через точку Р и
перпендикулярная к касательной
плоскости, построенной в этой точке.
![]() –
уравнение нормали, построенной в
точке Р к
поверхности s .
–
уравнение нормали, построенной в
точке Р к
поверхности s .
6.Необход услов и достаточ услов экстремума:1)Теорема (Необходимое условие экстремума) Если функция нескольких переменных u = f(x1, x2, … , xn) имеет экстремум в некоторой точке, то в этой точке каждая ее частная производная равна нулю или не существует. Внутренние точки из области определения функции, в которых выполняются необходимые условия экстремума, называются критическими. Если в критической точке функция дифференцируема, то такая точка называется стационарной.
2)Таким образом, достаточным условием экстремума функции нескольких переменных в ее стационарной точке является знакоопределенность (положительная или отрицательная определенность) дифференциала 2–го порядка в этой точке.
7.Условный экстремум:Пусть функция
|
|
(1) |
определена в некоторой области D Rn и ее аргументы не являются независимыми переменными, а связаны k (k<n) соотношениями:
|
|
(2) |
Условия (2) называются уравнениями связи.
Пусть координаты точки M0(x10, … ,xn0) D удовлетворяют уравнениям связи (2).
Точка M0(x10, … ,xn0) называется точкой условного максимума (минимума) функции (1) при условиях связи (2), если существует такая окрестность Oδ(M0) точки M0 , что для любой точки M(x1, … ,xn) Oδ(M0) , координаты которой удовлетворяют уравнениям связи (2), выполняется неравенство f(M) ≤ f(M0) (f(M) ≥ f(M0)) .
8. Определение первообразной и неопределенного интеграла
Функция F(x) называется первообразной функции f(x), если
![]()
Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функцииf(x) и обозначается как
![]()
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины.
![]()
![]()
![]()
![]()
9.Таблица интегралов Основные приемы интегрирования
Простейшие задачи, в которых нужно проинтегрировать элементарные функции, решаются при помощи таблицы первообразных. В более сложных случаях нужно знать ряд приемов, сводящих в конечном итоге вычисляемый интеграл к интегралам от табличных функций. Одним из таких приемов является метод замены переменного .
Пусть
определены дифференцируемые
функции f ( x ) и g ( t ),
а также сложная функция g ( f ( x )).
Пусть ![]() Тогда
Тогда ![]() Это
означает, что
Это
означает, что
![]()
Иногда,
вычисляя интеграл ![]() полезно
перейти к новой переменной.
Пусть x = g ( t )
монотонная дифференцируемая функция,
полезно
перейти к новой переменной.
Пусть x = g ( t )
монотонная дифференцируемая функция, ![]() –
обратная ей функция.
Тогда
–
обратная ей функция.
Тогда ![]() Обозначая
Обозначая ![]() получим f ( x ) dx = u ( t ) dt .
Если
получим f ( x ) dx = u ( t ) dt .
Если ![]() то
то
![]()
Этот метод называется методом подстановки .
Пусть
функции u ( x ) и v ( x )
имеют непрерывные на D производные.
Тогда
![]() Функция uv имеет
непрерывную производную на D ,
и
Функция uv имеет
непрерывную производную на D ,
и ![]() Интегрируя
обе части этого равенства, получим
Интегрируя
обе части этого равенства, получим ![]() Относя
константу интегрирования к
интегралу
Относя
константу интегрирования к
интегралу ![]() получаем
доказываемую формулу.
получаем
доказываемую формулу.
Эта
формула описывает метод интегрирования
по частям . Она сводит вычисление
интеграла ![]() к
вычислению интеграла
к
вычислению интеграла ![]()
10. Определенные интегралы (интеграл Римана). Пусть действительная функция f(x) определена и ограничена на ограниченном замкнутом интервале [a, b]. Разобъем этот интервал на n частичных интервалов точками
a = x0 < x1 < x2 < ... < xn = b.
Выберем
в каждом из частичных интервалов по
произвольной точке ![]()
![]()
![]() и
составим сумму (интегральная сумма)
и
составим сумму (интегральная сумма) ![]()
![]()
![]() .
.
Если
существует предел интегральной суммы
при стремлении к нулю длины наибольшего
частичного интервала разбиения: ![]()
![]() ,
то функция f(x)
называетсяинтегрируемой
в смысле Римана на
интервале [a, b].
,
то функция f(x)
называетсяинтегрируемой
в смысле Римана на
интервале [a, b].
11..Определенный интеграл. Необходимое условие существования.
Пусть
ф-ция f(x)
определена на отрезке [a,b].
Разобъем отрезок [a,b]
на n
производных частей a=x<x1<x2<…<xn=b.
На каждом из отрезков [x(i-1),
xi]произвольным
образом выберем т. «кси» i [xi-1,xi].
Обозначим через
[xi-1,xi].
Обозначим через
 xi=xi-x(i-1)
и «кси»=(кси1, кси 2, … кси n).
Разбиение (a=x0<x1<…<xn=b)
обозначим через «тау». Составим сумму.
S
f(тау,
кси)=f(кси1
xi=xi-x(i-1)
и «кси»=(кси1, кси 2, … кси n).
Разбиение (a=x0<x1<…<xn=b)
обозначим через «тау». Составим сумму.
S
f(тау,
кси)=f(кси1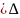 xi+f(кси2)
xi+…+f(кси
n)
xi=
xi+f(кси2)
xi+…+f(кси
n)
xi= составим такую сумму, кот.на.интегральной
суммой ф-ции f(x)
на [a,b]
с параметром кси и тау.Опр1.Пусть d(тау)
-
составим такую сумму, кот.на.интегральной
суммой ф-ции f(x)
на [a,b]
с параметром кси и тау.Опр1.Пусть d(тау)
-
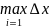 ,
- диаметр разбиения. Если
,
- диаметр разбиения. Если
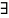 конечн.предел
конечн.предел
 ,
не зависящей от способа разбиения
отрезка a,b
и выбора точек из набора кси, то этот
предел наз. Определенным интегралом
ф-ции f(x)
и обоз-ся
,
не зависящей от способа разбиения
отрезка a,b
и выбора точек из набора кси, то этот
предел наз. Определенным интегралом
ф-ции f(x)
и обоз-ся
 .
Необходимое
условие:
если f(x)
интегрируема на отрезке [a,b],то
она ограничена на этом отрезке. НО
обратное – неверно. Те
такие
ф-ции, кот.явл.ограниченными на нек.
Отрезке, но не явл.интегрироваными на
дан.отрезке.
.
Необходимое
условие:
если f(x)
интегрируема на отрезке [a,b],то
она ограничена на этом отрезке. НО
обратное – неверно. Те
такие
ф-ции, кот.явл.ограниченными на нек.
Отрезке, но не явл.интегрироваными на
дан.отрезке.
12. Замена переменной в определенном интеграле.
Пусть
f(x)
С[ab]
и пусть
 (t)
С
и D
[ab],
причем: 1)
(t)
С
и D
[ab],
причем: 1)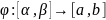 2)
2)
 3)
3) =a,
=a,
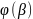 =b.Тогда
=b.Тогда
 док-во: по формуле Н-Л
док-во: по формуле Н-Л
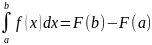 ,
где F(x)
– одна из первообразных ф-ции
f(x).Рассмотрим
ф-цию F(
,
где F(x)
– одна из первообразных ф-ции
f(x).Рассмотрим
ф-цию F(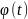 ).
(F(
).
(F( )’=F’(
)*
)’=F’(
)*
 =f(
)*
=f(
)*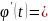 F(
)-
первообр.ф-ции f(
)*
=>
по формуле Н-Л:
F(
)-
первообр.ф-ции f(
)*
=>
по формуле Н-Л:

13-14.
Основные свойства определенного
интеграла. Оценки интегралов.
1.

 2.Каковы бы ни были точки a,b
и c:
2.Каковы бы ни были точки a,b
и c:
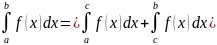 3.k-нект.число.
Тогда
3.k-нект.число.
Тогда
 4.
4.
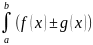 dx=
dx= 4’Св-во линейности:
4’Св-во линейности:
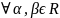
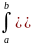 f(x)+
f(x)+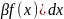 =
=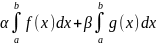
15.
5Теорема о
среднем. Пусть f(x)
С[ab].Тогда
найдется такая с из [ab],
что
 f(c)*(b-a).
f(c)*(b-a).
16. . Формула Ньютона-Лейбница.
Теорема. Пусть f(x) С [ab] ипусть F(x) – одна из первообразных ф-ции f(x).Тогда .
17.
Геометрические
приложения определенного интеграла.
площадь криволинейной трапеции:пусть
f(x)-
опеределена на [ab],
не отриц-на.f(x)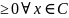 [ab].Тогда
S=
[ab].Тогда
S=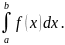 длина дуги кривой:пусть
f(x)
длина дуги кривой:пусть
f(x)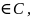 D
[ab].
L=
D
[ab].
L=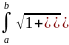 .
объем тела вращения:
f(x)
[ab].
V=
.
объем тела вращения:
f(x)
[ab].
V= .
площадь
поверхности вращения: f(x)
.
площадь
поверхности вращения: f(x) [ab]
и f
‘(x)
С[ab].
S=2
[ab]
и f
‘(x)
С[ab].
S=2 .
.
18. длина дуги кривой:пусть f(x) D [ab]. L= . объем тела вращения: f(x) [ab]. V= . площадь поверхности вращения: f(x) [ab] и f ‘(x) С[ab]. S=2 .
19.
.Несобственные
интегралы 1-го и 2-го рода. Опр.
Пусть f(x)опр-на
на пром-ке[a,+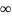 ]
и интегрир-ма в люб.его части [a,R](т.е.
]
и интегрир-ма в люб.его части [a,R](т.е.
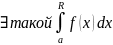 ).
Тогда если
).
Тогда если
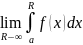 ,
то он наз.неопред. интег-ом 1го рода и
обознач
,
то он наз.неопред. интег-ом 1го рода и
обознач
 .
Опр. Пусть f(x)
опр-на на проме-ке [ab)
и f(x)
не ограничена в люб.точке окр-ти точка
b,
но
.
Опр. Пусть f(x)
опр-на на проме-ке [ab)
и f(x)
не ограничена в люб.точке окр-ти точка
b,
но
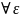 >0
ф-ция f(x)
интегр-ма на отрезке[a,b-
>0
ф-ция f(x)
интегр-ма на отрезке[a,b- ]
, тогда если
]
, тогда если
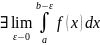 то он наз-ся несобственным интергралом
2го рода
то он наз-ся несобственным интергралом
2го рода
20-21.
Дифференциальные уравнения: основные
понятия и определения.Опр.:
Ур-ие вида f(x,y,y’)=0
(1)
наз-ся диф-ым ур-ем 1-го порядка, где x
– перем-я, y–иско-мая
ф-я, y’
– ее производная.Опр.:
Поряд-ком
диф-го ур-ия наз-ся порядок старшей
производной, входящей в него. Если ур-ие
(1) можно решить относительно y’,
то оно примет вид: y’=f
(x,y)
(2),
к-ое наз-ют диф-ым
ур-ем, разрешенным относитель-но
произ-ой.
Опр. Решение ур-я (2) наз всякая ф-ция
y= ,кот.при
подстановке в ур-е(2) обращает его в
тождество, те
’(x)
,кот.при
подстановке в ур-е(2) обращает его в
тождество, те
’(x)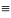 f(x,
)
Опр. График решения диф-ого ур-я (2) наз
интегральн.кривой. Опр. Диф.ур-е y’=f(xy)с
задан. начальн. условиями.
f(x,
)
Опр. График решения диф-ого ур-я (2) наз
интегральн.кривой. Опр. Диф.ур-е y’=f(xy)с
задан. начальн. условиями.
 наз. Задачей Коши.
наз. Задачей Коши.
Теорема.
Пусть ф-ция f(xy)
непрер в нек. обл. G
и
такая
константа L,
что для люб пары точек (x,y1),
(x,y2)
G
следует, что |f(x,y1)-f(x,y2)|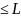 *|y1-y2|
- ур-е Лепшиц.
*|y1-y2|
- ур-е Лепшиц.
Общее
и частное решение диф-го ур-ия. Опр.:
Общим
решением ур-ия (2) в области G
наз-ся ф-ия y=(x,C),
зависящая от неизвестной x
и произвольной постоянной С, такая, что
 С=С0 –фция (x,C)
явл-ся решением ур-я (2) и
(x0y0)
С=С0 –фция (x,C)
явл-ся решением ур-я (2) и
(x0y0)
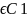
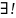 С=С1, такая что U(x,C0)
яв-ся решением задачи Коши.Опр.:
Частным
решением ур-я
(2) наз-ся ф-ия y=(x,C0),
полученная из общего решения ур-я(1)
заменой постоянной с определенным
значением. С гео-метр-ой точки зрения
частному решению соответствует одна
интегральная кривая, а общему – семейство
интегральных кри-вых.
С=С1, такая что U(x,C0)
яв-ся решением задачи Коши.Опр.:
Частным
решением ур-я
(2) наз-ся ф-ия y=(x,C0),
полученная из общего решения ур-я(1)
заменой постоянной с определенным
значением. С гео-метр-ой точки зрения
частному решению соответствует одна
интегральная кривая, а общему – семейство
интегральных кри-вых.
22. Однородные ур-ия. Опр.: Ур-ие y’= f(x, y) наз-ся однородным, если ф-я f(x,y) м. б. представлена как ф-я отношения своих аргументов. Схема решения: 1). обозначить y/x=U, y=Ux; 2). y’=U’x+U; 3) подставить y и y’ в данное ур-ие, решить его относительно ф-ии U; 4) сделать обратную замену, т.е. U выразить через x и y.
23. Дифференциальные уравнения второго порядка, допускающие понижения порядка.
Опр:
ур-е вида F(x,y,y’,y’’)=0,
где х- независимая переменная, у- искомая
фун-я, y’,y’’- ее производные, назыв диф
ур-ем 2-го порядка. Обычно расматр-ся
ур-я, кот. могут быть разрешены от-но
y’’, т.е. ур-е вида: y’’=f(x,y,y’) (1) Опр:
решением ур-я (1) назыв-ся фун-я y=
(x),кот.
обращает его в тождество
’’(x)
f(x, .
Теорема (Коши):
.
Теорема (Коши):
 Общ.решение
ДУ(1): ф-я у=φ(х1,С1,С2) зависящая от х и 2-х
произвольных постоянных С1,С2, назыв
общим решением ур-я (1). Если она яв-ся
решением ур-я (1) при люб-х значениях
С1,С2 и если при начал-х условиях сущ-т
единственные значения постоянных
С1=С1º ,С2=С2º, такие что ф-я у=φ(х,С1º,С2º)
удовлетворяет нач-м условиям. Опр: любая
ф-я у=φ(х,С1º,С2º) полученная из общего
решения ур-я (1) при опред-х значениях
постоянных С1 и С2 назыв частным
решением
ур-я (1). Рассм.
3 случая когда решение ур-я (1) с помощью
замены переменной сводится к решению
ур-я 1-ого порядка. Такое преобразование
ур-я назыв. понижением
порядка.
1.Ур-е
вида у’’=f
(х) (нет у,
у’), введем новую ф-цию z (x)=y, y’’=z (x),
подставим в ур-е y’’ получим ур-е 1-ого
порядка решив к-ое найдем ф-цию z (x) а
значит нашли у' и теперь решая ур-е для
у’ найдем искомую ф-цию у. y’=x. 2.Ур-е
вида y’’=f
(x,
y’)
(нет у) введем вспомогательную ф-цию z
(x)=y’,
тогда y’’=z
(x)
подставив все в данное ур-е получим
ур-е 1-ого порядка, решив к-ое найдем
ф-цию z
(x),
т.е. y’
и решая ещё раз ур-е найдем искомую
ф-цию y’.
3.Ур-е
вида y’’=f
(y,
y’)
введем вспомогательную ф-цию z
(y)
так что y’=z.
y’’
= z
dz/dy.
Подставим в данное ур-е y’’
и y’
и решив его найдем z,
т.е. y’
и решив ур-е для y’
найдем y.
Общ.решение
ДУ(1): ф-я у=φ(х1,С1,С2) зависящая от х и 2-х
произвольных постоянных С1,С2, назыв
общим решением ур-я (1). Если она яв-ся
решением ур-я (1) при люб-х значениях
С1,С2 и если при начал-х условиях сущ-т
единственные значения постоянных
С1=С1º ,С2=С2º, такие что ф-я у=φ(х,С1º,С2º)
удовлетворяет нач-м условиям. Опр: любая
ф-я у=φ(х,С1º,С2º) полученная из общего
решения ур-я (1) при опред-х значениях
постоянных С1 и С2 назыв частным
решением
ур-я (1). Рассм.
3 случая когда решение ур-я (1) с помощью
замены переменной сводится к решению
ур-я 1-ого порядка. Такое преобразование
ур-я назыв. понижением
порядка.
1.Ур-е
вида у’’=f
(х) (нет у,
у’), введем новую ф-цию z (x)=y, y’’=z (x),
подставим в ур-е y’’ получим ур-е 1-ого
порядка решив к-ое найдем ф-цию z (x) а
значит нашли у' и теперь решая ур-е для
у’ найдем искомую ф-цию у. y’=x. 2.Ур-е
вида y’’=f
(x,
y’)
(нет у) введем вспомогательную ф-цию z
(x)=y’,
тогда y’’=z
(x)
подставив все в данное ур-е получим
ур-е 1-ого порядка, решив к-ое найдем
ф-цию z
(x),
т.е. y’
и решая ещё раз ур-е найдем искомую
ф-цию y’.
3.Ур-е
вида y’’=f
(y,
y’)
введем вспомогательную ф-цию z
(y)
так что y’=z.
y’’
= z
dz/dy.
Подставим в данное ур-е y’’
и y’
и решив его найдем z,
т.е. y’
и решив ур-е для y’
найдем y.
