8º. Многочлены с действительными коэффициентами.
Пусть
но
.
Такой многочлен называется многочленом
с действительными коэффициентами.
Лемма
5.
Если
− корень многочлена
с действительными коэффициентами, то
− также корень
.
Доказательство.
Так как
− корень многочлена
взяв комплексное сопряжение
■
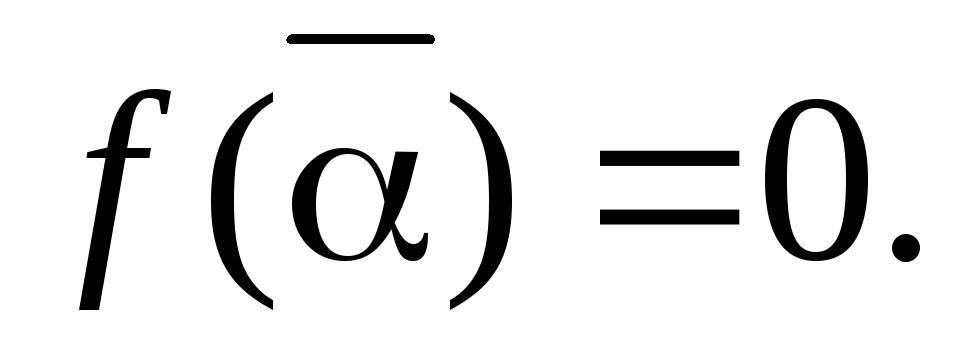Из леммы 5
если
то из
Если
то
− многочлен с действительными
коэффициентами, т.к.
Лемма
6.
Если
− корень кратности
многочлена
с действительными коэффициентами, то
− тоже
−кратный
корень
.
Доказательство.
Пусть
−
−кратный
корень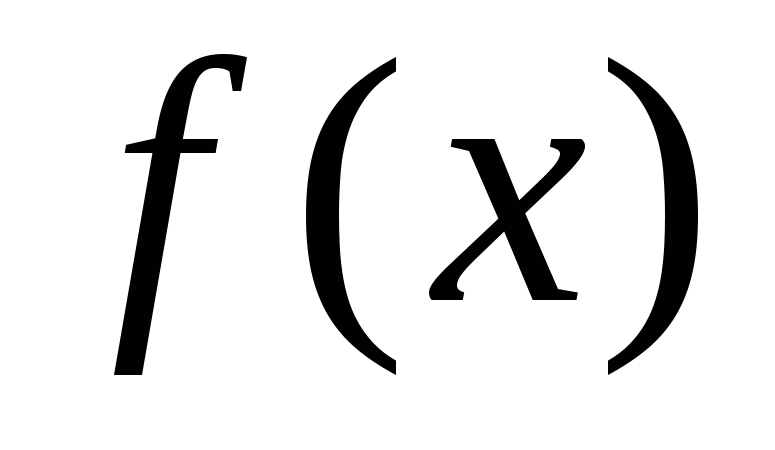
и пусть
.
Тогда
,
где
Отсюда имеем
где
Многочлен
-
многочлен с действительными коэффициентами
как частное двух многочленов с
действительными коэффициентами и
определяется однозначно. Т.о,
что противоречит лемме 5
не может быть больше
.
Аналогично,
не
может быть меньше
■
Лемма
7.
многочлен
с действительными коэффициентами
нечетной степени имеет хотя бы один
действительный корень.
Определение
9.
Многочлен
,
называется неприводимым
(над полем
),
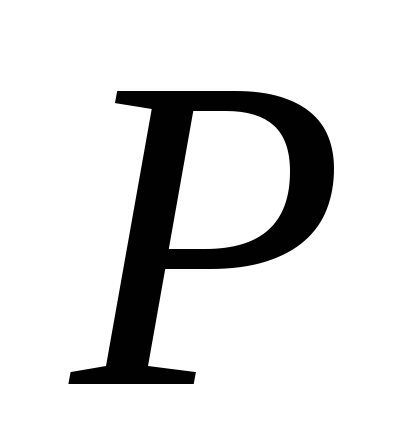если его нельзя представить в виде
произведения многочленов из
,
степени которых меньше
.
Очевидно, что
т.е.
а также вида
являются неприводимыми.
Теорема
9.
Для всякого
имеет место разложение на неприводимые
множители вида
(6)
где
,
Это разложение единственно с точностью
до перестановки сомножителей.
Доказательство.
Пусть
Рассмотрим многочлен
над С с теми же коэффициентами. Согласно
леммам 5 и 6 его корни можно расположить
в последовательности:
где
Согласно следствию 1 к ОТА, имеем:
.
Полагая
имеем
для
получим (6).
Для доказательства
единственности заметим, что правая
часть (6) равна
для
.
Но набор неприводимых множителей
определяется корнями
разложение единственно. ■
Следствие. Всякий
неприводимый многочлен над
имеет вид :
,
,
,
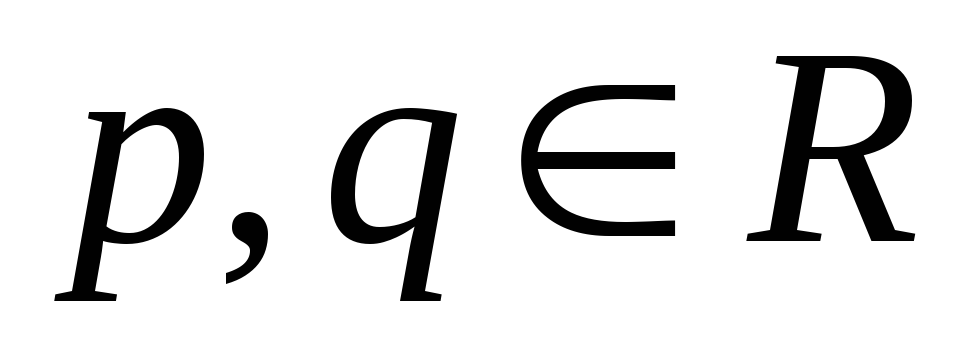или
.