
§ 3. Многочлены
1о. Эвристические соображения.
Пусть
![]() – поле. Тогда многочленом (полиномом)
от одной
переменной
– поле. Тогда многочленом (полиномом)
от одной
переменной
![]() с
коэффициентами из
с
коэффициентами из
![]() называется выражение вида
называется выражение вида
![]()
Здесь под
![]() понимается
некоторый символ, который может принимать
любые значения из
понимается
некоторый символ, который может принимать
любые значения из
![]() .
.
Многочлен можно понимать как:
-
формальное выражение;
-
как функцию
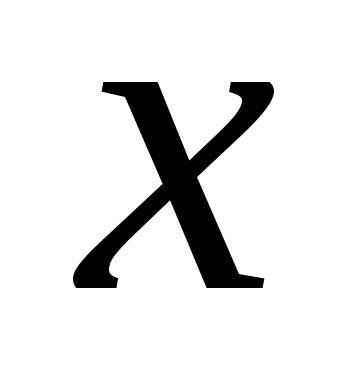 ,
если
,
если
 .
.
Ключевой вопрос: что значит, что два многочлена равны?
Если следовать
первому пункту, то
![]()
равносильно
выполнению равенств
![]() Если
второму,
то
Если
второму,
то
![]() должно
выполняться равенство
должно
выполняться равенство
![]() .
.
Легко видеть, что если многочлены равны как формальные выражения, то они равны как функции. Обратно неверно.
Пример.
Если![]()
![]() с операциями, введенными в примере 5 из
примеров колец (см. п.
3° из
§ 2), то многочлены
с операциями, введенными в примере 5 из
примеров колец (см. п.
3° из
§ 2), то многочлены
![]() и
и
![]() совпадают как функции, но различны как
формальные выражения. Тоже самое
совпадают как функции, но различны как
формальные выражения. Тоже самое
![]() и
и
![]() .
.
В
дальнейшем будем
рассматривать многочлены как формальные
выражения. Более того, для удобства
формальной записи алгебраических
операций многочлены желательно
рассматривать как сумму бесконечного
числа слагаемых вида
![]() с конечным числом отличных от нуля
слагаемых:
с конечным числом отличных от нуля
слагаемых:
![]() Тогда формулы для суммы и произведения
многочленов примут вид:
Тогда формулы для суммы и произведения
многочленов примут вид:
![]() ;
;
![]() ,
,
где
![]() .
.
2O. Точные определения.
Пусть
![]() – поле.
– поле.
Определение
1.
Многочленом одной переменной с
коэффициентами из
![]() называется бесконечная последовательность
называется бесконечная последовательность
![]() ,
в которой все элементы, кроме конечного
числа, равны нулю.
,
в которой все элементы, кроме конечного
числа, равны нулю.
Множество многочленов
с коэффициентами из поля![]() обознается
обознается![]()
![]()
![]() .
.
Введем операции сложения и умножения многочленов.
Пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
где
,
где
![]() .
.
Очевидно, что
![]() и
и
![]() имеют лишь конечное число ненулевых
членов, т.е. являются многочленами. При
этом, если
имеют лишь конечное число ненулевых
членов, т.е. являются многочленами. При
этом, если
![]() имеет
имеет
![]() членов, а
членов, а
![]() ненулевых членов, то
ненулевых членов, то
![]() –
не более чем
–
не более чем
![]() ,
а
,
а
![]() – не более чем
– не более чем
![]() ненулевых членов.
ненулевых членов.
Теорема
1.
 – коммутативное кольцо с единицей и
без делителей нуля.
– коммутативное кольцо с единицей и
без делителей нуля.
Доказательство.
![]() – абелева группа – очевидно. При этом
нулевой элемент
– абелева группа – очевидно. При этом
нулевой элемент![]() .
.
Проверим ассоциативность умножения. Пусть
![]() .
.
Необходимо доказать,
что
![]() .
Имеем:
.
Имеем:
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() ,
,
и
![]() ,
где
,
где
![]() ,
,
т.е. ассоциативность умножения выполняется.
Проверим дистрибутивность, т.е. выполнение равенств
![]() .
.
Имеем![]() где
где
![]() ;
;
![]() где
где
![]() .
.
Аналогично доказывается второе равенство.
Проверим коммутативность умножения. Имеем
![]() ,
где
,
где
![]() и
и
![]() ,
где
,
где
![]()
![]() силу коммутативности
умножения в
силу коммутативности
умножения в
![]() .
.
Легко проверить,
что
![]() – единица в
– единица в
![]() ,
так как
,
так как
![]() .
.
Покажем, что в
![]() нет делителей нуля. Пусть
нет делителей нуля. Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() ,
т.к.
,
т.к.
![]() не имеет делителей нуля. Следовательно,
не имеет делителей нуля. Следовательно,
![]() – кольцо без делителей нуля.
■
– кольцо без делителей нуля.
■
Рассмотрим
![]() .
.
Очевидно, что
![]()
![]() .
.
Следовательно,
множество
![]() можно отождествить с
можно отождествить с
![]() (т.е. построить изоморфизм между этими
кольца, причем
(т.е. построить изоморфизм между этими
кольца, причем
![]() ставится в соответствие
ставится в соответствие
![]() .)
.)
Обозначим
![]() (т.к.
(т.к.
![]() ).
).
Лемма
1.
Пусть
![]() .
Тогда
.
Тогда
![]() .
.
Доказательство.
Так как
![]() ,
то легко видеть, что
,
то легко видеть, что
![]() . Тогда
. Тогда
![]() ,
и, значит
,
и, значит
![]()
Терминология. Пусть
![]() .
Тогда
.
Тогда
![]() – свободный член. Если
– свободный член. Если
![]() ,
то
,
то
![]() –
степень многочлена. Пишут
–
степень многочлена. Пишут
![]() (degree),
(degree),
![]() – старший коэффициент
– старший коэффициент
![]() ,
,
![]() ,
,
![]() – переменная.
– переменная.
Следствие.
![]() .
Выполняется
.
Выполняется
![]() .
.
При этом
![]() ,
,
![]() .
.
Доказательство.
Пусть
![]() и
и
![]() .
Тогда
.
Тогда
![]() и
и
![]() .
.
Если![]() или
или
![]() .■
.■
Замечание.
![]() определено только для многочленов
нулевой степени
определено только для многочленов
нулевой степени
![]() близко по свойствам к кольцу
близко по свойствам к кольцу
 алгоритм деления с остатком.
алгоритм деления с остатком.
3
o. Деление многочленов.
Теорема
2.
Пусть
![]() .
Тогда
.
Тогда
![]()
|
|
(1) |
Доказательство.
Пусть
![]() .
Если
.
Если
![]() ,
то можно положить
,
то можно положить
![]() .
Если
.
Если
![]() ,
то будем использовать тот же метод
деления, что и для чисел.
,
то будем использовать тот же метод
деления, что и для чисел.
Пусть
![]() и
и
![]() .
.
Положим
![]() .
Тогда
.
Тогда
![]() .
Пусть
.
Пусть
![]() и
и
![]()
.
Если
![]() ,
то остановим процесс вычисления; если
,
то остановим процесс вычисления; если
![]() ,
то положим
,
то положим
![]() .
.
Пусть
![]() ,
,
![]() – старший коэффициент
– старший коэффициент
![]() ,
и т.д. … Так как степени многочленов
,
и т.д. … Так как степени многочленов
![]() убывают, то получим
убывают, то получим
![]() :
:
![]()
и
![]() .
Процесс останавливается. Суммируя
полученные ранее выражения, получаем:
.
Процесс останавливается. Суммируя
полученные ранее выражения, получаем:
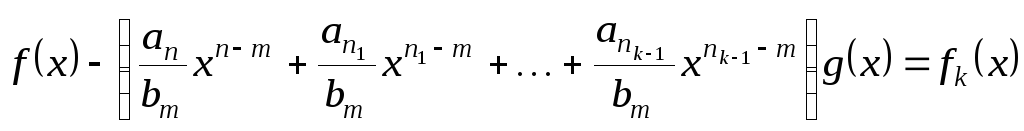 .
.
Тогда
![]() ,
,
![]() ,
т.е. получено требуемое представление
(1).
,
т.е. получено требуемое представление
(1).
Докажем единственность.
![]() Пусть
Пусть
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
Если
.
Если
![]()
, то
![]() (по
лемме 1)
(по
лемме 1)
![]() ,
a
,
a
![]() противоречие
противоречие
![]() .■
.■
Определение
2.
Если
![]() и
и
![]() ,
то
,
то
![]() называется остатком
при делении
называется остатком
при делении
![]() на
на
![]() .
.
Пример.
![]() .
.
Замечание.
Из указанного в теореме 2 алгоритма
деления с остатком следует, что если
![]() и
и
![]() – многочлены с действительными
коэффициентами, то коэффициенты всех
многочленов
– многочлены с действительными
коэффициентами, то коэффициенты всех
многочленов
![]() а значит и коэффициенты
а значит и коэффициенты
![]() и
и
![]() – действительные. Для целых коэффициентов
это утверждение, очевидно, неверно.
– действительные. Для целых коэффициентов
это утверждение, очевидно, неверно.
4o. Делители многочленов. Наибольший общий делитель.
Определение
3.
Пусть
![]() .
Если
.
Если
![]()
![]()
![]() ,
то говорят, что
,
то говорят, что
![]() делится на
делится на
![]() или
или
![]() делит
делит
![]() ,
и пишут
,
и пишут
![]() .
Если
.
Если
![]() , то
, то
![]() означает, что остаток от деления равен
означает, что остаток от деления равен
![]() .
В этом случае многочлен
.
В этом случае многочлен
![]() называется делителем
многочлена
называется делителем
многочлена
![]() .
.
Свойства
(делимости многочленов).
Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тогда справедливы свойства:
.
Тогда справедливы свойства:
1)
Если
![]() ,
,
![]() .
.
Доказательство
следует из равенства
![]() .
.
2)
![]() ,
,
![]()
![]()
![]() .
.
Доказательство. Так как
![]() ;
так как
;
так как
![]() .
Тогда имеем
.
Тогда имеем
![]() .
.
3)
![]() ,
,
![]()
![]()
![]() .
.
4)
![]()
![]()
![]()
![]() .
.
Доказательство.![]()
![]()
![]()
![]() .
Тогда
.
Тогда
![]() ;
следовательно,
;
следовательно,
![]() .
.
5)
Если
![]() ,
,
![]() ,
то справедливо
,
то справедливо
![]() .
.
6)
![]() .
.
Доказательство
следует из равенства
![]() .
.
7)
![]() имеем
имеем
![]() .
.
8)
![]() .
.
Действительно,
![]() .
.
9)
![]() .
.
Доказательство.
![]()
![]() и
и
![]() .
Ho
.
Ho
![]() .
.
![]() и
и
![]() .
.
10)
![]() .
.
Доказательство.
![]() Если
Если
![]() имеем
имеем
![]() .
.
Если
![]() и по свойству 1)
имеем
и по свойству 1)
имеем
![]() (в
силу свойства 9)
(в
силу свойства 9)
![]() .
.
![]() Следует из свойства
9.
Следует из свойства
9.
11) Если
![]() ,
то
,
то
![]() имеем
имеем
![]() .
.
Определение
4.
Многочлен
![]() называется общим
делителем
называется общим
делителем
![]() и
и
![]() ,
если
,
если
![]() и
и
![]() .
Наибольшим
общим делителем
(НОД) двух многочленов
.
Наибольшим
общим делителем
(НОД) двух многочленов
![]() и
и
![]() называется их делитель
называется их делитель
![]() ,
который делится на любой другой их общий
делитель.
,
который делится на любой другой их общий
делитель.
Замечание. Ненулевая постоянная является общим делителем любых двух многочленов.
Лемма
2.
Если НОД двух многочленов
![]() и
и
![]() существует, то он определен с точностью
до множителя
существует, то он определен с точностью
до множителя
![]() .
.
Доказательство.
Пусть
![]() и
и
![]() – два НОД для
– два НОД для
![]() и
и
![]()
![]() и
и
![]()
![]() (по
свойству 10)
(по
свойству 10)
![]() ,
для
,
для
![]() и
и
![]() .
.
Пусть
![]() .
Если
.
Если
![]() – общий делитель для
– общий делитель для
![]() и
и
![]() ,
то
,
то
![]() – тоже общий делитель. Если
– тоже общий делитель. Если
![]() –
НОД, т.е. любой другой делитель делит
–
НОД, т.е. любой другой делитель делит
![]() ,
то
,
то
![]() −
тоже
НОД.■
−
тоже
НОД.■
Лемма
3.
Если
![]() ,
,
![]() ,
то пары многочленов
,
то пары многочленов
![]() и
и
![]() имеют одинаковые общие делители.
имеют одинаковые общие делители.
Доказательство.
Пусть
![]() – общий делитель
– общий делитель
![]() и
и
![]()
![]() (из
(из
![]() )
)
![]() (по
свойству 5)
(по
свойству 5)
![]() .
Аналогично, из делимости
.
Аналогично, из делимости
![]() и
и
![]() на
на
![]()
![]()
![]() и
и
![]() делятся на
делятся на
![]() .■
.■
Лемма
4.
Если
![]() ,
то
,
то
![]() – НОД для
– НОД для
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
.
Доказательство
следует из того, что
![]() – делитель
– делитель
![]() и
и
![]() и любой делитель
и любой делитель
![]() и
и
![]() делит
делит
![]() .
.
Теорема
3. Для
![]() ,
,
![]()
![]() НОД(
НОД(![]() )
)![]() .
.
Доказательство.
Рассмотрим
![]() .
Если
.
Если
![]() ,
то в силу леммы 4 и условия
,
то в силу леммы 4 и условия
![]() имеем
имеем
![]() –
НОД(
–
НОД(![]() ).
).
Если![]() ,
то поделим
,
то поделим
![]() на
на
![]() с остатком
с остатком
![]() .
Если
.
Если![]()
![]() ,
то теорема доказана в силу леммы 4.
,
то теорема доказана в силу леммы 4.
Пусть
![]() .
Тогда делим
.
Тогда делим
![]() на
на
![]() .
Если остаток
.
Если остаток
![]() ,
то доказательство завершаем, если
,
то доказательство завершаем, если
![]() ,
то делим
,
то делим
![]() на
на
![]() и т.д. Так как степени остатков все время
уменьшаются, то процесс конечен. Таким
образом, имеем следующую последовательность
равенств:
и т.д. Так как степени остатков все время
уменьшаются, то процесс конечен. Таким
образом, имеем следующую последовательность
равенств:
|
|
|
|
|
|
|
|
|
|
|
(E) |
|
|
|
|
|
|
|
|
|
Здесь
![]() .
.
Из равенств (![]() )
и леммы 2
)
и леммы 2
![]() что
пары многочленов
что
пары многочленов
![]()
![]() имеют общие делители
имеют общие делители
![]() делители
делители
![]() и
и
![]() совпадают с делителями многочлена
совпадают с делителями многочлена
![]() (по
лемме 4)
(по
лемме 4)
![]()
![]() – делитель
– делитель
![]() и
и
![]() .
.
Если
![]() – любой другой делитель
– любой другой делитель
![]() и
и
![]()
![]() он
делитель и
он
делитель и
![]() – НОД.■
– НОД.■
Замечание 1. Алгоритм построения НОД, использованный в теореме 3, называется алгоритмом Евклида или алгоритмом последовательного деления.
Замечание
2. Если
![]()
![]() .
.
Замечание 3. Так как НОД определен с точностью до множителя, то будем считать, что коэффициенты при старшей степени равен 1.
Пример.
Если
![]()
![]() ,
то
,
то
![]() .
.
Замечание 4.
При вычислении НОД результаты вычисления
можно умножать и делить на элементы из
![]() ,
что влияет лишь на множители.
,
что влияет лишь на множители.
Теорема
4 (теорема
о разложении НОД). Пусть
![]() и
и
![]() ,
,
![]() .
Тогда
.
Тогда
![]()
|
|
(2) |
При этом, если
![]() ,
то
,
то
![]() и
и
![]() можно подобрать так, что
можно подобрать так, что
![]() и
и
![]() .
.
Доказательство.
Если
![]() ,
то
,
то
![]() .
.
Аналогично, если
![]() .
.
Пусть теперь
![]() и
и
![]() не является делителем
не является делителем
![]() .
Тогда можно считать, что
.
Тогда можно считать, что
![]() .
Из последнего равенства из (Е) следует,
что
.
Из последнего равенства из (Е) следует,
что
![]() .
.
Положим
![]()
![]() .
.
Из равенства
![]()
![]()
![]()
где
![]() .
.
Поднимаясь дальше вверх, приходим к (2).
Докажем второе
утверждение теоремы. Пусть (2) получено,
но
![]()
![]() Покажем, что (1) можно привести к виду
Покажем, что (1) можно привести к виду
![]()
где
![]()
Делим u
на g
с остатком:
![]() где
где
![]()
Подставим u в (1), имеем:
![]()
![]()
![]() (2)
(2)
Положим,
![]() .
Тогда
.
Тогда
![]() Покажем, что
Покажем, что
![]() От противного: пусть
От противного: пусть
![]() .
Имеем
.
Имеем
![]() Так как
Так как
![]() ,
что противоречит определению НОД.
,
что противоречит определению НОД.
Пример.
![]()
НОД
![]()
![]()
![]()
![]()
Замечание. Аналогично для случая многих многочленов вводится НОД.
5˚. Взаимно простые многочлены.
Определение
5.
Многочлены
![]() называют взаимно простыми, если их общие
делители только многочлены нулевой
степени.
называют взаимно простыми, если их общие
делители только многочлены нулевой
степени.
Лемма
5.
![]() –
взаимно просты
–
взаимно просты
![]() НОД
НОД
![]()
Теорема
5 (критерий
взаимной простоты многочленов)![]()
![]() −
взаимно просты
−
взаимно просты
![]()
![]()
Док-во:
![]()
![]() следует
из теоремы 4.
следует
из теоремы 4.
![]()
![]() Из (3)
Из (3)
![]() общий делитель
общий делитель
![]() и
и![]() должен
делить 1
должен
делить 1
![]() он постоянен
он постоянен
![]()
![]() - взаимно просты. ■
- взаимно просты. ■
Св-во (взаимно-простых многочленов)
1º.![]() - взаимно прост c
- взаимно прост c
![]() и
и![]()
![]() - взаимно прост с
- взаимно прост с
![]() .
.
Док-во:
НОД
![]() НОД
НОД
![]()
![]()
![]()
![]()
![]() |умножая
на
|умножая
на
![]() |
|
![]()
![]()
Если
![]() и
и
![]() - не взаимно просты
- не взаимно просты
![]()
![]() делитель, который является делителем
для
делитель, который является делителем
для
![]()
![]()
![]() - не взаимно просты . ■
- не взаимно просты . ■
2º.
![]() НОД
НОД
![]()
![]()
![]()
Док-во:
НОД
![]()
![]()
![]()
![]() |умножим на
|умножим на
![]() |
|
![]()
![]()
![]()
![]() .
Т.к.
.
Т.к.
![]() и
и
![]()
![]()
![]() ■
■
3º.
![]() НОД
НОД
![]()
![]()
![]()
Док-во:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ■
■
6º. Корни многочленов.
Определение
6.
Число
![]() называется корнем
называется корнем
![]() ,
если
,
если
![]()
Теорема 6 (теорема Безу).
![]() ,
тогда
,
тогда
![]()
![]()
![]()
Док-во:
Разделим
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ■
■
Замечание.
Остаток от деления
![]() по
по
![]() равен
равен
![]() .
.
![]()
Следствие. Число корней нулевого многочлена не превосходит его степени.
Док-во:
По индукции. Если
![]() ,
то
,
то
![]()
![]() корней нет
корней нет
![]() доказано.
доказано.
Пусть для
![]() доказано
и
доказано
и
![]()
Если нет корней
![]() все!
все!
Если
![]() - корень
- корень
![]() и
и
![]()
Корни
![]() - это корни
- это корни
![]() и наоборот
и наоборот
![]() (корни
(корни![]() )=(корни
)=(корни![]() )+1
)+1![]() .■
.■
Замечание. Т.о., задача нахождения корней многочлена равносильна нахождению его нормальных делителей.
Многочлен
![]() можно разделить на
можно разделить на
![]() с остатком используя так называемую
схему Горнера. Пусть
с остатком используя так называемую
схему Горнера. Пусть![]() имеет
вид:
имеет
вид:
![]()
и пусть
![]() где
где
![]() .
.
Приравнивая левую и правую часть, получаем:
![]()
![]()
![]()
![]() ,
,
![]() ,
…,
,
…,
![]() ,
,
![]() .
.
Откуда
![]()

Для практического использования схему Горнера строят следующим образом:
|
|
|
|
… |
|
… |
|
|
|
|
|
|
… |
|
… |
|
|
![]()
Отметим, что
![]()
Пример.
![]() Найти
Найти
![]()
|
|
1 |
0 |
-4 |
6 |
-8 |
10 |
|
2 |
1 |
|
-4+4=0 |
|
-8+12=4 |
|
Пусть с – корень
многочлена
![]() т.е.
т.е.
![]() и значит, по теореме Безу,
и значит, по теореме Безу,
![]() Может оказаться, что
Может оказаться, что
![]()
![]() ,
то
,
то
![]()
Определение
7.
Наибольшее
![]() называется кратностью корня
называется кратностью корня
![]() многочлена
многочлена
![]() корень
корень
![]() называется k-кратным
корнем
называется k-кратным
корнем
![]() Если k=1,
то корень называется простым.
Если k=1,
то корень называется простым.
Замечание1.
Если с – корень кратности k
для
![]() ,
то
,
то
![]() и
и
![]() т.е.
т.е.
![]() .
Наоборот, если
.
Наоборот, если
![]() и
и
![]() то с –корень кратности k
многочлена
то с –корень кратности k
многочлена
![]()
Предположим, что
![]()
![]()
![]()
![]()
![]() |
т.к. в кольце нет делителей нуля |
|
т.к. в кольце нет делителей нуля |
![]() противоречие.
противоречие.
Замечание2.
![]() является корнем нулевого многочлена.
является корнем нулевого многочлена.
Пусть
![]()
